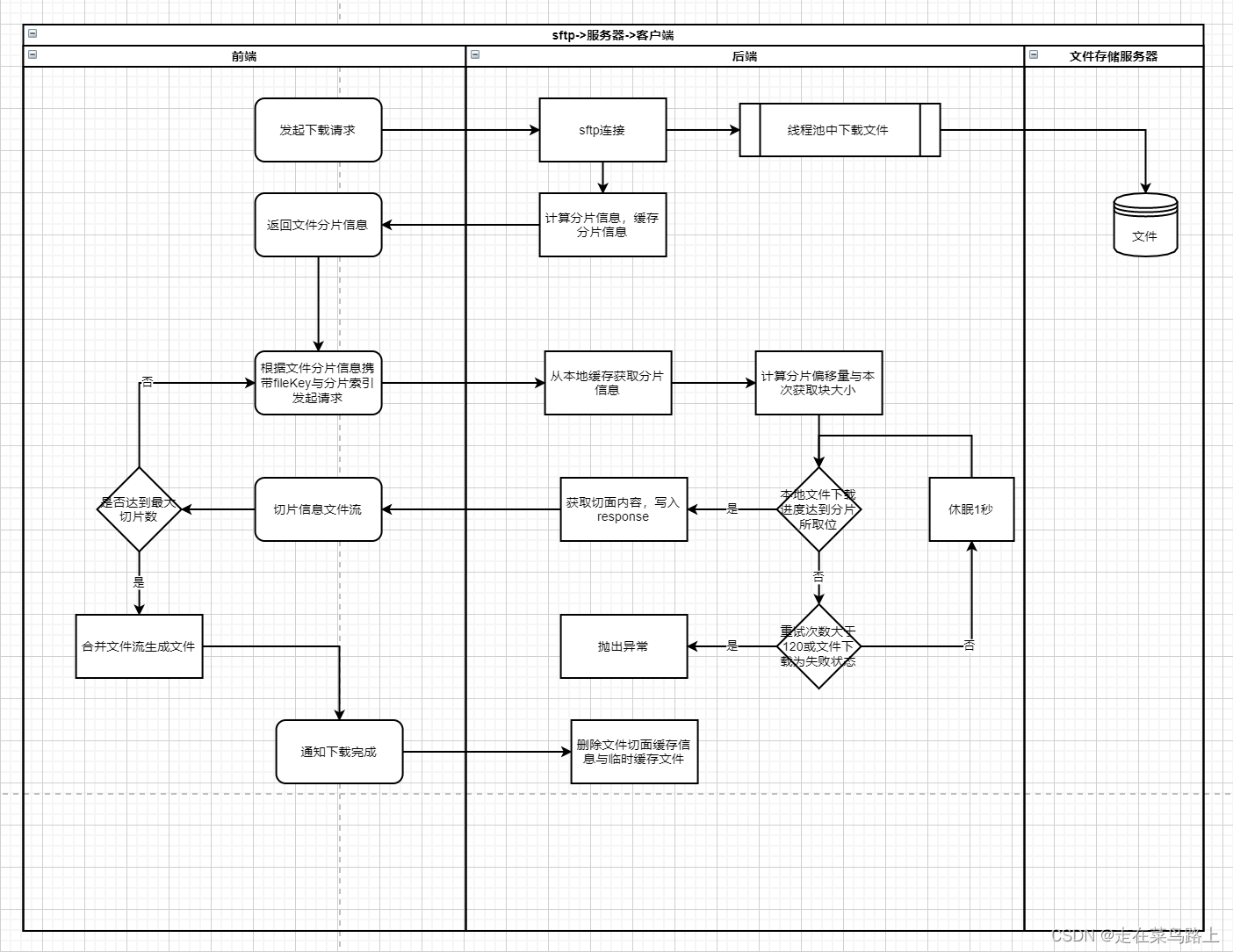
C#实现凸包算法之Jarvis
文章目录
- C#实现凸包算法之Jarvis
- 前言
- 示例代码
- 实现思路
- 测试结果
- 结束语
前言
这篇关于凸包算法的文章,本文使用C#和Jarvis算法来实现凸包算法。
首先消除两个最基本的问题:
- 什么是凸包呢?
凸包是一个包围一组点的凸多边形。凸多边形是指多边形中的每个内角都小于180度的多边形。 - 凸包算法有什么用呢?
凸包算法的作用是找到这个凸多边形,并且使用最少的点来绘制出它的轮廓。凸包算法在计算机图形学、计算几何和机器学习等领域中有着广泛的应用。
示例代码
现在来看一下C#中的Jarvis算法是如何实现凸包算法的:
/// <summary>
/// 通过Jarvis算法获取围绕所有点的凸多边形的轮廓点<br/>
/// </summary>
/// <param name="points">点数组</param>
/// <returns>轮廓点数组</returns>
public static PointD[] GetConvexHullByJarvis(PointD[] points)
{
if (points.Length < 3)
{
throw new ArgumentException("凸包算法需要至少3个点");
}
List<PointD> pointList = new List<PointD>(points);
// 找到最左边的点
PointD leftmostPoint = pointList[0];
for (int i = 1; i < pointList.Count; i++)
{
if (pointList[i].X < leftmostPoint.X)
{
leftmostPoint = pointList[i];
}
}
// 使用栈来存储凸包的点
Stack<PointD> hull = new Stack<PointD>();
PointD currentPoint = leftmostPoint;
do
{
hull.Push(currentPoint);
PointD endpoint = pointList[0];
for (int i = 1; i < pointList.Count; i++)
{
if (endpoint.Equals(currentPoint) || Cross(currentPoint, endpoint, pointList[i]) < 0)
{
endpoint = pointList[i];
}
}
currentPoint = endpoint;
pointList.Remove(currentPoint);
} while (!currentPoint.Equals(leftmostPoint));
return hull.ToArray();
}
上面代码中定义了一个名为GetConvexHullByJarvis的静态方法,该方法接受一个PointD类型的数组作为输入参数,并返回一个PointD类型的数组,表示围绕所有点的凸多边形的轮廓点。
补充一下,关于示例中使用到的Cross方法和PointD类型的源代码如下:
/// <summary>
/// 计算从 a 到 b 再到 c 的叉积
/// </summary>
/// <returns>叉积值</returns>
private static double Cross(PointD a, PointD b, PointD c)
{
return (b.X - a.X) * (c.Y - a.Y) - (b.Y - a.Y) * (c.X - a.X);
}
public struct PointD
{
public PointD(double x, double y)
{
X = x;
Y = y;
}
public double X { get; set; }
public double Y { get; set; }
public override bool Equals(object obj)
{
if (obj == null || GetType() != obj.GetType())
{
return false;
}
PointD other = (PointD)obj;
return X.Equals(other.X) && Y.Equals(other.Y);
}
}
实现思路
- 找到最左边的点,将它放入凸包中;
- 找到在当前点的右侧且离当前点最远的点,将它放入凸包中;
- 重复这个过程,直到回到最左边的点,形成一个闭合的凸多边形。
这就是 Jarvis 算法的基本思路。
需要注意的是,当点集中存在大量共线的点时,Jarvis 算法的时间复杂度可能会退化到 O(n^2) 级别,因为需要不断地扫描点集中的点来找到下一个点。此外当点集中存在大量重复的点时,Jarvis 算法可能会陷入死循环,因此需要对点集进行去重操作。
测试结果
用于测试的数据点:
static PointD[] points = new PointD[]
{
new PointD(0, 0),
new PointD(0, 10),
new PointD(10, 10),
new PointD(10, 0),
new PointD(1, 0),
new PointD(4, 3),
new PointD(5, 2),
new PointD(6, 5),
new PointD(4, 9),
new PointD(4, 2),
new PointD(5, 1),
new PointD(6, 5),
new PointD(1, 3),
new PointD(7, 2),
new PointD(8, 2),
new PointD(6, 7),
new PointD(8, 5),
new PointD(9, 3),
new PointD(7, 8),
new PointD(8, 9),
};
测试代码如下:
[TestMethod]
public void GetConvexHullByJarvis()
{
Console.WriteLine("Jarvis 算法");
PrintPoints(ConvexHull.GetConvexHullByJarvis(points));
}
private void PrintPoints(PointD[] points)
{
Console.WriteLine(points.Select(p => $" ({p.X}, {p.Y})").Join("\r\n"));
}
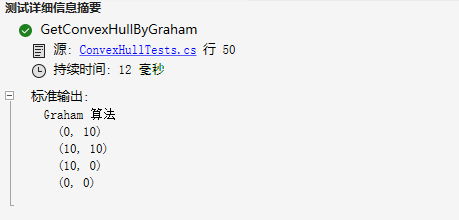
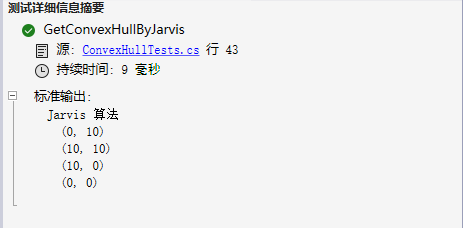
执行结果如下:
结束语
通过本章的代码可以轻松实现Jarvis算法并找到一组点最外侧的凸多边形。如果您觉得本文对您有所帮助,请不要吝啬您的点赞和评论,提供宝贵的反馈和建议,让更多的读者受益。