1 概述

Bayer转RGB在图像处理中被称为去马赛克（Demosaic），是机器视觉ISP流程中的一个基础且重要的算法，主要完成彩色图像传感器原始的Bayer格式图像到RGB格式图像的转换。

关于Bayer图像的相关概念和知识，本文不作介绍。常见知识点以及各种Bayer转RGB算法的介绍网上有很多博文可以参考学习：

https://www.cnblogs.com/qiqibaby/p/5267566.html

三种Bayer数据的插值算法（CCD插值算法）_bayer插值_simple_96的博客-CSDN博客

https://www.cnblogs.com/qiqibaby/p/8719252.html

https://www.cnblogs.com/sunny-li/p/8641767.html

http://www.voidcn.com/article/p-zeuhnrel-ww.html

Bayer转RGB的核心思想就是色彩插值。各种不同算法主要目的都是真实还原图像的色彩，并解决物体边缘、色彩变化处出现的拉链效应和色彩混叠现象。

2 基于梯度校正的线性插值法

Bayer转RGB的算法有很多种，很多算法在插值过程中都会考虑领域色彩的梯度，根据梯度对插值结果进行补偿或校正。考虑到在FPGA中实现的效果和资源使用问题，选取了一种经典的算法：gradient-corrected linear interpolation，出自微软研究院，该算法被matlab中的demosaic函数所使用。

算法论文链接：http://research.microsoft.com/pubs/102068/Demosaicing_ICASSP04.pdf

该算法的主要原理为：在5*5大小的窗口中，利用中心点像素所属颜色的梯度值对其它颜色的插值结果进行补偿。其中，R和B都考虑了上下左右4个方向的梯度；G除了上下左右4个方向，还考虑了4个对角线方向的梯度，这应该是由于G的像素点个数是R和B的2倍，而且人眼对于绿色的敏感度更强。

一共有8种情况，4种计算公式。如下图所示：

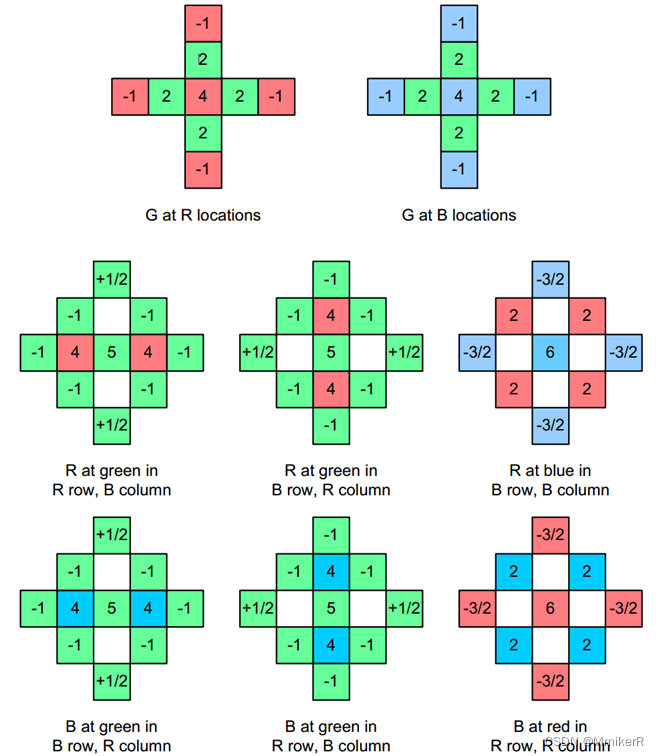
4种顺序的bayer阵列对应的R、G、B插值方式如下图所示：

算法对应的matlab程序为：

function out=bayer_to_rgb(in) 
m=size(in,1);n=size(in,2); 
 
outR=in; 
outG=in; 
outB=in; 
 
%rg 
%gb 
for i=3:2:m-3 
    for j=3:2:n-3 
        outR(i,j)=in(i,j)*8; 
        outG(i,j)=(in(i-1,j)+in(i,j-1)+in(i,j+1)+in(i+1,j))*2-(in(i-2,j)+in(i+2,j)+in(i,j-2)+in(i,j+2))+in(i,j)*4; 
        outB(i,j)=(in(i-1,j-1)+in(i-1,j+1)+in(i+1,j-1)+in(i+1,j+1))*2-(in(i-2,j)+in(i,j-2)+in(i,j+2)+in(i+2,j))*3/2+in(i,j)*6; 
    end 
end 
 
%gr 
%bg 
for i=3:2:m-3 
    for j=4:2:n-2 
        outR(i,j)=in(i,j-1)*4+in(i,j+1)*4+(in(i-2,j)+in(i+2,j))/2-(in(i-1,j-1)+in(i-1,j+1)+in(i+1,j-1)+in(i+1,j+1)+in(i,j-2)+in(i,j+2))+in(i,j)*5; 
        outG(i,j)=in(i,j)*8; 
        outB(i,j)=(in(i-1,j)+in(i+1,j))*4-(in(i-2,j)+in(i-1,j-1)+in(i-1,j+1)+in(i+1,j-1)+in(i+1,j+1)+in(i+2,j))+(in(i,j-2)+in(i,j+2))/2+in(i,j)*5; 
    end 
end
 
%gb 
%rg 
for i=4:2:m-2 
    for j=3:2:n-3 
        outR(i,j)=(in(i-1,j)+in(i+1,j))*4-(in(i-2,j)+in(i-1,j-1)+in(i-1,j+1)+in(i+1,j-1)+in(i+1,j+1)+in(i+2,j))+(in(i,j-2)+in(i,j+2))/2+in(i,j)*5; 
        outG(i,j)=in(i,j)*8; 
        outB(i,j)=(in(i,j-1)+in(i,j+1))*4-(in(i-1,j-1)+in(i-1,j+1)+in(i,j-2)+in(i,j+2)+in(i+1,j-1)+in(i+1,j+1))+(in(i-2,j)+in(i+2,j))/2+in(i,j)*5; 
    end 
end 
 
%bg 
%gr 
for i=4:2:m-2 
    for j=4:2:n-2 
        outR(i,j)=(in(i-1,j-1)+in(i-1,j+1)+in(i+1,j-1)+in(i+1,j+1))*2-(in(i-2,j)+in(i,j-2)+in(i,j+2)+in(i+2,j))*3/2+in(i,j)*6; 
        outG(i,j)=(in(i-1,j)+in(i,j-1)+in(i,j+1)+in(i+1,j))*2-(in(i-2,j)+in(i,j-2)+in(i,j+2)+in(i+2,j))+in(i,j)*4; 
        outB(i,j)=in(i,j)*8; 
    end 
 
end 

out(:,:,1)=outR/8; 
out(:,:,2)=outG/8; 
out(:,:,3)=outB/8;

原始bayer图：