动态规划2:题目

news2024/12/23 9:57:14

目录

第1题 Fibonacci

第2题 字符串分割(Word Break)

.第3题 三角矩阵(Triangle)

第4题 路径总数(Unique Paths)

第5题 最小路径和(Minimum Path Sum)

第6题 背包问题

第7题 回文串分割(Palindrome Partitioning)

第8题 编辑距离(Edit Distance)

第9题 不同子序列(Distinct Subsequences)

第1题 Fibonacci

分析问题:

1. 状态定义F(i):第i个项的值

2. 状态间的转移方程定义:F(i)=F(i-1)+F(i-2)

3. 状态的初始化:F(0)=0 F(1)=1

4. 返回结果:F(i)

public class Solution {
    public int Fibonacci(int n) {
        //创建数组,保存状态的值
        int[] dp=new int[n+1];
        dp[0]=0;
        dp[1]=1;
        //F(i)=F(i-1)+F(i-2)
        //从第二个开始到第n个结束
        for(int i=2;i<=n;i++){
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];

    }
}

第2题 字符串分割(Word Break)

F(i)   F(j) && [j+1,i]  可以在词典中找到

分析问题:

1. 状态定义F(i):

       字符串s是否可以分割

2. 状态间的转移方程定义:

        F(i):(j<i) && F(j) $$ [j+1,i] 是否可以在词典中找到

3. 状态的初始化:

             F(0)=true

4. 返回结果:

        F(字符串长度):f(s.size())

public class Solution {
    public boolean wordBreak(String s, Set<String> dict) {
       boolean[] dp=new boolean[s.length()+1];
       dp[0]=true;
       for(int i=1;i<=s.length();i++){
        for(int j=0;j<i;j++){
            if(dp[j] && dict.contains(s.substring(j,i))){
                dp[i]=true;
                break;
            }
        }
        
       }
       return dp[s.length()];
       
    }
}

.第3题 三角矩阵(Triangle)

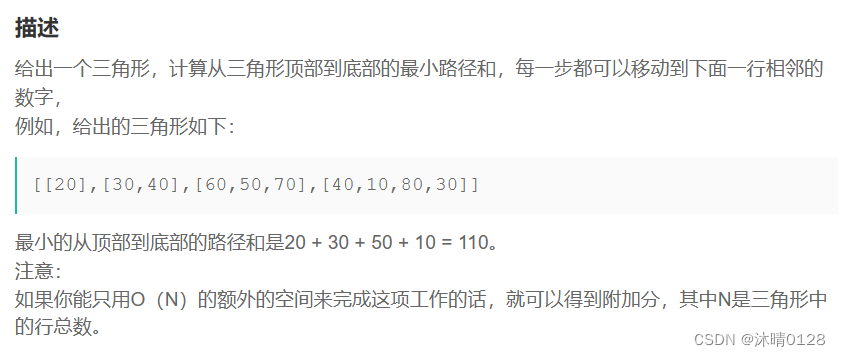
问题:从顶部到底部的最小路径和

状态:从(0,0)到(i,j)的最小路径和

状态转移方程:

(0

F(i,j): min(F(i-1,j-1),F(i-1,j))+array[i][j] 前一个最小的和当前的值的和

(j==0 || j==i):F(i,j):

j==0 ; (F(i-1,0)+array[i][0]

j==i;F(i-1,j-1)+array[i][j]

初始状态:

F(0,0)=array[0][0]

返回结果:

min(F(row-1,j))

public int minimumTotal(ArrayList<ArrayList<Integer>> triangle) {
    if(triangle.isEmpty()){
        return 0;
    }

    List<List<Integer>> minPathSum=new ArrayList<>();
    for(int i=0;i<triangle.size();i++){
        minPathSum.add(new ArrayList<>());
    }
    //F(0)(0)初始化
    minPathSum.get(0).add(triangle.get(0).get(0));
    for(int i=1;i<triangle.size();i++){
        int curSum=0;
        for(int j=0;j<=i;j++){
            if(j==0){
                curSum=minPathSum.get(i-1).get(0);
            }
            else if(j==i){
                curSum=minPathSum.get(i-1).get(j-1);
            }else{
                curSum=Math.min(minPathSum.get(i-1).get(j),minPathSum.get(i-1).get(j-1));
            }
            //之前的值加当前的值
            minPathSum.get(i).add(triangle.get(i).get(j)+curSum);
        }
    }
    int size=triangle.size();
    //值为最后一行第一个
    int allMin=minPathSum.get(size-1).get(0);
    for (int i = 1; i < size; i++) {
        //遍历最后一行找到最小值
        allMin=Math.min(allMin,minPathSum.get(size-1).get(i));
    }
    return allMin;
}

第4题 路径总数(Unique Paths)

 

状态:从(0,0)到任意一点的个数

转移方程:F(i,i)=F(i-1,j)+F(i,j-1);   上面和左面的个数和

初识状态:F(i,0)=F(0,j)=1;

返回结果: F(m-1,n-1)

 public int uniquePaths (int m, int n) {
       int[][] arr=new int[m][n];
       //初始化
       for(int i=0;i<m;i++){
        arr[i][0]=1;
       }
       for(int i=0;i<n;i++){
        arr[0][i]=1;
       }
       //过程
       for(int i=1;i<m;i++){
        for(int j=1;j<n;j++){
            arr[i][j]=arr[i-1][j]+arr[i][j-1];
        }
       }
       return arr[m-1][n-1];
    }

第5题 最小路径和(Minimum Path Sum)

状态: 从(0,0)到(i,j)的最短路径和

状态转移方程:F(i,j)=min{F(i-1,j),,F(i,j-1)}+array[i][j]

                       i==0   F=F(0,j-1)+array[0][j]

                         j==0 F(i-1,0)+array[i][j]

初始化   F(0,0)=array[0][0]

返回结果:F(m-1,n-1)

public int minPathSum (int[][] grid) {
       
       int n=grid.length;
       int m=grid[0].length;
       if(n==0 || m==0){
        return 0;
       }
       //在grid的基础上改
       for(int i=1;i<n;i++){
        grid[i][0]=grid[i-1][0]+grid[i][0];
       }
       for(int i=1;i<m;i++){
        grid[0][i]=grid[0][i-1]+grid[0][i];
       }
       for(int i=1;i<n;i++){
        for(int j=1;j<m;j++){
            grid[i][j]=Math.min(grid[i-1][j],grid[i][j-1])+grid[i][j];
        }
       }
       return grid[n-1][m-1];

    }

第6题 背包问题

 

状态:F(i,j):从前I个商品中选择,包的大小为j时,最大值

状态转移方程:

      1.能放入:

                1.不放:和前一个相同

                 2.放入:大小剪去改商品的大小,价值增加

      2.不能放入: 

               和前一个相同

初识状态:

         第0行和第0列都为0,表示 没有商品或者包大小为0

       F(0,j)=F(i,0)=0;

     返回结果F(m,n)

 public int backPackII(int m, int[] a, int[] v) {
        //得到商品总个数
        //包大小为0,或没有商品直接返回
        //创建二维数组:表示背包总价值   列表示放入的商品个数  行表示包的大小
        //初始化  行为0,或列为0,结果都为0
        //过程  判断商品大小,有放入和不放入两种
        //返回
        int num=a.length;
        if(m==0 || num==0){
            return 0;
        }
          // 0,0返回,所以要+1
        int[][] dp=new int[num+1][m+1];
        for(int i=0;i<=num;i++){
            dp[i][0]=0;
        }
        for(int i=0;i<=m;i++){
            dp[0][i]=0;
        }
      //从1到num开始遍历
        for(int i=1;i<=num;i++){
            for(int j=1;j<=m;j++){
               //a,v数组是从0开始的
               //dp从1开始
                if(a[i-1]>j){
                    dp[i][j]=dp[i-1][j];
                }else{
                    int cur=dp[i-1][j-a[i-1]]+v[i-1];
                    dp[i][j]=Math.max(cur,dp[i-1][j]);
                }
            }
        }
        return dp[num][m];

第7题 回文串分割(Palindrome Partitioning)

  如果从j+1到i为回文串,也知道j之前的分割次数,就在切一次,保证都是回文串

       F(i):[i,i]是回文串:0

              j<i && [j+1][i]是回文串:min(f(i)+1)

 

状态:f(i):s的前i个字符最小的分割次数

状态转移方程:

    如果j到i-1是是回文串,f(j)+1

F(i,j):

初始状态:

        f(i)=i-1  从1开始  最大分割次数为每一个字母都分割一次

循环判断首尾元素是否相同，如果全部相同，则是回文串

import java.util.*;


public class Solution {
    /**
     * 
     * @param s string字符串 
     * @return int整型
     */
 public int minCut (String s) {
    int len=s.length();
    if(len==0){
        return 0;
    }
    int[] minCut=new int[len+1];
    //初始化
    for(int i=0;i<=len;i++){
        minCut[i]=i-1;
    }
    for (int i = 1; i <=len ; i++) {
        for (int j = 0; j <=i ; j++) {
            //前面的循环就直接可以拿到0-j是不是回文串的结果
            //前面的结果是已知的,要判断后面的是不是回文串
            if(isPal(s,j,i-1)){
                minCut[i]=Math.min(minCut[i],minCut[j]+1);
            }
        }
    }
    return minCut[len];
    
}

private boolean isPal(String s, int start, int end) {
    while(start<end){
        if(s.charAt(start)!=s.charAt(end)){
            return false;
        }
        start++;
        end--;
    }
    return true;
}
}

第8题 编辑距离(Edit Distance)

 

问题:word1到word2的编辑距离

子问题:word1局部到word2局部的编辑距离

状态：

F(i,j):word1前i个字符到word2前j个字符的编辑距离

min(删除,插入,替换(相等不加一))

F(i,j) = min { F(i-1,j）+1, F(i,j-1) +1, F(i-1,j-1) +(w1[i]==w2[j]?0:1) }

                      i删除             增加i           如果i,j对应的字符相等,不操作,如果不相等,+1

初始化:F(i,0)=i

            F(0,i)=i

返回结果:F(m,n)

步骤:

  1. 有一个为空,返回另一个的长度
  2. 初始化   
  3. 状态变化:从1开始
    1. 得到插入和删除的最小值
    2. 判断i,j对应的元素是否相等
    3. 替换和1得到的值取最小值
  4. 返回
import java.util.*;


public class Solution {
    /**
     * 
     * @param word1 string字符串 
     * @param word2 string字符串 
     * @return int整型
     */
     public int minDistance (String word1, String word2) {
        // write code here
        if(word1.isEmpty() || word2.isEmpty()){
            return Math.max(word1.length(),word2.length());
        }
        int row=word1.length();
        int col=word2.length();
        int[][] dp=new int[row+1][col+1];
        for(int i=0;i<=row;i++){
            dp[i][0]=i;
        }
        for(int i=0;i<=col;i++){
            dp[0][i]=i;
        }
        for(int i=1;i<=row;i++){
            for(int j=1;j<=col;j++){
                int cur=Math.min(dp[i-1][j],dp[i][j-1])+1;
                if(word1.charAt(i-1) ==word2.charAt(j-1)){
                    dp[i][j]=Math.min(dp[i-1][j-1],cur);
                }else{
                    dp[i][j]=Math.min(dp[i-1][j-1]+1,cur);
                }
            }
        }
        return dp[row][col];
    }
}

第9题 不同子序列(Distinct Subsequences)

 

  1. 问题:
    1. S中和T相同的子序列的个数
  2. 子问题:
    1. S的子串中和T相同的子序列的个数
  3. 状态F(i):
    1. S的前i个字符构成的子串中和T相同的子序列的个数
    2. 子串长度>=T的长度
    3. 在F(i,j)处需要考虑S[i] = T[j] 和 S[i] != T[j]两种情况
  4. 状态转移方程
    1. 当s[i]!=T[j]:   F(i,j)=F(i-1,j)
    2. 当s[i]==T[i]:
      1. 匹配: F(i,j)=F(i-1,j-1)
      2. 不匹配: F(i,j)=F(i-1,j)     s,t下标从0开始
  5. 初始化:
    1. F(i,0)=1  s中包含空集
    2. F(0,j)=0  空集中不包含
import java.util.*;


public class Solution {
    /**
     * 
     * @param S string字符串 
     * @param T string字符串 
     * @return int整型
     */
   public int numDistinct (String S, String T) {
        int slen=S.length();
        int tlen=T.length();
        //初始化
        int[][] dp=new int[slen+1][tlen+1];
        dp[0][0]=1;
        for(int i=1;i<=slen;i++){
            dp[i][0]=1;
        }
        for(int i=1;i<=tlen;i++){
            dp[0][i]=0;
        }
        for(int i=1;i<=slen;i++){
            for(int j=1;j<=tlen;j++){
                if(S.charAt(i-1)==T.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
                }else{
                    dp[i][j]=dp[i-1][j];
                }
            }
        }
        return dp[slen][tlen];
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/579910.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Dubbo入门案例

Dubbo入门案例

1.基于以下图实现服务 提供者、消费者 2.前期工作 父POM <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLo…
阅读更多...
如何在本地安装多个nodejs版本，方便前端开发

如何在本地安装多个nodejs版本，方便前端开发

目录 &#x1f4dd;一&#xff0c;使用 nvm&#xff08;Node Version Manager&#xff09;: &#x1f4dd;二&#xff0c;使用 n&#xff08;Node.js 版本管理器&#xff09;: &#x1f4e2;要在本地安装多个 Node.js 版本以便于前端开发&#xff0c;你可以使用工具如 nvm&am…
阅读更多...
js常用事件

js常用事件

js常用事件如下&#xff1a; onmouseover&#xff1a;鼠标被移到某元素之上&#xff1b; onmouseout&#xff1a;鼠标从某元素移开&#xff1b; onfocus&#xff1a;元素获得焦点&#xff1b; onblur&#xff1a;元素失去焦点&#xff1b; onclick&#xff1a;鼠标单击事件…
阅读更多...
蓝桥杯嵌入式STM32G431RBT6竞赛指南与模板——最后的绝唱

蓝桥杯嵌入式STM32G431RBT6竞赛指南与模板——最后的绝唱

谨以此文和我去年前的一篇蓝桥杯单片机的教程构成电子类的青铜双壁. 国信长天单片机竞赛训练之原理图讲解及常用外设原理&#xff08;遗失的章节-零&#xff09;_昊月光华的博客-CSDN博客 目录 时钟树 串口重定向&#xff1a;printf输出 动态点灯(点灯大师) 按键(常用状态…
阅读更多...
RabbitMQ学习-发布确认高级

RabbitMQ学习-发布确认高级

发布确认springboot版本 确认机制方案&#xff1a; 代码架构图&#xff1a; 配置文件&#xff1a; 在application.properties全局配置文件中添加spring.rabbitmq.publish-confirm-type属性&#xff0c;这个属性有以下几种值 none:禁用发布确认模式(默认)0 correlated:发布消…
阅读更多...
Redis的SDS+IntSet+Dict

Redis的SDS+IntSet+Dict

一)SDS 在redis中&#xff0c;保存key的是字符串&#xff0c;value往往是字符串或者是字符串的集合&#xff0c;可见字符串是redis中最常用的一种数据结构: 但是在redis中并没有直接使用C语言的字符串&#xff0c;因为C语言的字符串存在很多问题 1)获取字符串的长度需要通过运算…
阅读更多...
算法12.从暴力递归到动态规划5

算法12.从暴力递归到动态规划5

算法|12.从暴力递归到动态规划5 1.机器人行进问题 题意&#xff1a;假设有排成一行的N个位置记为1~N&#xff0c;N一定大于或等于2 开始时机器人在其中的M位置上(M一定是1~N中的一个) 如果机器人来到1位置&#xff0c;那么下一步只能往右来到2位置&#xff1b; 如果机器人来到…
阅读更多...
stc15w404as使用keil做库，提供头文件，供调用

stc15w404as使用keil做库，提供头文件，供调用

背景 有个项目使用需要使用库&#xff0c;将代码封装起来&#xff0c;仅仅留下调试接口&#xff0c;给用户使用&#xff0c;调试一些参数。这样工程看起来更简单&#xff0c;也方便客户维护。 也有一些使用场景&#xff0c;需要把自己的代码封装起来&#xff0c;这个是怕被别…
阅读更多...
电脑msvcp120.dll缺失怎么办？由于找不到msvcp120.dll的解决方案

电脑msvcp120.dll缺失怎么办？由于找不到msvcp120.dll的解决方案

MSVCP120.dll文件是Windows操作系统中的一种动态链接库文件。它是由Microsoft C软件包提供的重要组件。当系统提示“MSVCP120.dll文件缺失”时&#xff0c;可能会导致某些应用程序无法正常运行。 以下是修复MSVCP120.dll缺失问题的几种方法&#xff1a; 方法一&#xff1a;修复…
阅读更多...
如何在华为OD机试中获得满分？Java实现【公共子串计算】一文详解！

如何在华为OD机试中获得满分？Java实现【公共子串计算】一文详解！

✅创作者&#xff1a;陈书予 &#x1f389;个人主页&#xff1a;陈书予的个人主页 &#x1f341;陈书予的个人社区&#xff0c;欢迎你的加入: 陈书予的社区 &#x1f31f;专栏地址: Java华为OD机试真题&#xff08;2022&2023) 文章目录 1、题目描述2、输入描述3、输出描述…
阅读更多...
＜学习笔记＞从零开始自学Python-之-web应用框架Django（ 十四）上线部署（阿里云+Nginx+uwsgi+MySQL）

＜学习笔记＞从零开始自学Python-之-web应用框架Django（ 十四）上线部署（阿里云+Nginx+uwsgi+MySQL）

好了&#xff0c;我们现在有了一个完整的网站&#xff0c;在自己电脑上跑起来没问题了&#xff0c;但是我们做网站肯定不只是为了在本机上自己欣赏&#xff0c;总要放到网上去让别人来浏览。这一章我们就完整跑一遍Django项目的生产环境部署。 1、基本原理 想让你的网站在公网…
阅读更多...
【P38】JMeter 随机控制器（Random Controller）

【P38】JMeter 随机控制器（Random Controller）

文章目录 一、随机控制器&#xff08;Random Controller&#xff09;参数说明二、测试计划设计2.1、测试计划一2.2、测试计划二2.3、勾选忽略子控制器块 一、随机控制器&#xff08;Random Controller&#xff09;参数说明 可以让控制器内部的逻辑随机执行一个&#xff0c;一般…
阅读更多...
如何在华为OD机试中获得满分？Java实现【24点游戏算法】一文详解！

如何在华为OD机试中获得满分？Java实现【24点游戏算法】一文详解！

✅创作者&#xff1a;陈书予 &#x1f389;个人主页&#xff1a;陈书予的个人主页 &#x1f341;陈书予的个人社区&#xff0c;欢迎你的加入: 陈书予的社区 &#x1f31f;专栏地址: Java华为OD机试真题&#xff08;2022&2023) 文章目录 1、题目描述2、输入描述3、输出描述…
阅读更多...
python自动演奏Freepiano【双手合奏】

python自动演奏Freepiano【双手合奏】

文章编写背景 玩了N久的Freepiano,碍于本人没有天赋&#xff0c;左右手一直没法协调。 于是&#xff0c;突然奇想&#xff0c;也是代码设计的思路&#xff1a; 用多线程的方式&#xff0c;开两个线程&#xff0c;然后通过按键模拟的方式&#xff0c;分别模拟左右手去演奏。觉…
阅读更多...
分布式网络通信框架（一）——集群和分布式

分布式网络通信框架（一）——集群和分布式

单机聊天服务器 缺点&#xff1a; 受限于硬件资源&#xff0c;服务器所能承受的用户并发量不够大&#xff1b; 任意模块修改&#xff0c;都会导致整个项目代码重新编译、部署&#xff1b; 系统中&#xff0c;有些模块是CPU密集型&#xff0c;有些是IO密集型&#xff0c;造成…
阅读更多...
计算机网络五 传输层

计算机网络五 传输层

传输层 概念 传输层是指ISO/OSI模型中的第四层&#xff0c;在计算机网络中起着非常重要的作用。它负责数据在网络中的传输&#xff0c;管理数据传输的可靠性和流量控制&#xff0c;保证数据在网络中不会丢失或重复。 提供的服务 传输层提供的主要服务有两种&#xff0c;分别…
阅读更多...
《数据库应用系统实践》------ 包裹信息管理系统

《数据库应用系统实践》------ 包裹信息管理系统

系列文章 《数据库应用系统实践》------ 包裹信息管理系统 文章目录 系列文章一、需求分析1、系统背景2、 系统功能结构&#xff08;需包含功能结构框图和模块说明&#xff09;3&#xff0e;系统功能简介 二、概念模型设计1&#xff0e;基本要素&#xff08;符号介绍说明&…
阅读更多...
9. Linux下实现简单的UDP请求

9. Linux下实现简单的UDP请求

本文简单介绍了UDP传输层协议&#xff0c;并在Linux下实现简单的socket通讯 一、UDP UDP&#xff08;User Datagram Protocol&#xff0c;用户数据报协议&#xff09;是一种无连接的传输层协议&#xff0c;它不保证数据包的可靠性和顺序。UDP在IP协议的基础上增加了简单的差错…
阅读更多...
阿里云服务器配置CPU内存、带宽和系统盘选择方法

阿里云服务器配置CPU内存、带宽和系统盘选择方法

阿里云服务器配置怎么选择&#xff1f;CPU内存、公网带宽和系统盘怎么选择&#xff1f;个人用户选择轻量应用服务器或ECS通用算力型u1云服务器&#xff0c;企业用户选择ECS计算型c7、通用型g7云服务器&#xff0c;阿里云服务器网分享阿里云服务器配置选择方法&#xff1a; 目录…
阅读更多...
大数据周会-本周学习内容总结015

大数据周会-本周学习内容总结015

开会时间&#xff1a;2023.05.28 15:30 线下会议 目录 01【fhzny项目】 02【Spark】 03【调研-数仓构建】 3.1【数仓构建&#xff0c;流程图、架构图、使用场景】 场景选择 组件设计 构建流程 04【专利】 05【导师点评】 01【fhzny项目】 GitLabMyBatis-PlusSpringbo…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023