一、题目
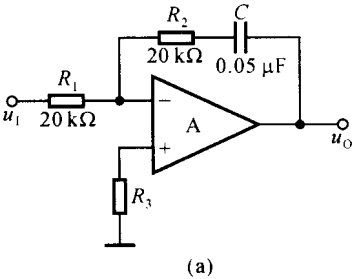
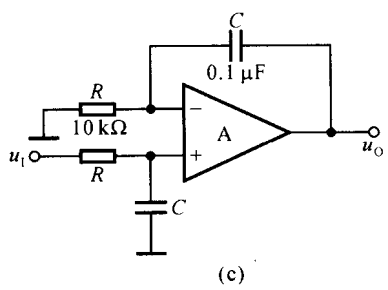
利用 Multisim 分析图1所示两个积分运算电路的输出波形,输入电压为 200 Hz、幅值为 ± 1 V 的方波信号。
|
|
图 1 图1\,\, 图1
二、仿真电路
在 Multism 中搭建图1所示的两个电路,如图2所示。为了防止电路中的直流增益过大,故在电容上并联上 1MΩ 的电阻。
 图
2
积分运算电路
图2\,\,积分运算电路
图2积分运算电路
图
2
积分运算电路
图2\,\,积分运算电路
图2积分运算电路
三、理论分析
可以求得图1(a)、( c c c) 所示电路输出电压与输入电压的运算关系为 ( a ) u O = − R 2 R 1 u I − 1 R 1 C ∫ u I d t = − u I − 1000 ∫ u I d t (a)\,\,u_{\scriptscriptstyle O}=-\frac{R_2}{R_1}u_{\scriptscriptstyle I}-\frac{1}{R_1C}\int u_{\scriptscriptstyle I}\textrm dt=-u_{\scriptscriptstyle I}-1000\int u_{\scriptscriptstyle I}\textrm dt (a)uO=−R1R2uI−R1C1∫uIdt=−uI−1000∫uIdt ( c ) u O = 1 R C ∫ u I d t = 1000 ∫ u I d t (c)\,\,u_{\scriptscriptstyle O}=\frac{1}{RC}\int u_{\scriptscriptstyle I} \textrm dt=1000\int u_{\scriptscriptstyle I}\textrm dt\kern 80pt (c)uO=RC1∫uIdt=1000∫uIdt电路(a)实现积分求和运算,它利用 R 2 R_2 R2 与 C C C 串联实现求和运算,电阻上电压与输入电压的比例系数为 − R 2 / R 1 -R_2/R_1 −R2/R1。电路(c)实现同相积分运算。
四、仿真结果
仿真的波形如图3所示。

图
1
(
a
)
电路仿真波形
图1(a)电路仿真波形
图1(a)电路仿真波形 图
1
(
c
)
电路仿真波形
图1(c)电路仿真波形
图1(c)电路仿真波形
图
3
输出信号波形
图3\,\,输出信号波形
图3输出信号波形
图
1
(
c
)
电路仿真波形
图1(c)电路仿真波形
图1(c)电路仿真波形
图
3
输出信号波形
图3\,\,输出信号波形
图3输出信号波形
五、仿真数据
仿真结果的主要数据如表1所示。 表 1 积分运算电路的仿真数据 表1\,\,积分运算电路的仿真数据 表1积分运算电路的仿真数据
| 电路 | 图1(a) | 图1( c c c) |
|---|---|---|
| T 1 T_1 T1时刻电压 / V | 2.209 | -1.253 |
| T 2 T_2 T2时刻电压 / V | -2.206 | 1.244 |
| 说明 | 因集成运放的非理想性,实测值与理论值存在误差 | 理想情况下两个时刻的数值应相等 |
六、结论
(1)图1(a) 实现了反相积分求和,其为输出积分叠加上了输入方波的直流信号;图1(
c
c
c)实现了同相积分运算电路。
(2)因集成运放非理想性,输出信号的正负时刻的电压数值存在误差。

![[Nacos] Nacos Server处理订阅请求 (九)](https://img-blog.csdnimg.cn/defdfab6f1944a388340ff063ffce63a.png)