假设检验的核心其实就是反证法。反证法是数学中的一个概念，就是你要证明一个结论是正确的，那么先假设这个结论是错误的，然后以这个结论是错误的为前提条件进行推理，推理出来的结果与假设条件矛盾，这个时候就说明这个假设是错误的，也就是这个结论是正确的。以上就是反证法的一个简单思路。

了解完反证法以后，我们开始正式的假设检验，这里还是引用一个大家都很熟悉的一个例子『女士品茶』。

女士品茶是一个很久远的故事，讲述了在很久很久以前的一个下午，有一群人在那品茶，这个时候有位女士提出了一个有趣的点，就是把茶加到奶里和把奶加到茶里面最后得到的『奶茶』的味道是不一样的。大部分人都觉得这位女士在瞎说，只有其中一位男士提出了要用科学的方法去证明到底一样不一样(牛人想问题角度永远都是那么独特，多想想别人为什么那么说，而不是一上来就不经思考的拒绝)。

接下来，我们具体看一下这一位男士是怎么去证明的。首先他假设了把茶加到奶里和把奶加到茶里面得出来的『奶茶』味道是一样的。然后随机把这两种『奶茶』端给女士，让女士品，是先加的奶还是先加的茶，如果女士都能品对，说明确实有差异，如果要是品不对，说明是没差异的。这里面就涉及到一个问题，让女士品多少杯呢，品一杯肯定是不行的，因为任意一杯猜对(瞎蒙)的概率都有50%。下面是不同杯数对应的猜对的概率(注意，这里是猜对而不是品对)。

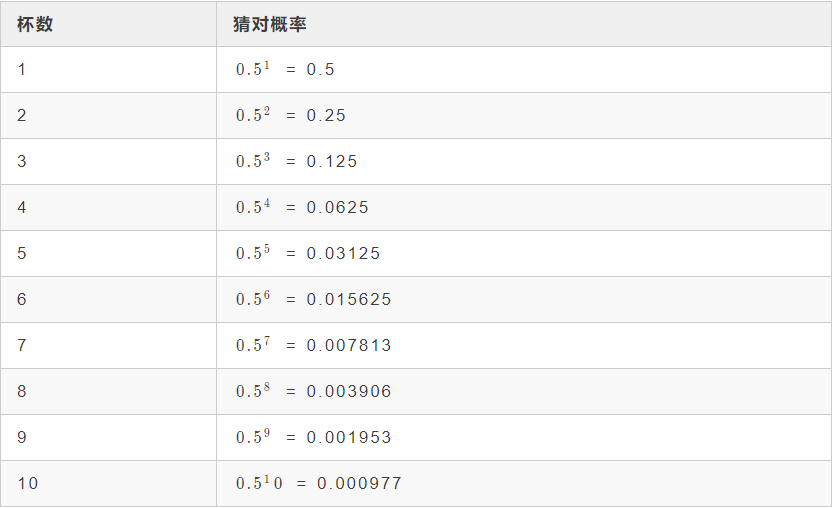
通过上表我们可以看出，连续4杯都猜对的概率不足0.1，连续10杯都猜对的概率不足0.001。如果把奶加到茶里和把茶加到奶里面得到的『奶茶』真没有差别，也就是女士要想品对，基本全靠猜，但是10杯全部猜对的概率不足0.001，我们把这种概率很小很小(这里需要定义一下，具体多小算小概率事件)的事件称为小概率事件。我们认为小概率事件一般是不会发生的，如果发生了，说明我们的认知就是错误的，也就是说女士品茶不是靠猜的，也就是把奶加到茶里和把茶加到奶里面得到的『奶茶』的确是有差别的。

我们把上面这个过程就叫做假设检验。

了解完假设检验的思想以后，我们来看一下具体步骤：

step1：提出零假设和备择假设；

零假设(H0)一般是我们要推翻的论点，备择假设(H1)则是我们要证明的论点。拿上面的女士品茶例子来讲。

H0：把茶加到奶里和把奶加到茶里面得到的『奶茶』是一样的。
H0：把茶加到奶里和把奶加到茶里面得到的『奶茶』是不一样的。

step2：构造检验统计量，并找出在H0假设成立的前提下，该统计量所服从的分布；

检验统计量是根据样本观测结果计算得到的样本统计量，并以此对零假设和备择假设做出决策。

图片来源于网络

上面图片中是三种不同的统计量以及其对应的分布，分别叫做Z检验、T检验、卡方检验。

Z检验：一般用于大样本（即样本容量大于30）平均值差异性检验的方法。它是用标准正态分布的理论来推断差异发生的概率，从而比较两个平均数的差异是否显著。在国内也被称作u检验。
T检验：主要用于样本含量较小（例如n < 30），总体标准差σ未知的正态分布。T检验是用t分布理论来推论差异发生的概率，从而比较两个平均数的差异是否显著。
卡方检验：卡方检验是统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，如果卡方值越大，二者偏差程度越大；反之，二者偏差越小；若两个值完全相等时，卡方值就为0，表明理论值完全符合。

下面为三种检验对应的分布图：

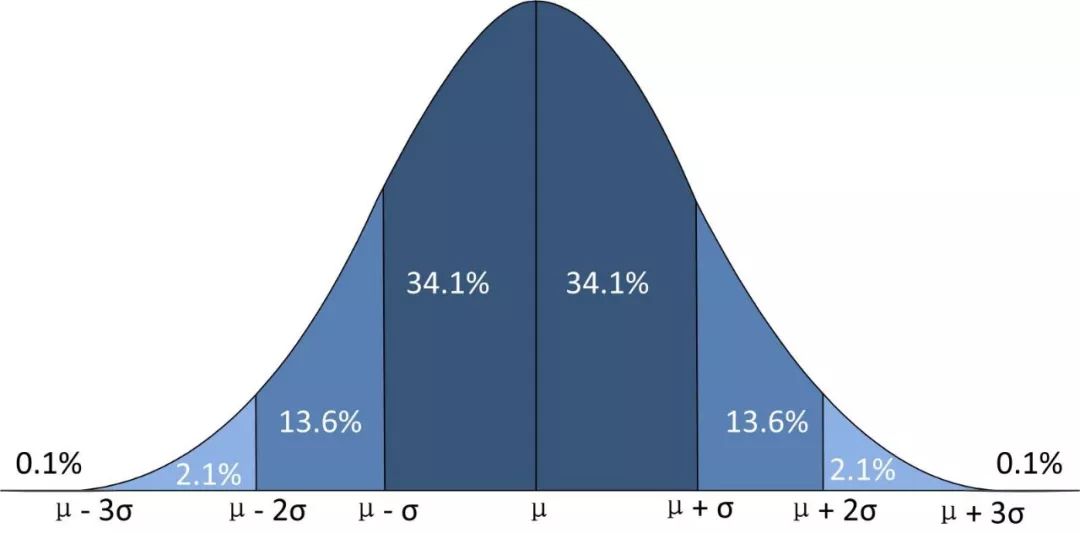
正态分布

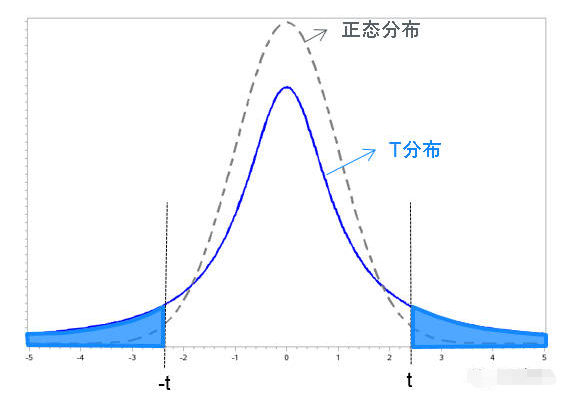
T分布，与正态类似

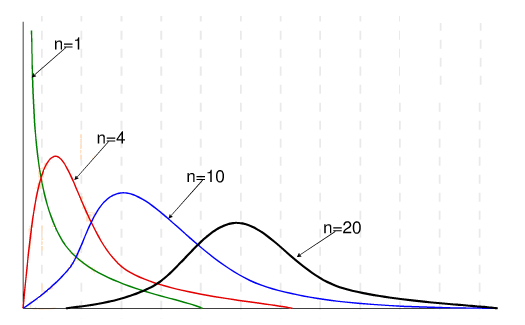
卡方分布，n为自由度

根据不同检验的特征，我们可以根据下图来进行选择合适的检验方式：

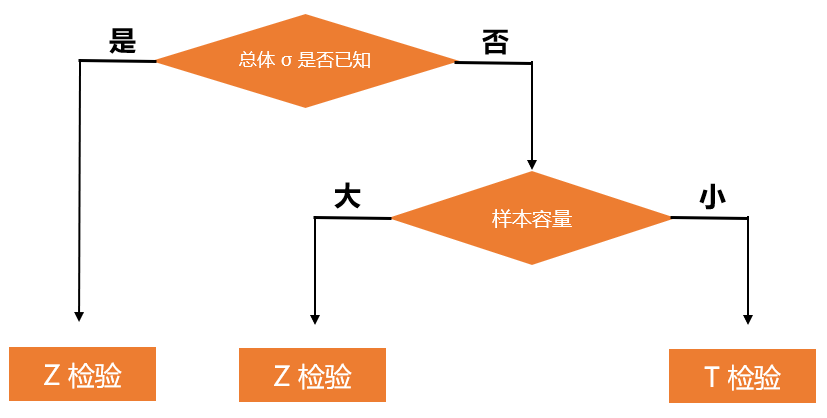
step3：根据要求的显著性水平，求临界值和拒绝域

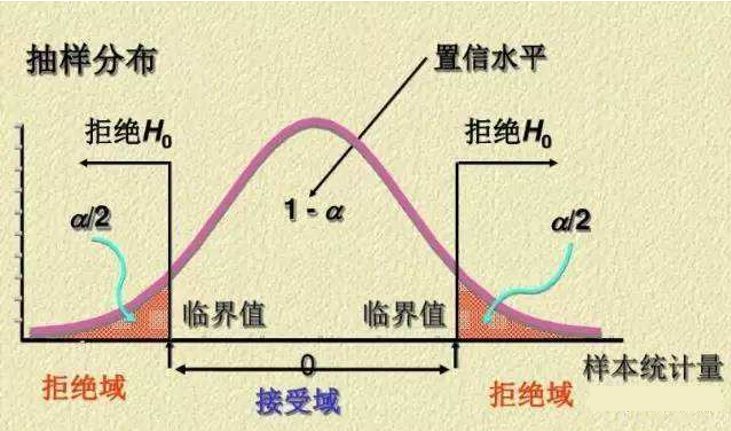
还记得我们在前面提到的小概率事件吗？如果小概率事件发生了，就表示我们的零假设是错误的，可是具体多小的概率才算是小概率呢？一般这个概率为0.05，也就是5%，如果一件事情发生的概率小于等于5%，我们就认为这是一个小概率事件，0.05就是显著性水平，用α表示。显著性水平把概率分布分为两个区间：拒绝区间和接受区间，最后计算出来的结果落在拒绝区间，我们就可以拒绝零假设；如果落在了接受区间，我们就需要接受零假设。1-α称为置信水平(置信度)。

现在我们知道了显著性水平了，然后就可以根据显著性水平求得临界值和拒绝域了。那具体怎么求呢？这里的临界值就是z值(正太分布用z值)或t值(t分布用t值)，以临界值为端点的区间称为拒绝域。z值和t值直接根据显著性水平然后到对应的z值表和t值表中查询即可。

下图为双侧检验和单侧检验对应的α、1-α、临界值、拒绝域、接受域的情况，其中α是表示阴影部分的面积，而不是x轴的值。

双侧检验

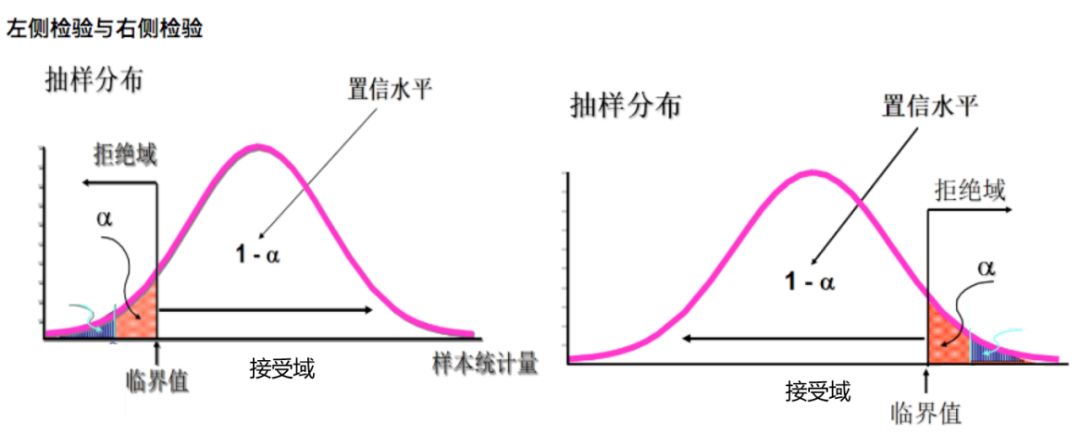
单侧检验

到这里显著性水平对应的临界值和拒绝域就算出来了。

step4：计算检验统计量

根据我们在前面选择检验统计量类型，计算对应的检验统计量的值。除此之外我们还可以根据样本量得出P值，P值就是实际样本中小概率事件的具体概率值。

step5：决策

比较计算出来的检验统计量与临界值和拒绝域，如果值落在了拒绝域内，那我们就要拒绝零假设，否则接受零假设。

比较计算出来的P值和显著性水平α值，如果P值小于等于α，则拒绝零假设，否则接受原假设。

上面两种方法分别叫做统计量检验和P值检验。

以上就是假设检验的一般流程。除此之外，假设检验里面还有两种错误，第一类错误叫做弃真错误，通俗一点就是漏诊，就是本来是生病了(假设是正确的)，但是你没有检测出来，所以给拒绝掉了；第二类错误是取伪错误，通俗一点就是误诊，就是本来没病(假设是错误的)，结果你诊断说生病了(假设是正确的)，所以就把假设给接受了。

最终判断	H0本来正确	H0本来错误
拒绝H0假设	犯I型错误	正确
接受H0假设	正确	犯II错误

I型错误的值一般为0.05，II型错误的值一般为0.1或0.2，除此之外还有一个指标叫做功效(power)，power = 1 - II型错误的值，power 表示你有多大把握能够正确的拒绝你的零假设H0。

关于假设检验我们就讲到这里，后面会分享统计学里面的其他知识，如果有想看的内容，可以评论区留言。

统计学的假设检验