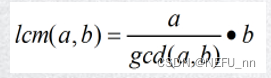gcd(m,n)=gcd(n,m%n)

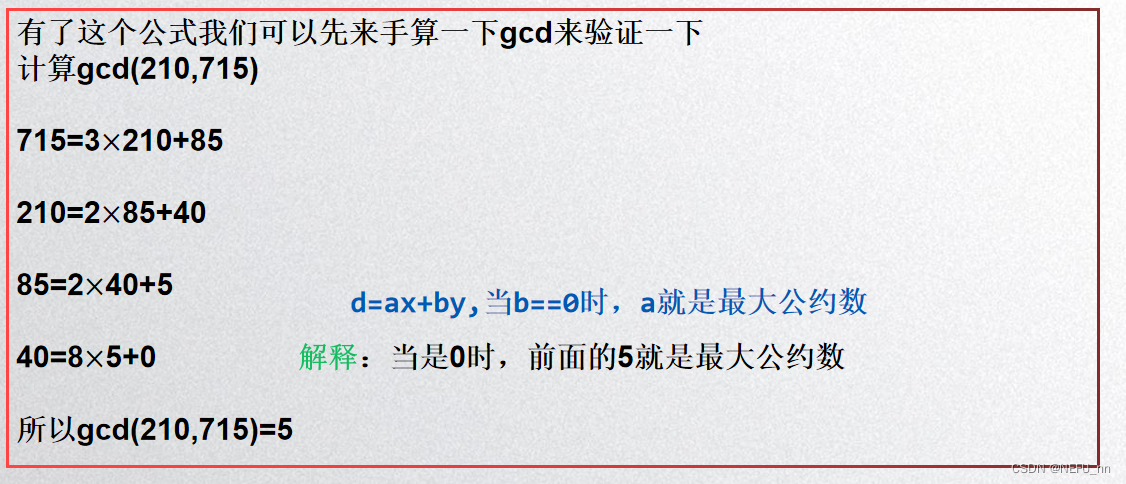
 gcd欧几里得算法标准代码求最大公约数

#include <iostream>

using namespace std;

typedef long long LL;
LL gcd(int a,int b)
{
    if(b==0)return a;
    return gcd(b,a%b);
}
int main()
{
    LL a,b;
    cin>>a>>b;
    cout<<gcd(a,b)<<endl;
    return 0;
}

LMC  最小公倍数

 这样可以防止a*b溢出

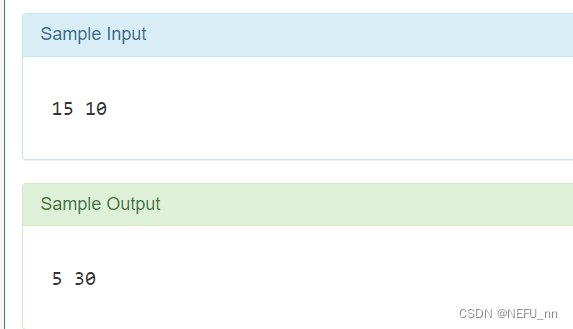
#include <iostream>
#include <stdio.h>
using namespace std;
typedef long long LL;
LL gcd(LL a, LL b)
{
    if(b==0)return a;
    return gcd(b,a%b);
}
int main()
{
    LL a,b,lmc;
    while(cin>>a>>b)
    {
    cout<<gcd(a,b)<<endl;
    lmc=a/gcd(a,b)*b;
    cout<<lmc<<endl;
    }
    return 0;
}

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int main()
{
    LL a,b,lmc,t;
    while(cin>>a>>b)
    {
        t=__gcd(a,b);
    cout<<t<<endl;
    lmc=a/t*b;
    cout<<lmc<<endl;
    }
    return 0;
}

上面这个使用了c++给我们提供的函数，要求x,y类型一致

在有些题目中我们要求求出很多个数的最大公约数和最小公倍数。 对于这种问题，基本思想就是两两合并。例如求n个数的最大公约数，就可以这样：

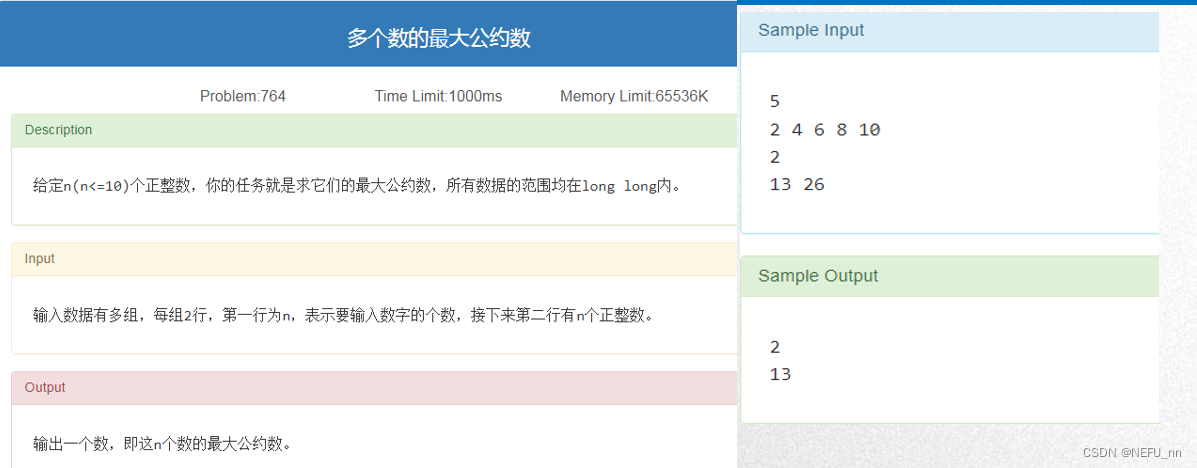
扩展欧几里得算法到底在干什么?

 扩展欧几里得算法用来解决这样一个问题：给定两个非零的整数a和b，求一组整数解（x，y），使得ax+by=gcd(a,b)成立，其中gcd(a,b)表示a和b的最大公约数。

  利用欧几里得算法的过程来计算x和y。已知递归边界成立时x=1，y=0 ，想办法反推出最开始的x和y。

x1=y2                     //x=y(old)

y1=x2-(a/b)y2        //y=x(old)-a/b*y(old);

扩展欧几里得算法背下来

void Ex_gcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return;
    }
    Ex_gcd(int b,int a%b,int x,int y)
    {
        int t;
        t=x;
        x=y;
        y=t-(a/b)*y;
    }
}

一、逆元的定义    

当 ax≡1(mod b)， x即为 a 在mod b 意义下的逆元。

    逆元的数学符号是 inv ，a 在mod b 意义下的逆元记作 inv(a,b)。注意不要写反了。        

例如5x≡1（mod 3），当x=2时满足10 ≡ 1（mod3），所以称2是5在mod 3意义下的逆元。

  (a * b) % p = (a%p * b%p) %p （对）

 (a / b) % p = (a%p / b%p) %p （错）

  在求余的过程中我们发现只有除法是不能分开运算的，而当a过大时，在计算除法过程中可能会造成比较大的精度损失，所以对于这种情况我们一般会把式子转换成那么(a / b) % p = (a * inv(b) ) % p = (a % p * inv(b) % p) % p来进行计算。这样就解决了除法不能分开计算的问题。需要注意：只有a和p互质，a才有关于p的逆元

#include <iostream>

using namespace std;

void Ex_gcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return;
    }
    Ex_gcd(b,a%b,x,y);
    {
        int t;
        t=x;
        x=y;
        y=t-(a/b)*y;
    }
}
int main()
{
    int a=5,b=7,x,y;
    Ex_gcd(a,b,x,y);
    cout<<x<<endl;
    return 0;
}