规则网络构建

文章目录

• 规则网络构建
• • @[toc]
  • • 1 规则网络定义
    • 2 规则网络的构建
    • 3 代码实现

1 规则网络定义

常见规则网络包包括全局耦合网络、最近邻耦合网络和星型耦合网络，三种规则网络定义如下：

(1)全局耦合网络：任意两个节点均存在连边的网络。

(2)最近邻耦合网络：任意节点均只与周围邻居节点相连的网络。

(3)星型耦合网络：两两不相连的$N-1$个节点均与第$N$个节点相连。

下面对最近邻耦合网络重点阐述。对于包含$N$个节点的网络，如果任意节点仅与与它最近距离(例如距离在$k=2$以内)的节点相连，则该网络称为$k$阶最近邻耦合网络。使用igraph包可以快速得到我们想要的网络。例如构造一个包含7个节点，最近邻为2的规则网络

library(igraph)
g =connect.neighborhood(graph.ring(7), 2)
plot(g)

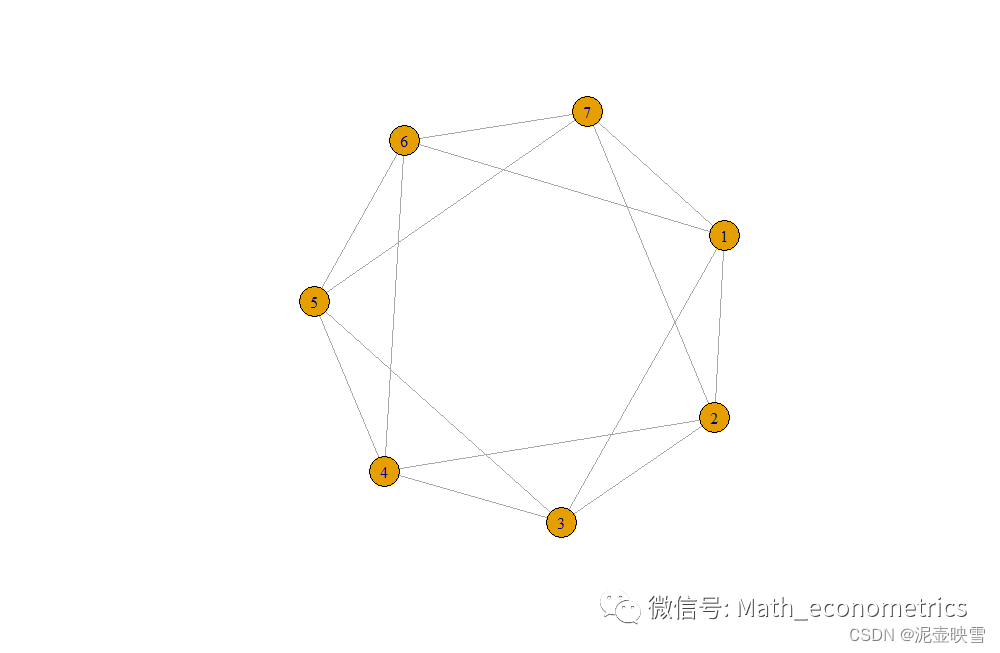
调用connect.neighborhood函数能快速构建出来。其中graph.ring(7)表示先构建包含7个节点的ring图，再选择以2为最近邻。

---

2 规则网络的构建

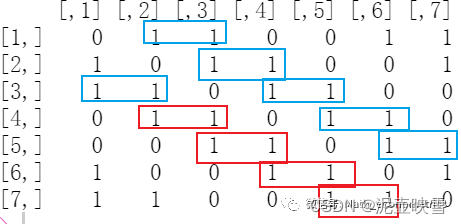
本着造轮子的想法，我们开始研究下如何自己编写最近邻耦合网络的流程。由于任何一个网络都与邻接矩阵一一对应，因此考虑从邻接矩阵入手，先分析下这种网络的元素分布规律。将上面的网络的邻接矩阵提取出来：

get.adjacency(g,sparse = FALSE)

不难看出，对于任意节点，二阶最近邻耦合网络节点对应的行，其左右两边均为1，左右两边为1的个数即为最近邻的阶数$k$。由此，下面尝试编写$k$阶最近邻耦合网络函数。

---

3 代码实现

首先明确函数输入参数，包括节点个数$N$和最近邻参数$k$。根据以上规律分析，生成最近零耦合网络算法如下：

1. 初始化节点个数和最近邻参数，初始化$N$阶零方阵。
2. 从每一行的对角线元素开始，左边和右边$k$个元素取值为1
3. 直至每一行均作用一遍。

Rule_network <- function(N,k){
  # N:节点数量
  # k最近邻居节点数
  M <- matrix(0,ncol = N,nrow = N)
  for(i in 1:N){
    for(j in 1:k){
      if(i+j<=N){
        M[i,i+j] <-  1
      }else{
        M[i,i+j-N] <- 1
      }
      if(i-j>0){
        M[i,i-j] <- 1
      }else{
        M[i,N+i-j] <- 1
      }
    }
  }
  graph <- graph_from_adjacency_matrix(M,mode = "undirected")
}

根据以上编写的Rule_network函数，生成一个20个节点，最近邻为4的规则网络

res = Rule_network(N = 20,k = 4)
plot(res,layput = layout.circle,vertex.size = 10)

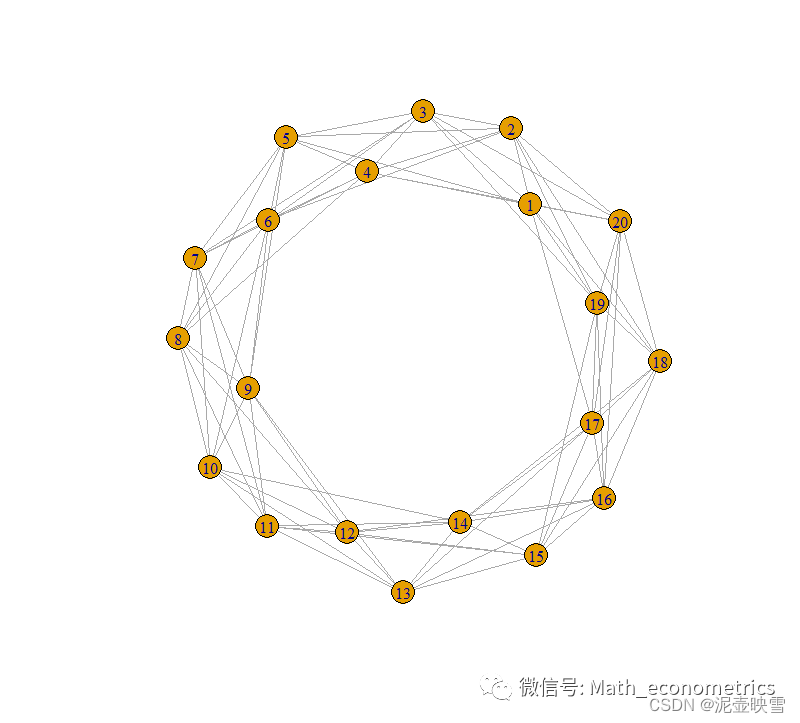
对应的邻接矩阵为

---

如果最近邻参数$k$超过大于$(N-1)/2$时，此时最近邻耦合网络即为全局耦合网络。在上述例子中，令$k=10>19/2$，

res = Rule_network(N = 20,k = 10)
plot(res,layput = layout.circle,vertex.size = 10)

对应的邻接矩阵为

---

-END-