前言：前面我们简单提及了二叉树的相关初级知识和顺序实现二叉树的相关操作详解，并且由完全二叉树延伸到了堆的相关知识，具体详见二叉树初阶和堆的详解，今天，我们展开二叉树的相关 的链式实现操作和经常考察的二叉树的相关问题，争取一次搞定二叉树的基础问题。

 

目录

1.二叉树的链式实现

1.1二叉树的三种遍历方式

1.2 二叉树创建的两种方式

 1.2.1 已知先序(后序）+中序遍历序列

          递归建树原理解释

          代码实现：

1.2.2 根据带空节点的任意一个遍历序列数组来建树

1.3 二叉树的部分功能的实现

1.3.1 层序遍历实现（BFS）

1.3.2 求二叉树的节点个数，叶子个数和高度

1.3.3 求二叉树第k层节点的个数

1.3.4 查找二叉树中数值域等于x的节点并返回

1.3.5 判断是否完全二叉树

1.4 完整代码

2.金句频道

---

1.二叉树的链式实现

      二叉树常见的创建方式可以分为两种，一种是直接通过带空节点的先序中序后序遍历中的任何一个序列创建出来，另一种则是较为常用的不带空节点的，这种就需要先序+中序或者后序+中序的组合才能确定和创建这棵二叉树,上面两种方式都与二叉树的三种遍历（先、中、后序）遍历有关，为此我们要先来了解什么是先序中序和后序遍历。

1.1二叉树的三种遍历方式

1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

比如，我这里有这样一棵二叉树：

三种遍历方式，都是从根节点出发的，只是访问和输出的规则以及顺序不一致：

       对于先序遍历来说，从根节点A出发，我们每走到一棵子树，都会先将它的根节点输出，然后再分别递归其左右子树，然后再做相同的操作，直到递归结束，得到的输出序列就是先序遍历序列。

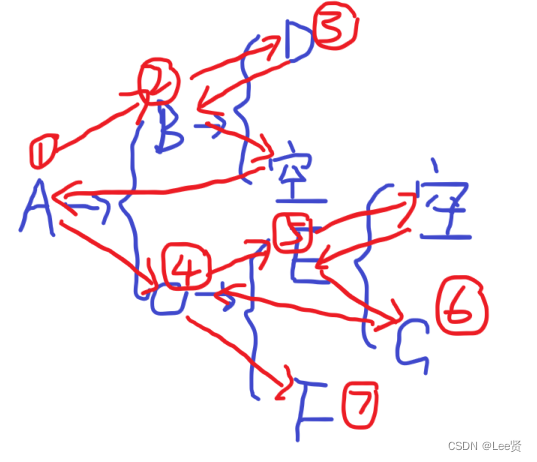
        对于中序遍历来说，还是从根节点开始遍历，但是根节点是在每一棵树的左子树“彻底”遍历完之后再输出，然后再是右子树的输出。

 对于后序遍历亦是同理，只是根在左右子树都遍历完之后输出.

       为了更好的帮助理解，我们现在直接给出三种遍历的函数实现，并在接下来采用递归调用函数栈帧的方式来帮助我们更好的理解，因为三种遍历过程思路上是一致的，一通百通，所以这里我们只是以中序遍历为例。(关于函数栈帧的相关知识，可以移步函数栈帧的创建与销毁）

//先序遍历
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		//printf("NULL ");
		return;
	}

	printf("%c ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}
//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		//printf("NULL ");
		return;
	}

	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}
//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		//printf("NULL ");
		return;
	}

	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}

我们还是选取上面的给出的样例，如下的二叉树：

 

1.2 二叉树创建的两种方式

 1.2.1 已知先序(后序）+中序遍历序列

递归建树原理解释

 代码实现：

//以样例为例的先中后序数组
Elemtype pre[] = { 'A','B','D','C','E','G','F' };//Elemtype看做char类型就好
Elemtype in[] = { 'D','B','A','E','G','C','F' };
Elemtype pos[] = { 'D','B','G','E','F','C','A'};

//根据先序和中序序列确定一棵唯一的树
void CreatTreewithpreandin(BTNode*& root, int prel, int prer,int inl, int inr)
{
	int rootidx = -1;
	if (prel <= prer && inl <= inr)
	{

		//开始寻找该子树的根节点在中序序列中的位置
		for (int i = inl; i <= inr; i++)
		{
			if (in[i] == pre[prel])//先序遍历中的对应的子树区间内的第一个节点是根节点
			{
				rootidx = i;
				break;
			}
		}
		root = BuyNode(pre[prel]);
		//求出该子树的左子树的长度
		int len = rootidx - inl;
		//递归创建左右子树
		CreatTreewithpreandin(root->left, prel + 1, prel + len, inl, rootidx - 1);
		CreatTreewithpreandin(root->right, prel + len + 1, prer, rootidx + 1, inr);
	}
	
}
//根据后序和中序序列确定一棵唯一的树
void CreatTreewithposandin(BTNode*& root,int posl, int posr, int inl, int inr)
{
	int rootidx = -1;
	if (posl <= posr && inl <= inr)
	{

		//开始寻找该子树的根节点在中序序列中的位置
		for (int i = inl; i <= inr; i++)
		{
			if (in[i] == pos[posr])//后序序列的子树区间内的最后一个节点是根节点
			{
				rootidx = i;
				break;
			}
		}
		root = BuyNode(pos[posr]);
		//求出该子树的左子树的长度
		int len = rootidx - inl;
		//递归创建左右子树
		CreatTreewithposandin(root->left, posl, posl+len-1,inl,rootidx-1);
		CreatTreewithposandin(root->right, posl + len,posr-1, rootidx + 1, inr);
	}
}

1.2.2 根据带空节点的任意一个遍历序列数组来建树

       前面说我们无法根据仅有先中后序遍历中的其中之一的数组来建树，为什么这里就可以了呢？那是因为先中后序遍历只知其一，我们无法确定二叉树的孩子结构，也就是说，一个节点到底是父节点的左孩子还是右孩子我们无法确定，因为不论是左孩子还是右孩子，在遍历中得出的结果很有可能是一致的，这也就导致了我们无法唯一的确定一棵二叉树。但是，对，但是，如果存在空节点和其他节点构成完整的子树结构，简而言之，就是假设一个树没有左孩子，那么在创建时就会将该位置补上一个特殊的符号来表示空节点，这样就可以构成完整的二叉树结构。

我们给出一个例子，比如说有一个先序数组为 "ABD##E#H##CF##G##"，其中‘#’就表示空节点，

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(Elemtype* src, int n, int* idx)//其中idx传入的是数组的当前遍历位置的下标，因为值传递会因为函数栈帧的销毁而失去效果，所以此处改为传址调用，src是前序遍历数组
{
	if (*idx >= n || src[*idx] == '#')
	{
		(*idx)++;
		return NULL;
	}

	BTNode* cur = (BTNode*)malloc(sizeof(BTNode));
	cur->data = src[*idx];
	(*idx)++;

	cur->left = BinaryTreeCreate(src, n, idx);//传地址，地址上存储的是当前遍历到的数组的下标
	cur->right = BinaryTreeCreate(src, n, idx);

	return cur;
}

1.3 二叉树的部分功能的实现

1.3.1 层序遍历实现（BFS）

       这部分我使用了C++的queue来实现，之前我们实现过的模拟队列也可以实现，只是过程稍加繁琐，层序遍历就是按二叉树的高度遍历，从根节点开始，逐层往下遍历，我们可以使用队列，在逐层访问时将根节点的左右孩子入队，当父节点层遍历完毕时，队首元素就是下一层的遍历顺序。

//层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	//迭代法利用队列进行宽度优先遍历(C++STL)
	queue<BTNode*> mp;
	if (!root)
		return;
	mp.push(root);
	while (!mp.empty())
	{
		BTNode* temp = mp.front();
		printf("%c ", temp->data);
		mp.pop();
		if (temp->left)
			mp.push(temp->left);
		if (temp->right)
			mp.push(temp->right);
	}
}    

1.3.2 求二叉树的节点个数，叶子个数和高度

 这部分就老生常谈了，但凡会递归的，这些都不是问题啦，那我就直接......，嘿嘿~~

// 二叉树结点个数
int BTreeSize(BTNode* root)
{

	return root == NULL ? 0 : BTreeSize(root->left)
		+ BTreeSize(root->right) + 1;
}

// 求叶子节点的个数
int BTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	if (root->left == NULL
		&& root->right == NULL)
	{
		return 1;
	}

	return BTreeLeafSize(root->left)
		+ BTreeLeafSize(root->right);
}

//二叉树的高度
int BTreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;

	int leftHeight = BTreeHeight(root->left);
	int rightHeight = BTreeHeight(root->right);//注意这种保存值的方式更加高效，可以画递归图证明

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

1.3.3 求二叉树第k层节点的个数

       还是递归，求解第k层的节点，假设k=3，在二叉树有第三层的条件下，我们在递归遍历的过程中，每次进入一个父节点的孩子节点遍历时，k就减1，当k到1时就到了第k层，开始计数即可。

// 二叉树第k层结点个数
int BTreeLevelKSize(BTNode* root, int k)
{
	assert(k > 0);

	if (root == NULL)
		return 0;

	if (k == 1)
		return 1;

	return BTreeLevelKSize(root->left, k - 1)
		+ BTreeLevelKSize(root->right, k - 1);
}

1.3.4 查找二叉树中数值域等于x的节点并返回

       这个函数一定要画个递归逻辑图，否则很有可能调到坑里去，如果我们在递归遍历的某个节点返回的话，并不是直接结束函数返回值，而是返回的该函数的上一层调用，所以，我们在递归调用左右子树时，需要判断返回。

//二叉树查找节点值为x的节点
BTNode* BinaryTreeFind(BTNode* root, Elemtype x)
{
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;
	BTNode* left= BinaryTreeFind(root->left, x);//遍历完左子树看left的返回值
	if (left)
		return left;
	return  BinaryTreeFind(root->right, x);//如果程序执行到了这一步，就说明有x也一定在右子树里，或者没有就可以直接返回NULL

}

1.3.5 判断是否完全二叉树

这个问题就要考虑一会了，我们先来想想完全二叉树是什么概念来着？

完全二叉树是一种特殊的二叉树结构，它具有以下两个特点：

1. 满二叉树：除了叶子节点，每个节点都有两个子节点，且所有叶子节点都在同一层级上。

2. 节点分布均匀：在最后一层的节点如果不满，则只有在最后一层的右侧可以出现缺少的节点，其余各层节点都是满的，且最后一层节点必须按照从左到右的顺序排列。

       对完全二叉树最重要的定义就是叶子节点只能出现在最下层和次下层，所以我们想到可以使用队列辅助进行层次遍历——从上到下遍历所有层，每层从左到右，只有次下层和最下层才有叶子节点，其他层出现叶子节点就意味着不是完全二叉树。

// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	if (root == NULL)
		return true;//空树一定是完全二叉树
	queue<BTNode*> mp;
	bool flag = false;
	mp.push(root);
	while (!mp.empty())
	{
		int sz = mp.size();
		for (int i = 0; i < sz; i++)
		{
			BTNode* temp = mp.front();
			mp.pop();
			if (temp->left != NULL)
			{
				mp.push(temp->left);
				if (flag)//表示已经是完全二叉树的叶子节点了(该处存在空节点，所以应该是最后了)
					return false;
			}
			else
			{
				//如果遇到了空节点，那么flag=true表示到了满足完全二叉树的最后的节点
				flag = true;
			}
			if (temp->right != NULL)
			{
				mp.push(temp->right);
				if (flag)//表示已经是完全二叉树的叶子节点了(该处存在空节点，所以应该是最后了)
					return false;
			}
			else
			{
				//如果遇到了空节点，那么flag=true表示到了满足完全二叉树的最后的节点
				flag = true;
			}

		}
	}
	return true;
}

1.4 完整代码

#include <bits/stdc++.h>
using namespace std;
typedef char Elemtype;

typedef struct node {
	Elemtype data;
	struct node* left;
	struct node* right;
}BTNode;

//先中后序数组
Elemtype pre[] = { 'A','B','D','C','E','G','F' };
Elemtype in[] = { 'D','B','A','E','G','C','F' };
Elemtype pos[] = { 'D','B','G','E','F','C','A'};
Elemtype pre2[] = { 'A','B','D','#','#','E','#','H','#','#','C','F','#','#','G','#','#' };
//创建新节点
BTNode* BuyNode(Elemtype x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}

	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;
}
//我们也可以根据带空节点的先序后序中序数组中的任意一个数组来确定一棵唯一的二叉树(这里以先序数组为例，‘N'表示此处为空)
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(Elemtype* src, int n, int* idx)
{
	if (*idx >= n || src[*idx] == '#')
	{
		(*idx)++;
		return NULL;
	}

	BTNode* cur = (BTNode*)malloc(sizeof(BTNode));
	cur->data = src[*idx];
	(*idx)++;

	cur->left = BinaryTreeCreate(src, n, idx);//传地址，地址上存储的是当前遍历到的数组的下标
	cur->right = BinaryTreeCreate(src, n, idx);

	return cur;
}

//根据先序和中序序列确定一棵唯一的树
void CreatTreewithpreandin(BTNode*& root, int prel, int prer,int inl, int inr)
{
	int rootidx = -1;
	if (prel <= prer && inl <= inr)
	{

		//开始寻找该子树的根节点在中序序列中的位置
		for (int i = inl; i <= inr; i++)
		{
			if (in[i] == pre[prel])//先序遍历中的对应的子树区间内的第一个节点是根节点
			{
				rootidx = i;
				break;
			}
		}
		root = BuyNode(pre[prel]);
		//求出该子树的左子树的长度
		int len = rootidx - inl;
		//递归创建左右子树
		CreatTreewithpreandin(root->left, prel + 1, prel + len, inl, rootidx - 1);
		CreatTreewithpreandin(root->right, prel + len + 1, prer, rootidx + 1, inr);
	}
	
}
//根据后序和中序序列确定一棵唯一的树
void CreatTreewithposandin(BTNode*& root,int posl, int posr, int inl, int inr)
{
	int rootidx = -1;
	if (posl <= posr && inl <= inr)
	{

		//开始寻找该子树的根节点在中序序列中的位置
		for (int i = inl; i <= inr; i++)
		{
			if (in[i] == pos[posr])//后序序列的子树区间内的最后一个节点是根节点
			{
				rootidx = i;
				break;
			}
		}
		root = BuyNode(pos[posr]);
		//求出该子树的左子树的长度
		int len = rootidx - inl;
		//递归创建左右子树
		CreatTreewithposandin(root->left, posl, posl+len-1,inl,rootidx-1);
		CreatTreewithposandin(root->right, posl + len,posr-1, rootidx + 1, inr);
	}
}

//先序遍历
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		//printf("NULL ");
		return;
	}

	printf("%c ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}
//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		//printf("NULL ");
		return;
	}

	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}
//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		//printf("NULL ");
		return;
	}

	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}

//层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	//迭代法利用队列进行宽度优先遍历(C++STL)
	queue<BTNode*> mp;
	if (!root)
		return;
	mp.push(root);
	while (!mp.empty())
	{
		BTNode* temp = mp.front();
		printf("%c ", temp->data);
		mp.pop();
		if (temp->left)
			mp.push(temp->left);
		if (temp->right)
			mp.push(temp->right);
	}
}    
// 二叉树结点个数
int BTreeSize(BTNode* root)
{

	return root == NULL ? 0 : BTreeSize(root->left)
		+ BTreeSize(root->right) + 1;
}

// 求叶子节点的个数
int BTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	if (root->left == NULL
		&& root->right == NULL)
	{
		return 1;
	}

	return BTreeLeafSize(root->left)
		+ BTreeLeafSize(root->right);
}

//二叉树的高度
int BTreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;

	int leftHeight = BTreeHeight(root->left);
	int rightHeight = BTreeHeight(root->right);

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

// 二叉树第k层结点个数
int BTreeLevelKSize(BTNode* root, int k)
{
	assert(k > 0);

	if (root == NULL)
		return 0;

	if (k == 1)
		return 1;

	return BTreeLevelKSize(root->left, k - 1)
		+ BTreeLevelKSize(root->right, k - 1);
}

// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	if (root == NULL)
		return true;//空树一定是完全二叉树
	queue<BTNode*> mp;
	bool flag = false;
	mp.push(root);
	while (!mp.empty())
	{
		int sz = mp.size();
		for (int i = 0; i < sz; i++)
		{
			BTNode* temp = mp.front();
			mp.pop();
			if (temp->left != NULL)
			{
				mp.push(temp->left);
				if (flag)//表示已经是完全二叉树的叶子节点了(该处存在空节点，所以应该是最后了)
					return false;
			}
			else
			{
				//如果遇到了空节点，那么flag=true表示到了满足完全二叉树的最后的节点
				flag = true;
			}
			if (temp->right != NULL)
			{
				mp.push(temp->right);
				if (flag)//表示已经是完全二叉树的叶子节点了(该处存在空节点，所以应该是最后了)
					return false;
			}
			else
			{
				//如果遇到了空节点，那么flag=true表示到了满足完全二叉树的最后的节点
				flag = true;
			}

		}
	}
	return true;
}

//二叉树查找节点值为x的节点
BTNode* BinaryTreeFind(BTNode* root, Elemtype x)
{
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;
	BTNode* left= BinaryTreeFind(root->left, x);//遍历完左子树看left的返回值
	if (left)
		return left;
	return  BinaryTreeFind(root->right, x);//如果程序执行到了这一步，就说明有x也一定在右子树里，或者没有就可以直接返回NULL

}
//二叉树的销毁
void BinaryTreeDestory(BTNode*& root)//引用可以用二级指针代替
{
	if (root)
	{
		BinaryTreeDestory(root->left);
		BinaryTreeDestory(root->right);
		free(root);
		root = NULL;
	}
}
int main()
{
	BTNode* root=NULL;
	//根据先序和中序建树
	/*CreatTreewithpreandin(root, 0, 6, 0, 6);
	printf("后序遍历序列为：->\n");
	PostOrder(root);*/

	//根据后序和中序建树
	/*CreatTreewithposandin(root, 0, 6, 0, 6);
	printf("先序遍历序列为：->\n");
	PrevOrder(root);*/

	//根据带空节点的先序序列建树
	int idx = 0;
	root=BinaryTreeCreate(pre2,17,&idx);
	printf("先序遍历序列为：->\n");
	PrevOrder(root);
	printf("\n层序遍历序列为：->\n");
	BinaryTreeLevelOrder(root);
	
	return 0;
}

2.金句频道

       你就应该满脑子都是前途，不用在意别人的看法，不再害怕别人讨厌自己，不在畏手畏脚忧心忡忡，也不会在睡前反复回忆白天的行为，是否会让对方产生误解。要么努力往上爬，要么永远烂在底层里，这就是现实，没有可以依靠的人，那就自己拼命地努力。