代码随想录刷题Day53 | 1143. 最长公共子序列 | 1035. 不相交的线 | 53. 最大子数组和

1143. 最长公共子序列

题目：

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

• 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。

思路：

1. 确定dp数组（dp table）以及下标的含义

dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]

有同学会问：为什么要定义长度为[0, i - 1]的字符串text1，定义为长度为[0, i]的字符串text1不香么？

这样定义是为了后面代码实现方便，如果非要定义为为长度为[0, i]的字符串text1也可以，大家可以试一试！

2. 确定递推公式

主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同

如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;

如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。

即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

代码如下：

if (text1[i - 1] == text2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}

3. dp数组如何初始化

先看看dp[i][0]应该是多少呢？

test1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0;

同理dp[0][j]也是0。

其他下标都是随着递推公式逐步覆盖，初始为多少都可以，那么就统一初始为0。

代码：

vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));

4. 确定遍历顺序

从递推公式，可以看出，有三个方向可以推出dp[i][j]，如图：

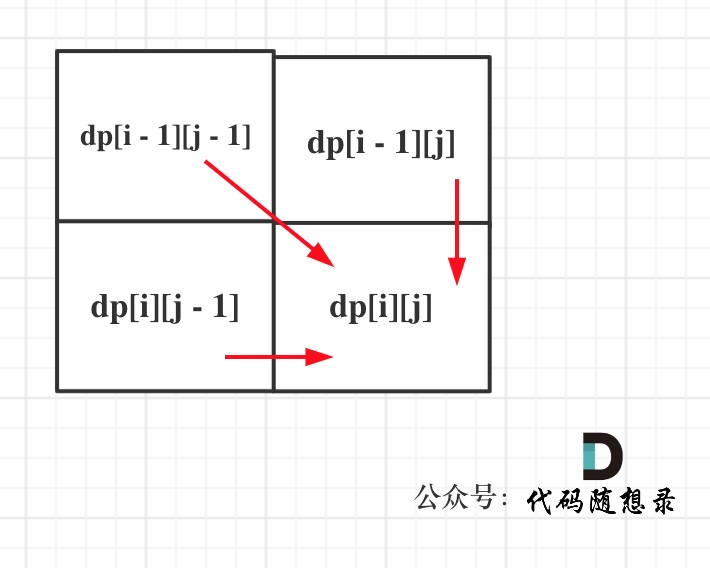
那么为了在递推的过程中，这三个方向都是经过计算的数值，所以要从前向后，从上到下来遍历这个矩阵。

5. 举例推导dp数组

以输入：text1 = “abcde”, text2 = “ace” 为例，dp状态如图：

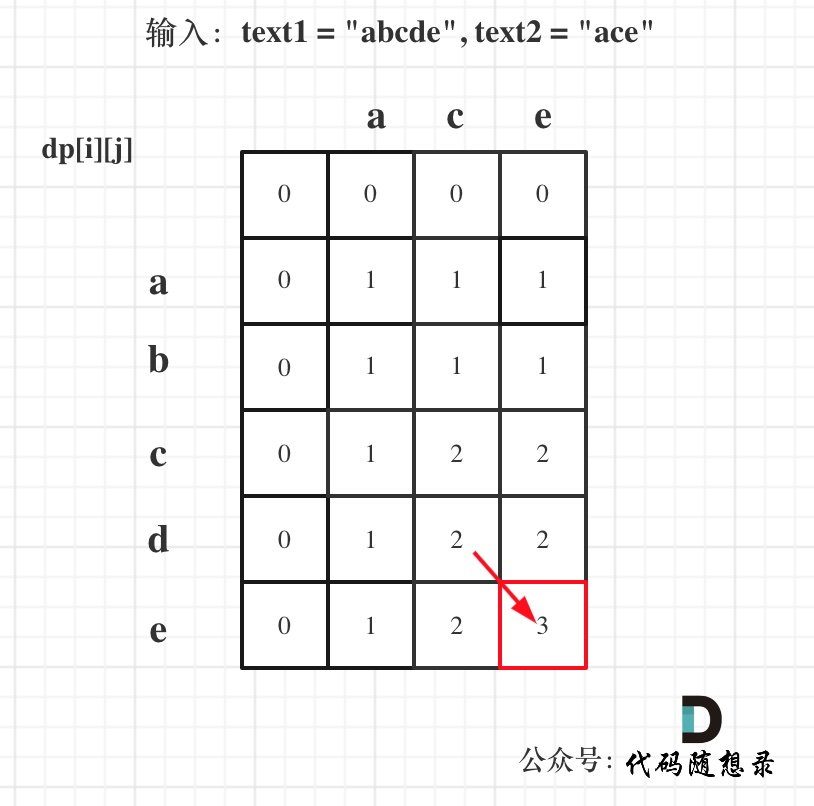
最后红框dp[text1.size()][text2.size()]为最终结果

代码：

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int[][] dp = new int[text1.length() + 1][text2.length() + 1];
        for(int i = 1; i <= text1.length(); i++){
            for(int j = 1; j <= text2.length(); j++){
                if(text1.charAt(i - 1) == text2.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else{
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[text1.length()][text2.length()];
    }
}

1035. 不相交的线

题目：

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

• nums1[i] == nums2[j]
• 且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

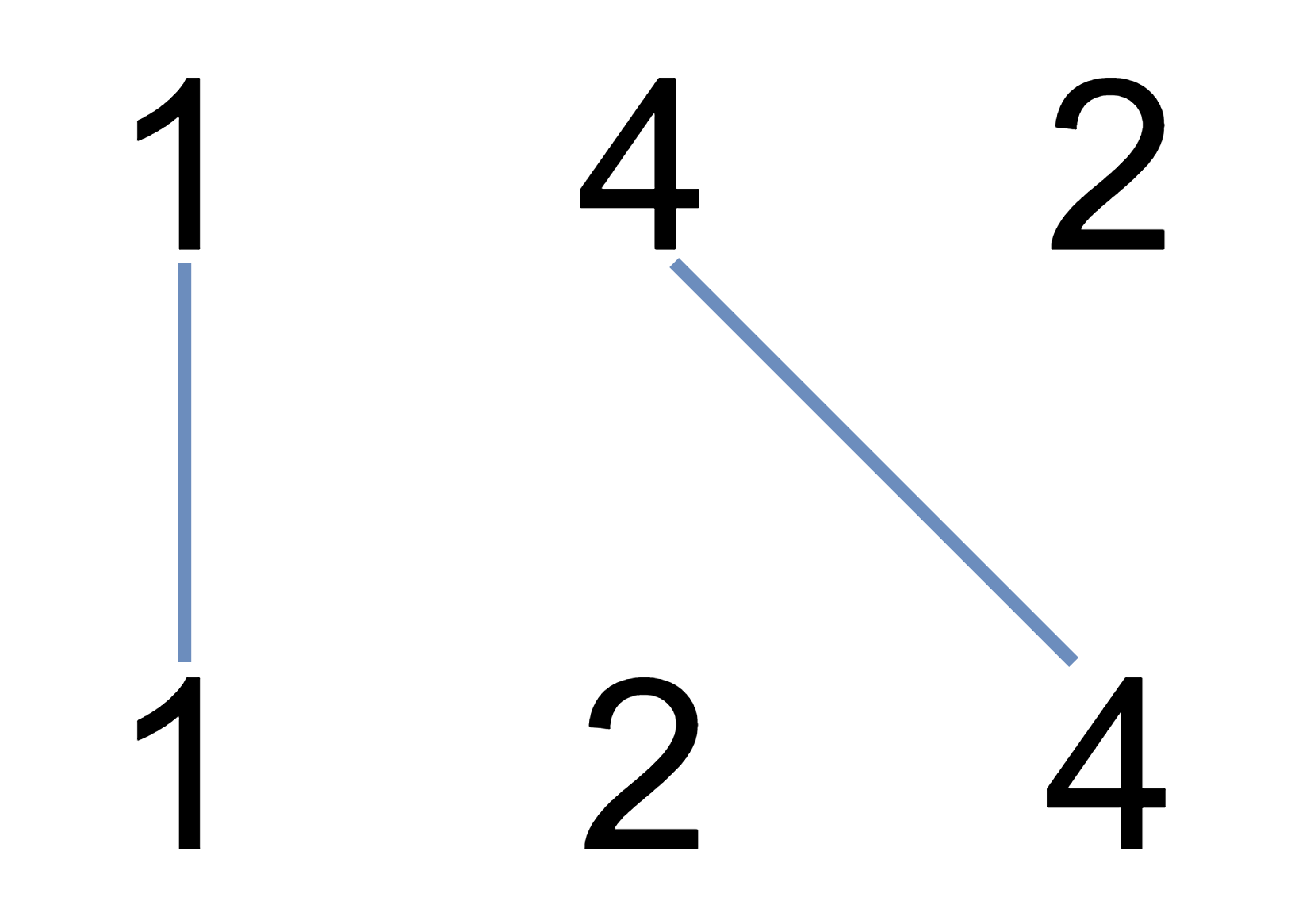
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

思路：

绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且直线不能相交！

直线不能相交，这就是说明在字符串A中 找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。

拿示例一A = [1,4,2], B = [1,2,4]为例，相交情况如图：

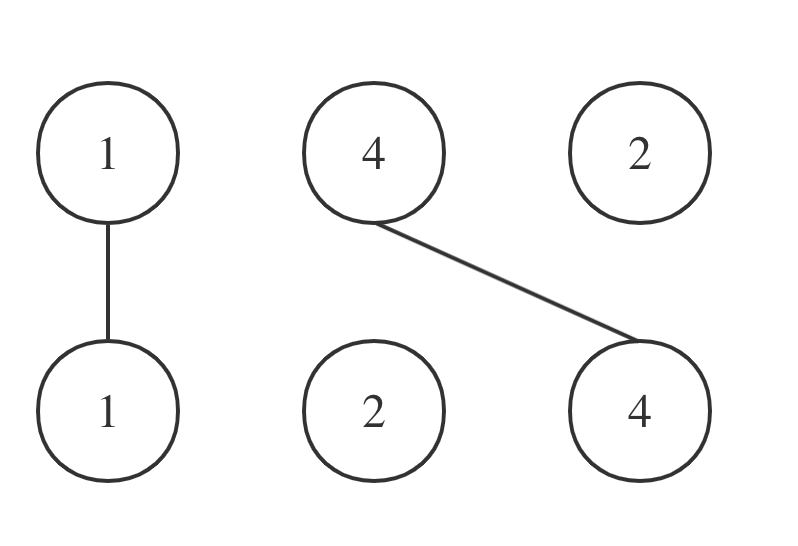
其实也就是说A和B的最长公共子序列是[1,4]，长度为2。 这个公共子序列指的是相对顺序不变（即数字4在字符串A中数字1的后面，那么数字4也应该在字符串B数字1的后面）

这么分析完之后，大家可以发现：本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！

代码：

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int[][] dp = new int[nums1.length + 1][nums2.length + 1];
        for(int i = 1; i <= nums1.length; i++){
            for(int j = 1; j <= nums2.length; j++){
                if(nums1[i - 1] == nums2[j - 1]){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else{
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[nums1.length][nums2.length];
    }
}

53. 最大子数组和

题目：

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

思路：

动规五部曲如下：

1. 确定dp数组（dp table）以及下标的含义

dp[i]：包括下标i之前的最大连续子序列和为dp[i]。

2. 确定递推公式

dp[i]只有两个方向可以推出来：

• dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
• nums[i]，即：从头开始计算当前连续子序列和

一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);

3. dp数组如何初始化

从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态，dp[0]就是递推公式的基础。

dp[0]应该是多少呢?

根据dp[i]的定义，很明显dp[0]应为nums[0]即dp[0] = nums[0]。

4. 确定遍历顺序

递推公式中dp[i]依赖于dp[i - 1]的状态，需要从前向后遍历。

5. 举例推导dp数组

以示例一为例，输入：nums = [-2,1,-3,4,-1,2,1,-5,4]，对应的dp状态如下：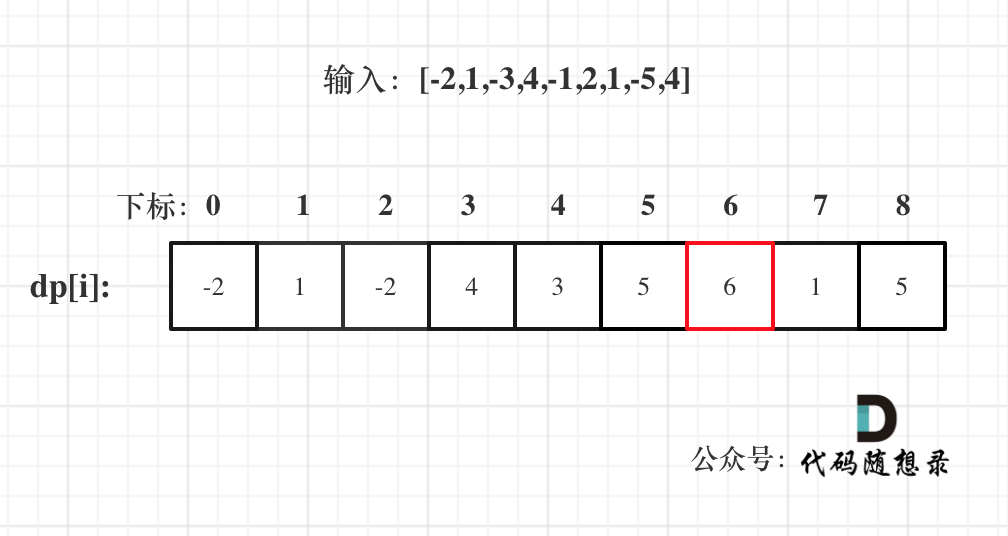

代码：

class Solution {
    public int maxSubArray(int[] nums) {
        int[] dp = new int[nums.length];
        dp[0] = nums[0] > 0 ? nums[0] : 0;
        int res = nums[0];
        for(int i = 1; i < nums.length; i++){
            dp[i] =Math.max(dp[i - 1] + nums[i], nums[i]);
            if(dp[i] > res){
                res = dp[i];
            }
        }
        return res;
    }
}