总体与个体

总体：试验的全部可能的观察值称为总体
个体：总体中每个可能的观察值称为个体

总体期望=样本平均期望
总体方差/n=样本平均方差

随机样本

X₁，X₂……X_n相互独立（x₁，x₂……x_n是观察值），称为总体X的一个简单随机变量（样本）

联合=（全部）边缘相乘

统计量

函数表示化（不含未知参数，不一定是线性关系函数）

常用统计量

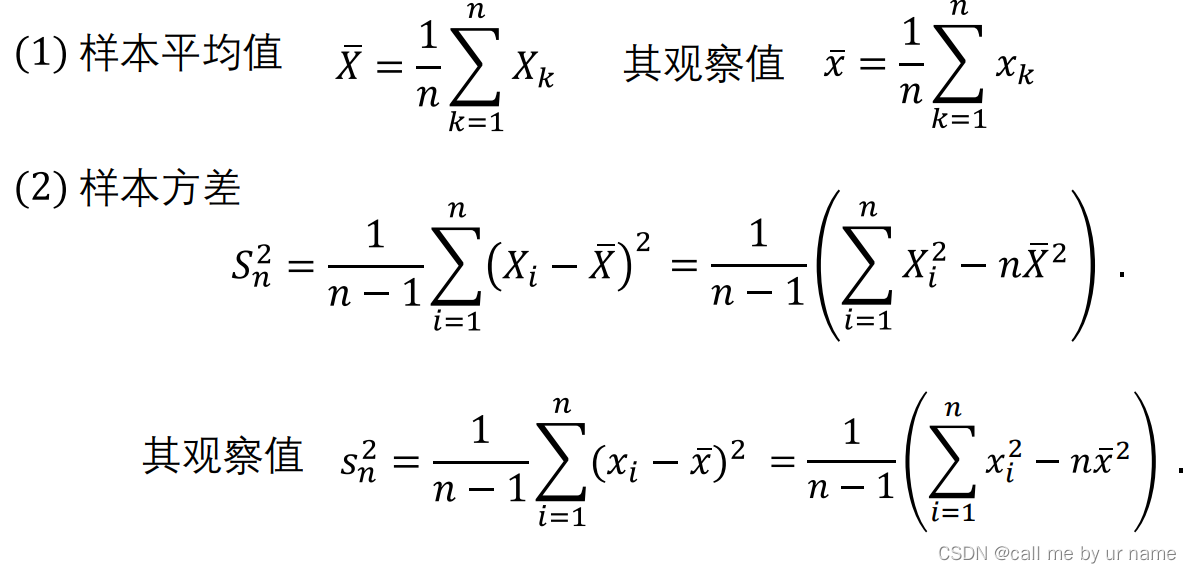
主要是要知道S_n²是样本方差的意思并且，系数为1/n-1

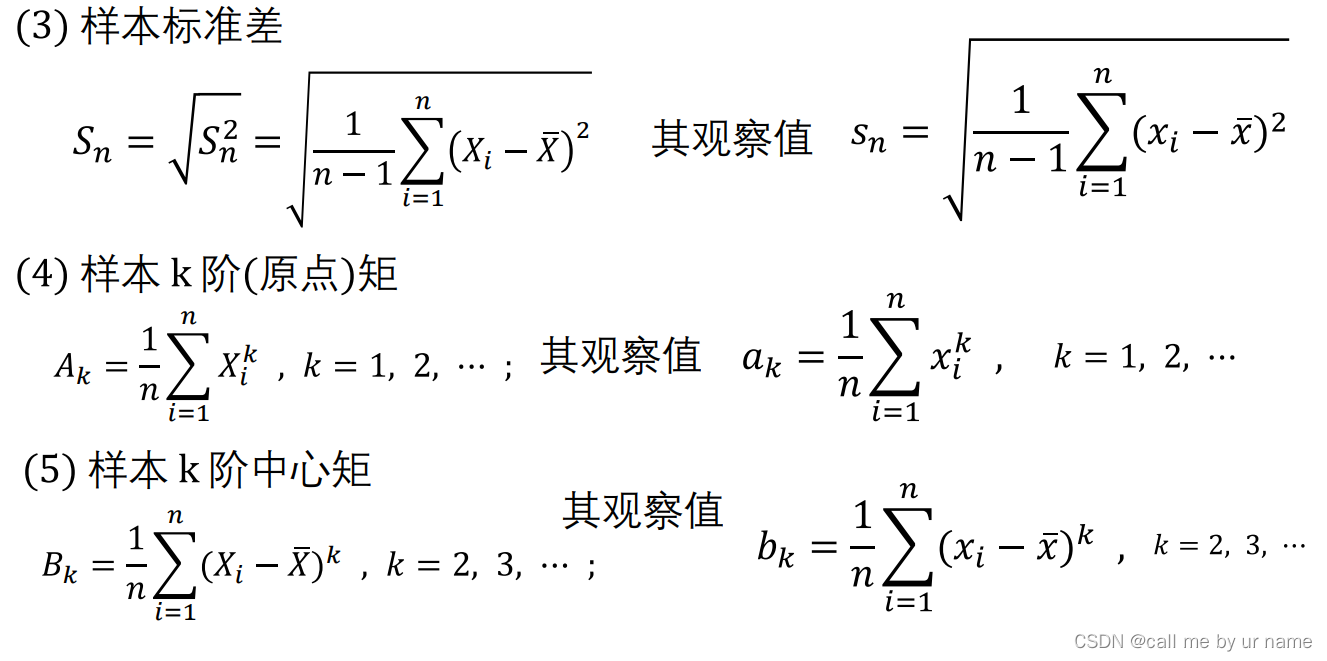
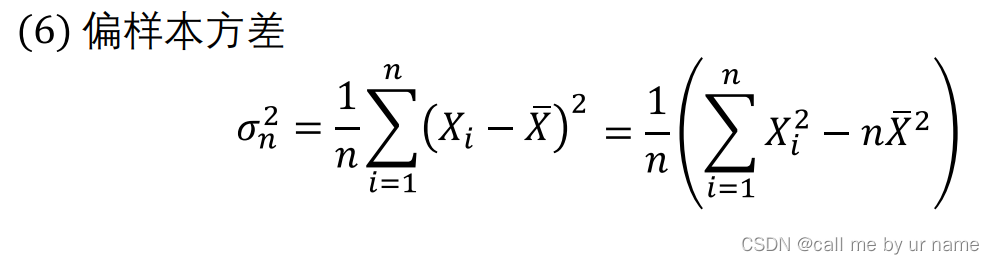
首先知道各个符号代表什么意思要乘以1/n，因为是样本的值：
A——原点矩
B——中心矩
σ_n——偏样本方差下标带了个n，相当于2阶中心矩，后面的那个公式尽量记住

样本矩的性质

理解：
总体的期望=样本平均的期望
样本平均的方差=总体方差/n
样本方差的期望=总体方差（这个很好理解了，大量样本就跟总体一样）
样本偏差的期望——用样本方差的期望可以推出来

常见分布

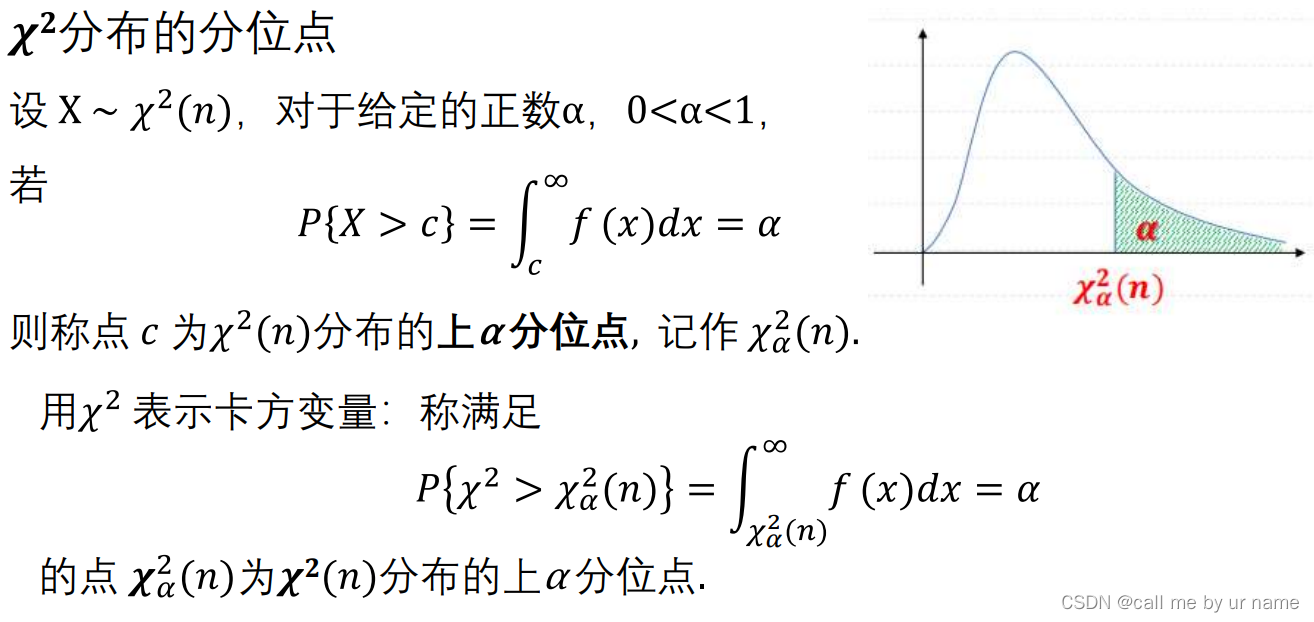
χ²分布（卡方分布）

概率密度函数不用掌握
卡方分布由相互独立的正态分布组成

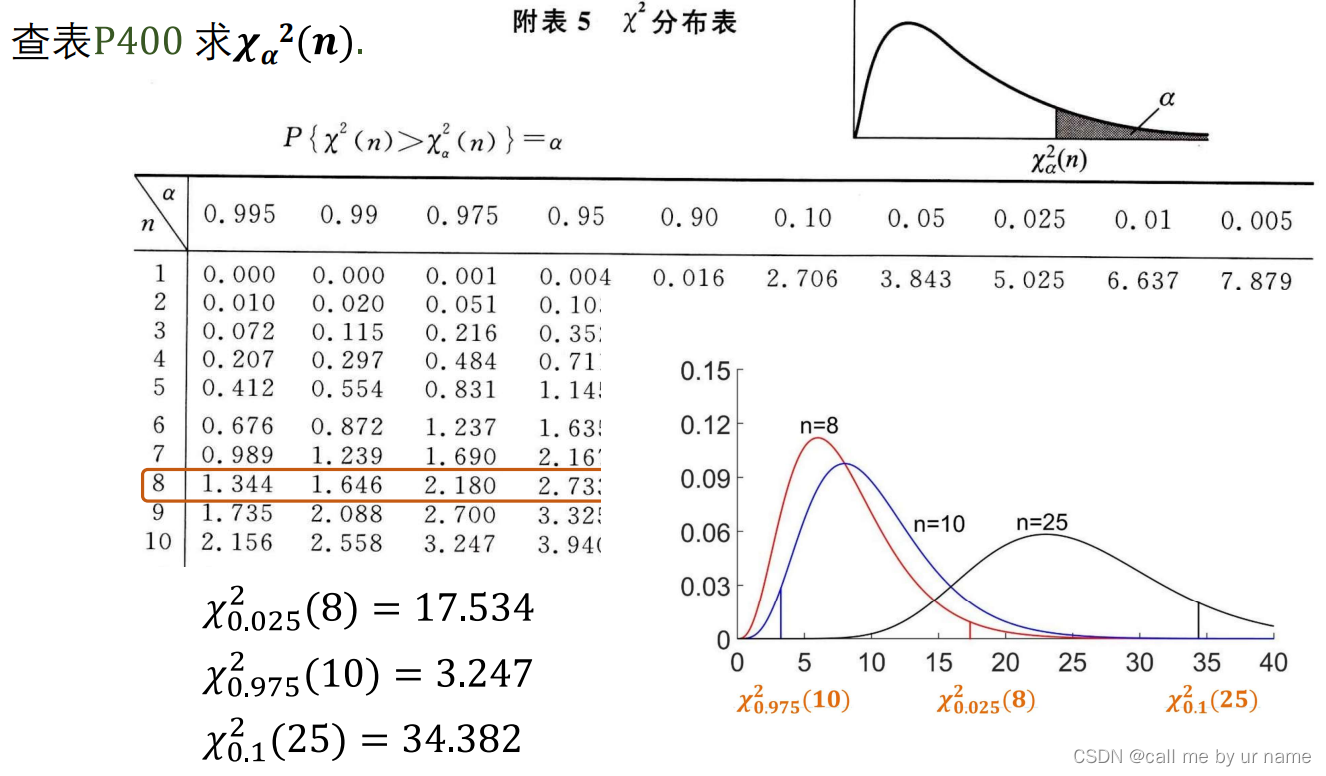
χ²分布的上α分位点

性质

要求X₁和X₂相互独立

例

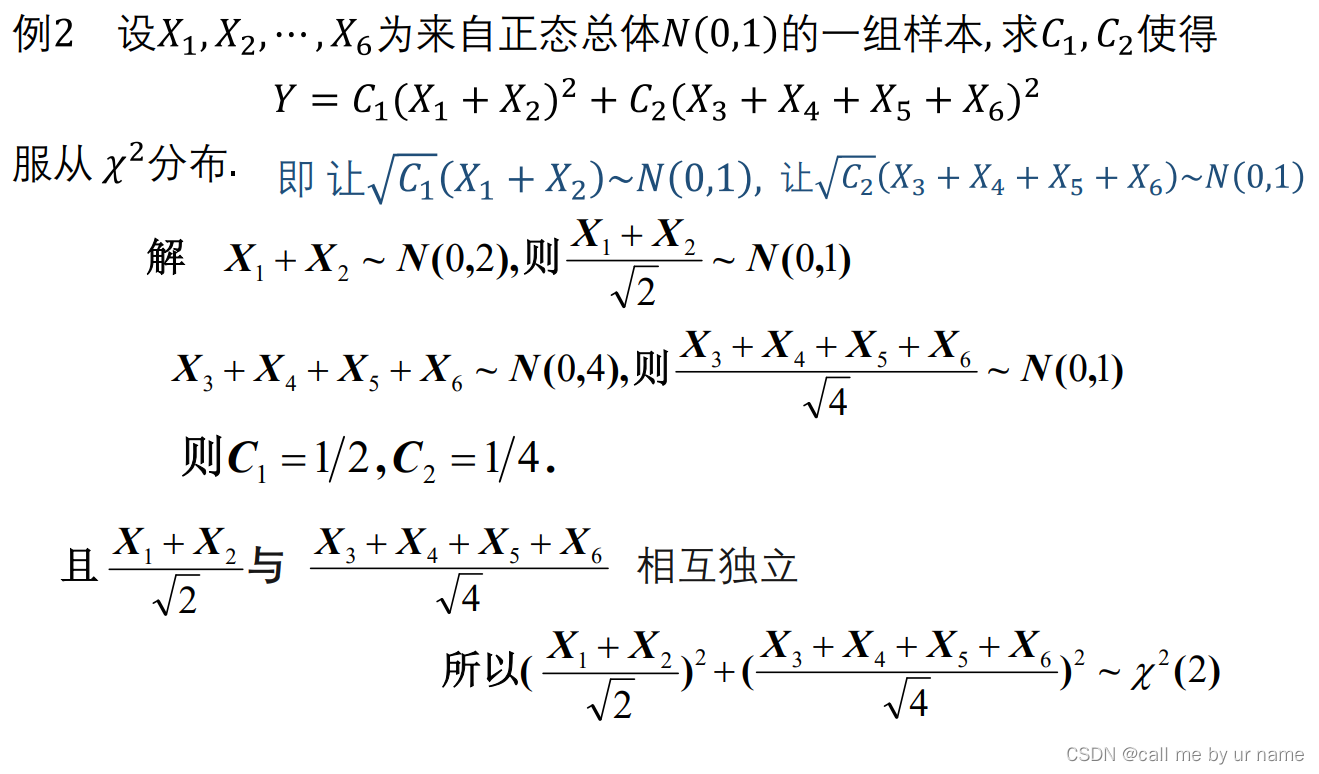
样本之间相互独立
服从卡方分布，需要变量的平方的和，所以取C₁块和C₂块的根号，服从正态分布（因为正态分布相互独立情况下具有可加性）

次序统计量

简而言之——从小到大排（X_（1）是min函数，X_(n)是max函数）

经验分布函数

F_n(x)——经验分布函数

性质

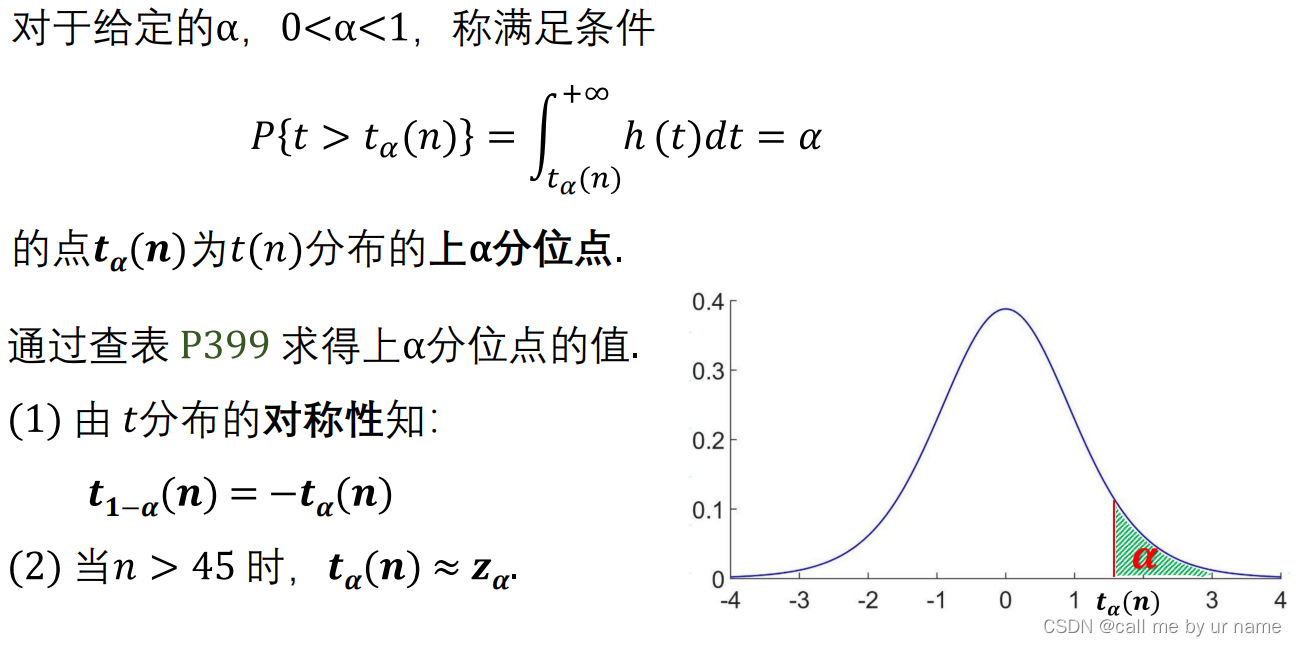
t分布

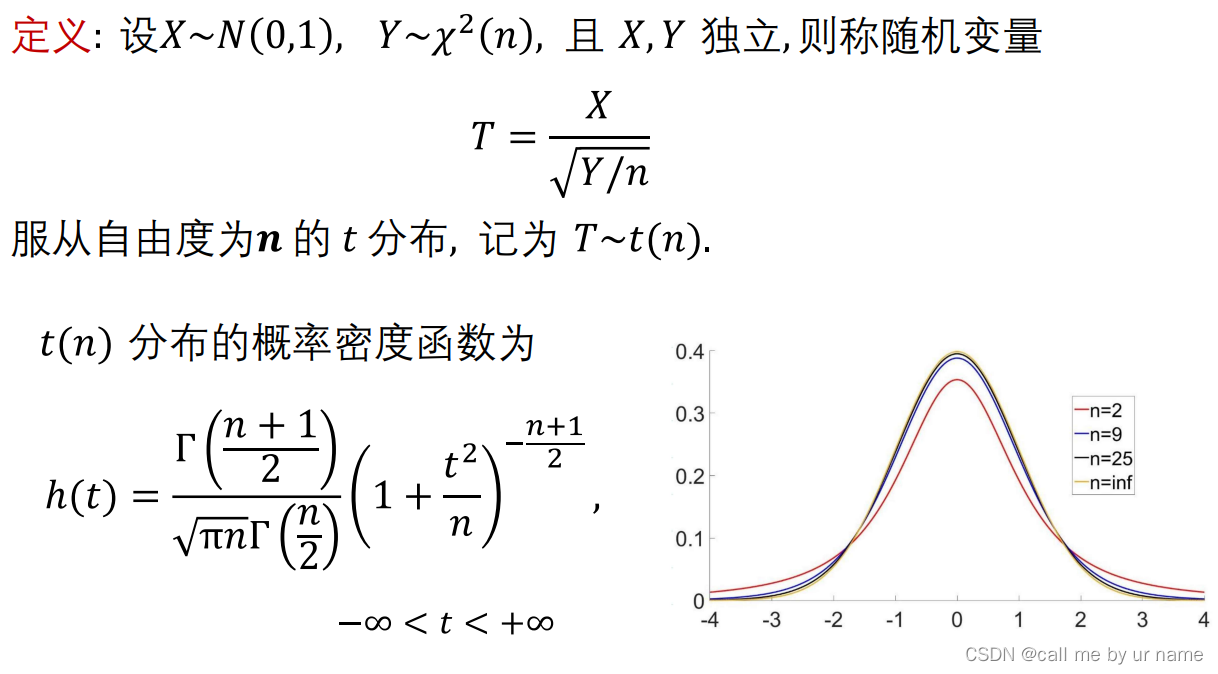
分母要带根号分母带根号，那么就是t分布
X,Y要独立分布
X~N(0,1)， Y~χ²，分母是根号下卡方分布/自由度
概率密度函数不需要掌握

性质

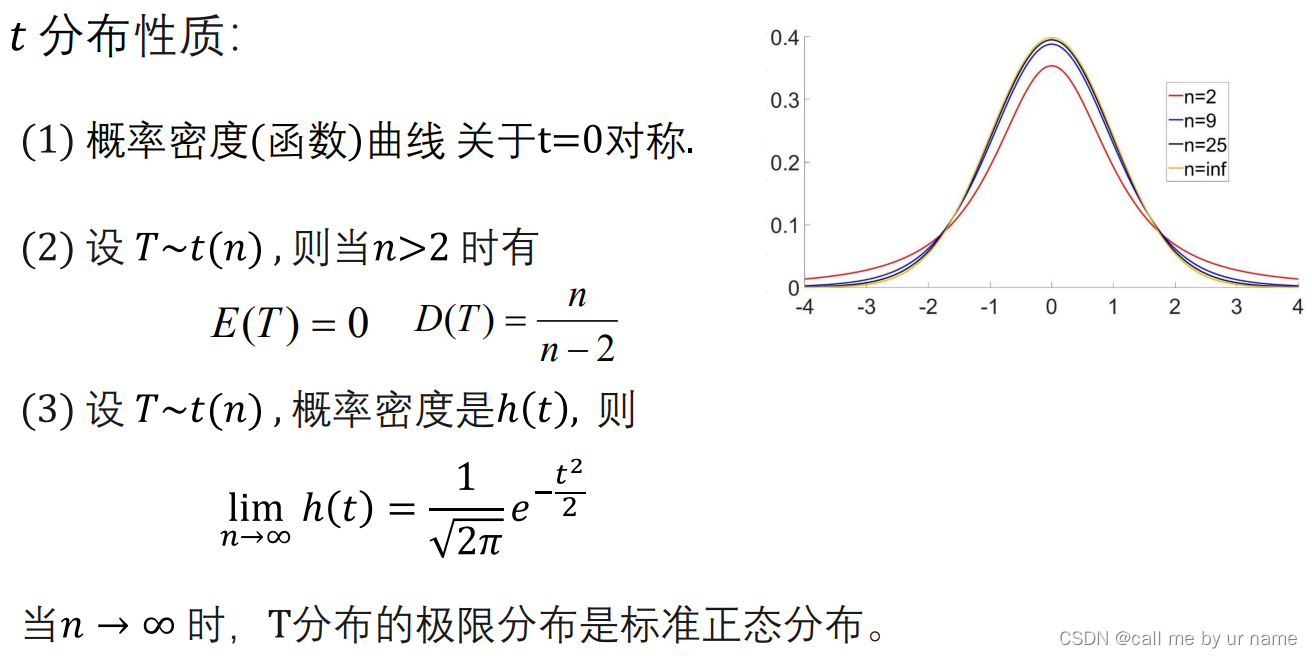
T表示服从t(n)的函数

t分布的上α分位点

F分布

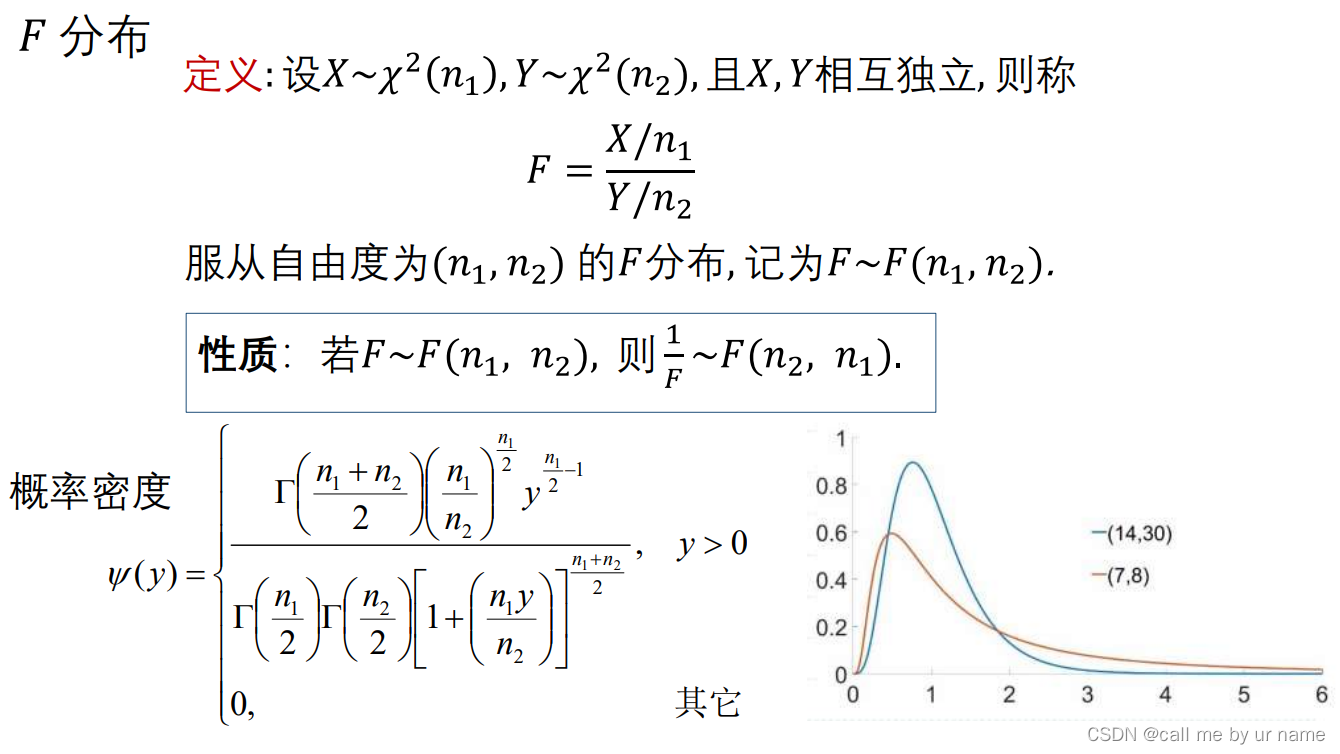
由2个 相互独立 的卡方分布组成
分子，分母都是卡方分布除以自由度
F倒数，将里面的顺序交换

性质

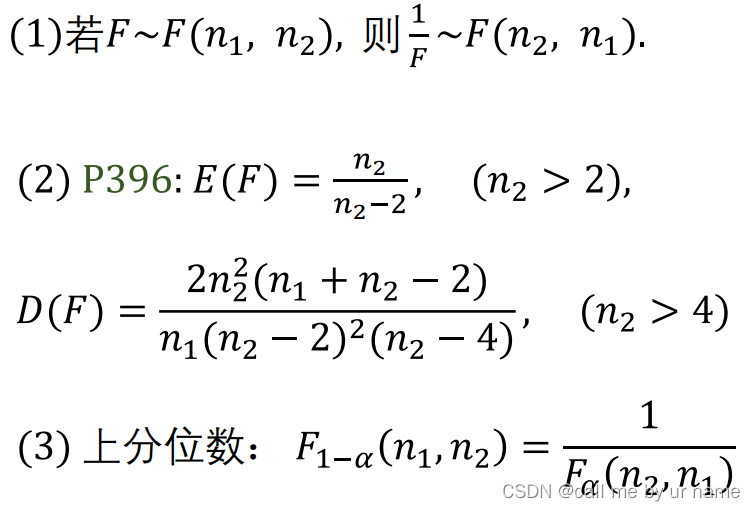
抽样定理

练习

写这道题真的不熟练
很难写
联合=（全部）边缘的乘积
10个人的平均值=10个人的分数和/10此时，服从正态分布。因为10个人是样本，相互独立，所以相加为正态分布。再求出相加完的正态分布的期望和方差


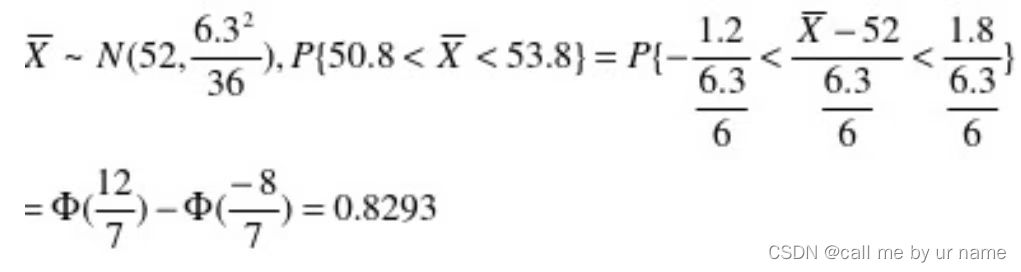
哇，真的不熟啊
看完答案挺简单的
真的需要多练了


样本均值——
总体均值——

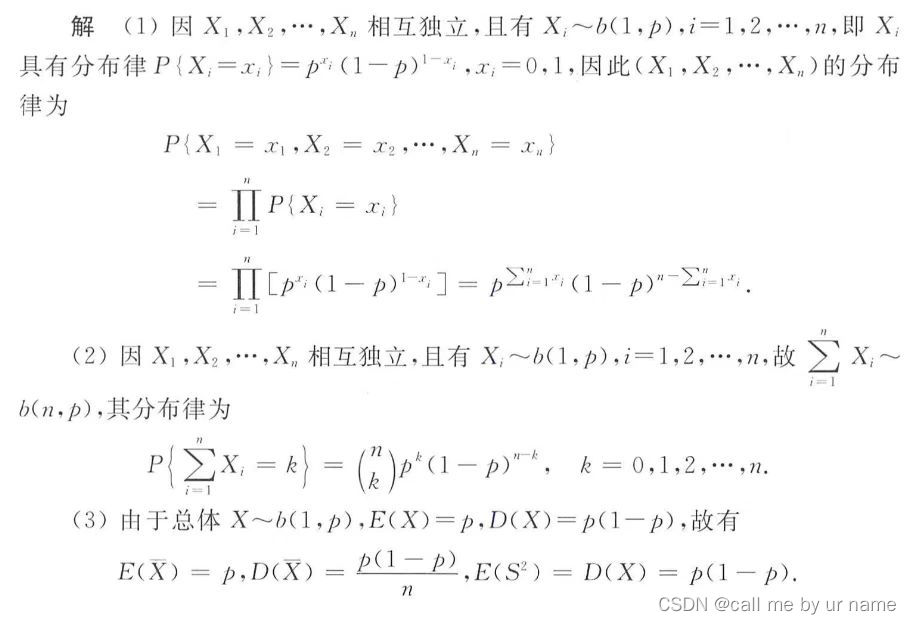
1. 看看第一问的写法
2. 反复熟悉第3问

证明卡方分布

关于上α分位的查表

主要是查表这，因为已经知道了自由度（也就是n）,然后根据n找到最接近30.615的数，再看α，得到概率大小联系上文的公式