哈夫曼编码

简介

哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码（有时也称为霍夫曼编码）。

发展历史

1951年，哈夫曼和他在MIT信息论的同学需要选择是完成学期报告还是期末考试。导师Robert M. Fano给他们的学期报告的题目是，寻找最有效的二进制编码。由于无法证明哪个已有编码是最有效的，哈夫曼放弃对已有编码的研究，转向新的探索，最终发现了基于有序频率二叉树编码的想法，并很快证明了这个方法是最有效的。由于这个算法，学生终于青出于蓝，超过了他那曾经和信息论创立者香农共同研究过类似编码的导师。哈夫曼使用自底向上的方法构建二叉树，避免了次优算法Shannon-Fano编码的最大弊端──自顶向下构建树。

1952年，David A. Huffman在麻省理工攻读博士时发表了《一种构建极小多余编码的方法》（A Method for the Construction of Minimum-Redundancy Codes）一文，它一般就叫做Huffman编码。

Huffman在1952年根据香农（Shannon）在1948年和范若（Fano）在1949年阐述的这种编码思想提出了一种不定长编码的方法，也称霍夫曼（Huffman）编码。霍夫曼编码的基本方法是先对图像数据扫描一遍，计算出各种像素出现的概率，按概率的大小指定不同长度的唯一码字，由此得到一张该图像的霍夫曼码表。编码后的图像数据记录的是每个像素的码字，而码字与实际像素值的对应关系记录在码表中。

赫夫曼编码是可变字长编码(VLC)的一种。 Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长 度最短的码字，有时称之为最佳编码，一般就称Huffman编码。下面引证一个定理，该定理保证了按字符出现概率分配码长，可使平均码长最短。

思想

对于更高频的符号，使用更短的编码。这样在对整个信息进行编码时，就可以进行大幅度压缩。

示例

比如一段英文字符AABABCABAB。其中，A出现了5次，B出现了4次，C出现1次。如果我们使用定长编码来进行信息编码，那么每个符号至少需要2个bit来表示：A（01）, B（10）, C（11），那么字符的编码长度=52+42+1*2 =20bit。但如果采用哈夫曼编码，对于出现频次更高的A，可以使用更短的编码。这里通过构造哈夫曼树来生成码字：

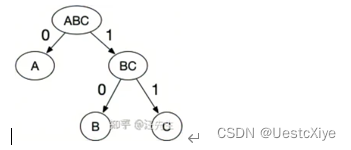
于是，A（0），B（10），C（11），整段字符的编码长度=51+42+1*2=15bit。可以看见采用哈夫曼编码后，有效的对信息进行了压缩。

不足

哈夫曼确实可以对数据进行压缩，但是无法逼近香农提出的熵极限。对于上面提出的【A出现了5次，B出现了4次，C出现了1次】这种情况，每种符号出现的概率如下：P(A) = 0.5，P(B) = 0.4，P© = 0.1。按照香农的熵计算公式，整个信息的熵应该是：

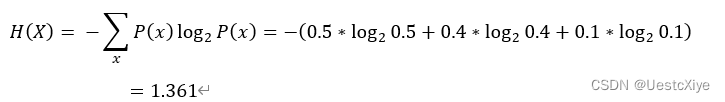
也就是这段字符的压缩极限为，平均每个符号用1.361个bit表示。整段字符一共10个字母，压缩极限为10*1.361=13.61bit≈14bit，而采用哈夫曼编码时，我们只压缩到了15bit。为什么会这样呢？这是因为哈夫曼是采用整数进行符号编码的，不够精准，比如对于上面的B和C，它们出现的概率分别为0.4和0.1，但是对于它们俩，哈夫曼却采用了相同长度的编码。