第15章 基数法则
15.1 通过其他计数来计算当前计数
如何计算拥挤的房间里有多少人?你可以数人头,因为一个人就只有一个头。或者,也可以数耳朵,然后除以2。我们往往可以通过对其他事物计数进而计算当前计数。
最直截了当的通过查找一种事物来确定另一种事物的方式,是发现它们之间的双射。因为如果它们之间有双射的关系,那么数目肯定是一样的。这个重要的现象叫作双射规则/双射法则。
15.1.1 双射规则
双射规则就像是计算能力的放大器,如果你弄明白了一个集合的数目,那么就能通过双射的方式立刻测定出其他集合的大小。
例:
A=当5种类型的甜甜圈都能挑的情况下,挑出12个甜甜圈的所有方式。
B=所有正好有4个1的16-bit序列。
我们可以用以下方式表示A中的一个集合

消去空白后:
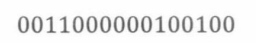
我们得到了一个集合B的元素,这表明A和集合B之间存在一个双射。
因此由双射法可知,|A| = |B|。
引理15.1.1:有k种口味,选出n个甜甜圈的方式的数目,和n个0,(k-1 )个1的序列的数目一样。
15.2 序列计数
双射法则能够从一个计数得到另一个计数。这表明了一个常规的策略:首先仅对几样东西进行计数,然后用双射来得出所有东西的数目!
15.2.1 乘积法则
乘积法则为我们提供了乘积的大小的集合。我们学过,如果 P 1 , P 2 . . . . , P n P_1,P_2....,P_n P1,P2....,Pn是集合,那么
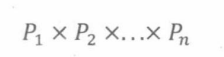
就是第一项取自 P 1 P_1 P1、第二项取自 P 2 P_2 P2、第n项取自 P n P_n Pn的所有可能情况的集合。
法则15.2.1:(乘积法则,product rule )如果 P 1 , P 2 . . . . , P n P_1,P_2....,P_n P1,P2....,Pn是无限集,那么:
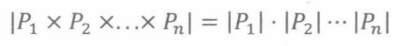
15.2.2 n-元素集合的子集
定理4.5.5通过构建一个子集到长度为n的比特字符串之间的双射,证明了一个n-元素集合一共有 2 n 2^n 2n个子集。现在我们可以解释为什么会有2"个长度为n的比特字符串了,将所有n比特序列的集合写作集合的积:
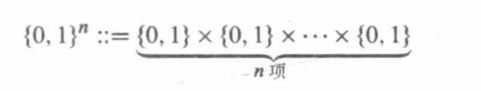
然后,乘积法则给了我们答案:
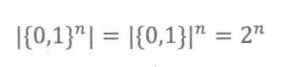
15.2.3 加和法则
法则15.2.2:(加和法则)如果 A 1 , A 2 . . . . A n A_1,A_2....A_n A1,A2....An是不相交的集合,则:
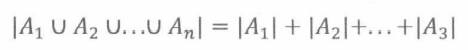
注意,加和法则只适用于不相交集合的并集。
15.2.4 密码计数
很少有计数问题只通过单一法则即可解决。通常,解决方案需要混合使用加和、乘积、双射及其他方法。
在某个计算机系统中,有效密码是6到8个字符的序列,第一个符号必须是一个字母(可以是小写或大写),其他的符号必须要么是字母要么是数字。那么有多少种不同的密码组合呢?
我们定义两个集合,分别表示第一个有效字符以及后续位置的有效字符:
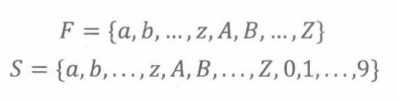
那么,所有可能的密码的集合是:


15.3 广义乘积法则
要把诺贝尔奖、日本奖和普利策奖颁给n个人,有多少种颁法?这个问题结果非常简单,答案为 n 3 n^3 n3,但是,如果这三个奖项必须颁发给不同的学者呢?
集合P表示n个人拿一个奖,集合S如下
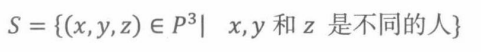
集合S到奖项分配之间存在一个双射。
这样,原始问题就简化为一个序列计数问题。但是,应用乘积法则不能直接对这种类型的序列进行计数,因为这些项之间是相互依赖的,它们必须各不相同。不过有一个巧妙的工具可以解决这个问题。
法则15.3.1:(广义乘积法则,Generalized Product Rule )设S是长度为k的序列构成的集合。如果存在:

因此,根据广义乘法法则,以上问题中 |S| = n ·(n-1)·(n-2)
15.3.1 有缺陷的美元钞票
如果美元钞票的8位序列号中出现重复数字,那么它是有缺陷的( defective )。

分母直接用乘积法则,分子用广义乘积法则。求得结果如下:

15.3.2 一个象棋问题
问题:在8 x 8的棋盘中放置3个棋子,使其存在于不同的行和列,一共有多少种放法?
首先,我们将这个棋子问题映射成一个序列问题。从摆放配置到序列存在一个双射:
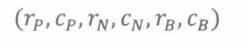

15.3.3 排列
集合S的排列是指S中的每一个元素刚好出现一次而构成的序列
一个n-元素集合有 n ! n! n!种排列。
15.4 除法法则
k对1函数将域( domain )中的k个元素映射到各个元素的陪域。例如,将每只耳朵映射到它的主人的函数是2对1的。
法则15.4.1:(除法法则) 如果f:A→B是k对1的,那么|A|= k·|B|。
其实很多计数问题都是先对单个项进行多次计数,然后使用除法法则更正答案,从而简化问题。我们来看一些例子。
15.4.1 另一个象棋问题
在棋盘上摆放两辆相同的车确保它们不在同一行或同一列,有多少种不同的摆放配置?
设A表示序列( r 1 , c 1 , r 2 , c 2 r_1, c_1, r_2, c_2 r1,c1,r2,c2)的集合,其中 r 1 r_1 r1和 r 2 r_2 r2是不同的行, c 1 c_1 c1和 c 2 c_2 c2是不同的列。
设B表示有效的车位置配置集合。从集合A到集合B存在一个自然函数f。
但现在有一个问题。考虑序列: (1,a,8,h)和 (8,h,1,a)是相同的配置。函数f将两个不同的序列映射到一个相同的棋盘摆放策略,即f是一个2对1的函数。因此,根据除法法则,|A|=2·|B|,调整可得:
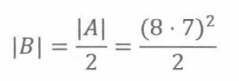
15.4.2 圆桌骑士
亚瑟王要将n个不同的骑士安排在圆桌就座,一共有多少种坐法呢?如果两次排座对应的序列——从序号为1的骑士开始,沿桌子顺时针方向得到的骑士序列——相同,那么这两次排座是同一个安排。
将排座定义为:从正上方的骑士开始,沿桌子顺时针方向得到的骑士序列。因此,排座对应骑士的排列,共有n!种排列。
但是会有重复的情况发生,例如,如果n = 4,那么以下4个不同的序列对应同一种安排。
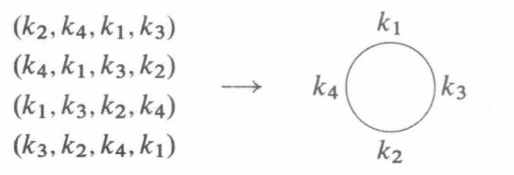
实际上,从排座到安排的映射是一个n对1的函数,因为座位图上的所有骑士按顺序进行n次循环位移,得到同一种安排方式。因此,根据除法法则,圆桌就座安排方法的个数是:
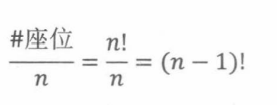
15.5 子集计数
一个n-元素集合包含多少个k-元素子集呢?
由于这类数字经常出现,所以它有一个特殊的标记:

15.5.1 子集法则
我们可以使用除法法则为n选k的计数问题推导出一个简单的公式。方法是:对n-元素集合{ a 1 , . . . . . , a n a_1,.....,a_n a1,.....,an}任意排列,取其前k个元素,可得到一个k-元素子集。即,将排列 a 1 , . . . . . , a n a_1,.....,a_n a1,.....,an映射到集合{ a 1 , a 2 . . . a k a_1 , a_2...a_k a1,a2...ak}。
注意,对任意排列来说,只要前k个元素 a 1 , a 2 . . . a k a_1 , a_2...a_k a1,a2...ak相同,不论元素顺序如何,也不论其他n - k个元素的顺序如何,都会映射到这个集合。。换句话说,这个到k-元素子集的映射是k! (n 一k)!对1的。
我们知道,一个n-元素集合有n!种排列,因此根据除法法则,得出
从而证明了:
法则15.5.1(子集法则,Subset Rule )一个n-元素集合包含
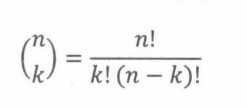
个k-元素子集。
15.5.2 比特序列
恰好包含k个1的n-比特序列有多少个?我们已经知道, n-元素集合与n-比特序列之间存在双射关系。
推论15.5.2:恰好包含k个1的n-比特序列的数目是 ( n k ) \dbinom{n}{k} (kn)。
此外,由引理15.1.1风味甜甜圈与比特序列之间的双射关系可知。
推论15.5.3:假定有k种口味,选择n个甜甜圈的方案个数是 ( n + ( k − 1 ) n ) \dbinom{n+(k-1)}{n} (nn+(k−1))
15.6 重复序列
15.6.1子集序列
设A是一个n-元素集合, k 1 , k 2 . . . . k m k_1,k_2.... k_m k1,k2....km都是非负整数且和为n。A的 ( k 1 , k 2 . . . . , k m ) (k_1,k_2.... , k_m) (k1,k2....,km)-分割由以下序列表示: ( A 1 , A 2 . . . . . A m ) (A_1,A_2. ... . A_m) (A1,A2.....Am)
其中 A i A_i Ai是A的互不相交的子集,且 ∣ A i ∣ = k |A_i|=k ∣Ai∣=k ,i=1… m。
这是一个从n!个排列到 ( k 1 , k 2 . . . . k m ) (k_1,k_2.... k_m) (k1,k2....km)-分割的映射,是一个 k 1 ! k 2 ! . . . k m ! k_1! k_2!...k_m! k1!k2!...km!对1的函数,因此根据除法法则,可得子集分割法则( Subset Split Rule )。
定义15.6.1:对于n, k 1 . . . k m k_1...k_m k1...km ∈ N,有 k 1 + k 2 + . . . + k m = n k_1+ k_2+...+k_m = n k1+k2+...+km=n,定义多项式系数为
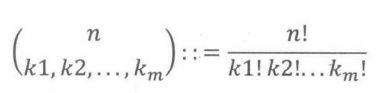
15.6.2 Bookkeeper 法则
给定一个长度为10的单词BOOKKEEPER,通过字母排列可以生成多少个序列?
BOOKKEEPER中有一个B,两个0,两个K,三个E,一个P和一个R。所以,BOOKKEEPER的排列与集合{1,2…10}的(1,2,2,3,1,1)-分割之间存在双射关系。即,将排列映射成这样的序列:序列的每个元素表示不同字母在排列中出现的位置。
例如,在排列 BOOKKEEPER 中,B在第1个位置,0出现在第2、3个位置,K在第4、5个位置,E在第6、7、9个位置,Р在第8个位置,以及R在第10个位置。所以BOOKKEEPER的映射是
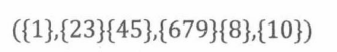
由子集分割法则,我们可以推断出单词BOOKKEEPER的字母重排总数为:
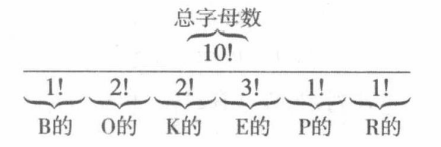
法则15.6.3( Bookkeeper法则):设 l 1 , . . . , l m l_1,...,l_m l1,...,lm是不同的元素, l 1 l_1 l1出现 k 1 k_1 k1次, l 2 l_2 l2出现 k 2 k_2 k2次,……, l m l_m lm出现 k m k_m km次,对应的序列个数是:
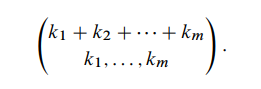
15.6.3 二项式定理
定理15.6.4(二项式定理 ):对于所有n ∈ N和a, b ∈R:
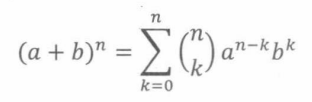
关于二项式的推理很容易扩展到多项式 ( multinomial ),即两个或更多项的和。例如,求多项式 ( b + o + k + e + p + r ) 1 0 (b+o+k +e+p +r)^10 (b+o+k+e+p+r)10展开项
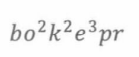
的系数。这个多项式展开的每一项是b,o,k, e,p或r中的一个或多个构成的10 个变量的乘积。 b o 2 k 2 e 3 p r bo^2k^2e^3pr bo2k2e3pr中有1个b,2个o,2个k,3个e,1个p和1个r。因此,这项的系数是这些变量的BOOKKEEPER重排数目:
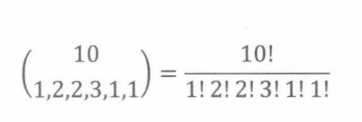
定理15.6.5(多项式定理 ):对于所有n ∈ N,
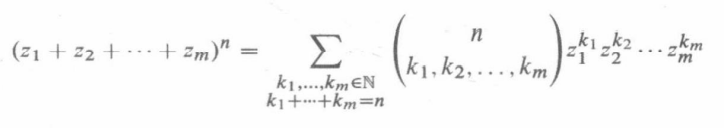
15.7计数练习:扑克手牌
玩一个抽五张牌的纸牌游戏,每个玩家从一副52张牌的纸牌中抽取5张。0五张牌的数目等于从一个52-元素集合中挑选一个5-元素子集,即:
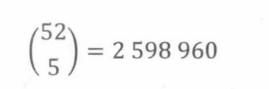
下面我们做几个计数练习,指定手牌的不同属性进行5张牌计数。
15.7.1四条相同点数的手牌
四条是指其中四张是相同点数但不同花色的手牌。带四条的五张手牌有多少个?
同样,第一步是将这个问题映射到序列计数问题。四张相同点数的五张牌计数可以描述为以下序列:

因此,这个问题可以映射为两个点数和一个花色构成的序列。

现在我们只需要对序列进行计数即可。第一个点数有13种选择,第二个点数有12种选择,花色有4种选择。因此,根据广义乘法法则,四张相同点数的五张牌有13·12-4=624种。
15.7.2 葫芦手牌
葫芦( Full House)是指三张牌是一个点数、其他两张牌是另一个点数。
再次将这个问题转换成序列问题。葫芦与序列之间存在以下双射关系:


根据广义乘积法则,葫芦的数量是:
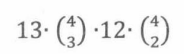
15.7.3两个对子的手牌
含有两个对子的手牌有多少种?
两个对子的手牌可以描述成以下序列:

也就是说,可能出现两个对子手牌的个数是:
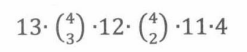
这是错误的答案!问题出在两个对子手牌与上述序列之间不是双射关系。实际上这是一个二对一的映射。

这里,序列数量是手牌的两倍,所以根据除法法则,实际上两个对子的手牌数量是:
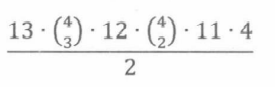
对于以上问题,有两种应对方法:
1.凡是采用映射f:A→B将一个计数问题转换成另一个计数问题的时候,就要检查A中多少个(相同数量)元素映射到B的每个元素。假设A中的k个元素映射到B的每一个元素,那么根据除法法则除以常数k。
2.除此之外,尝试采用不同的方法来解决同样的问题。通常来说,方法不止一种,而且所有方法都可以得出相同的答案!
15.7.4花色齐全的手牌
这种手牌可以描述成以下序列:


还有没有别的序列对应这副手牌?
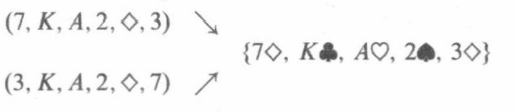
因此,花色齐全的手牌总数是:

15.8鸽子洞原理
鸽子洞原理
如果鸽子比洞多,那么至少有两只鸽子一定在同一个洞里。
法则15.8.1(鸽子洞原理):如果|A|> |B|,则对于全函数f:A →B,A一定存在两个不同元素通过f映射到B的同一个元素。
应用鸽子洞原理解决问题的时候,关键是要搞清楚三件事:

15.8.1头上的头发
法则15.8.2(广义鸽子洞原理)如果|A| > k ·|B|,则对于全函数f :A →B,A存在至少k +1个不同元素通过f映射到B的同一个元素。
例:例如,随机挑选两个人,他们头上的头发数量肯定不会完全相同。但在马萨诸塞州波士顿,存在三个人的头发数量完全相同!
波士顿大约有50 万人不秃头,而且最多的有20 万根头发。设A是波士顿不秃头的人,B={10 000,10 001,…,200 000},f是这个人到他的发量的映射。由于|A>2|B|,根据广义鸽子洞原理,至少有三人拥有相同数量的头发。
15.8.2具有相同和的子集
给出了90个25位数。在这些25位数中,是否存在具有相同和的两个不同子集?
虽然找到这样两个集合很困难,但是我们可以用鸽子洞原理证明这两个子集存在。
设A表示90个数的所有子集构成的集合。由于一共只有90个数,而且任一25位数小于 1 0 25 10^{25} 1025,因此任意一个子集的和最多是 90 ⋅ 1 0 25 90·10^{25} 90⋅1025。设B是整数集合{0,1… 90 ⋅ 1 0 2 5 90· 10^25 90⋅1025}, f将每一个子集(A)映射到它的和(B )。
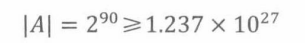
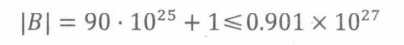
这两个数量都很庞大,但|A|略大于|B。这意味着f将A的至少两个元素映射到了B的同一个元素。换句话说,根据鸽子洞原理,两个不同的子集一定具有相同的和!
注意,这个证明并没有指出哪两个集合具有相同的和,这称为非构造性证明。
15.8.3魔术
魔术师让助手给观众一副52张牌的扑克,而魔术师自己不看。
5名观众每人从中选择一张牌。然后,助手收集这5张牌,将其中的4张牌展示给魔术师。然后,魔术师很快就正确地猜出了第5张牌!
15.8.4秘密
助手能够准确地透露第5张牌,应用的方法正是计数和匹配。
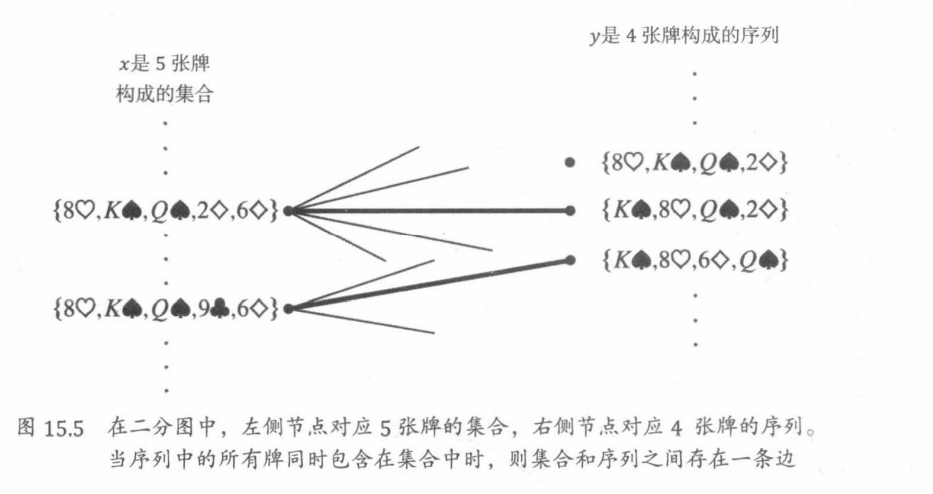
如上图,魔术师和助手面临的实际上是一个二分匹配的问题。
左边的每一个顶点对应助手的信息,即5张牌的集合。因此,左边顶点的集合X包含(52)个元素。
右边的每个顶点对应魔术师的信息,即4张牌的序列。所以右边顶点的集合Y有52·51·50·49个元素。
对于左边的顶点,选择隐藏―张牌有5个方案,剩余4张牌有4!种排列,因此左侧每个顶点的度120。
对于右边的顶点,第5张牌有48种选择,因此右侧每个顶点的度为48。根据定义12.5.5,这个图是带有度约束的,因此根据定理12.5.6存在匹配。
15.8.5真正的秘密
魔术师和他的助手需要商量一种匹配方式,这听起来是非常好的,但他们怎样才能记住(52)= 2598 960条边的匹配关系呢?
这里我们介绍一种方法。例如,假设观众选择:

1、助手选择同样花色的2张牌。
2、助手确定这两张牌的点数,按照顺着时针方向,他们之间的距离总是在1到6之间
3、逆时针方向最远位置的牌最先展示,那么另一张则成为秘密牌。
因此:

4、接下来需要确定1到6之间的一个数字。魔术师和助手事先商量好一种排序,比如从小到大顺序为:

后三张牌的展示顺序按如下方式定义:

15.8.6 如果是4张牌呢
假设观众只选择4张牌,助手向魔术师展示3张牌。魔术师能知道第4张牌是什么吗?
设X表示观众选择的四张牌集合,Y表示助手展示的三张牌序列。
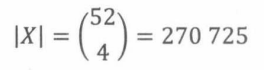

因此,根据鸽子洞原理,展示相同的3张牌序列至少需要

种不同的四张牌手牌。这对魔术师来说是一个坏消息:如果他看到了3张牌序列,那么第4张牌至少存在3种无法区分的情形。
15.9容斥原理
集合的并集有多大?给定三个集合M、E、P,根据加法法则,如果集合不相交,那么他们的和是
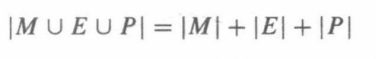
但是,如果三个集合相交该如何创建并集呢?
15.9.1 两个集合的并集
给定两个集合S,和S2,容斥原理是指它们的并集的大小是:
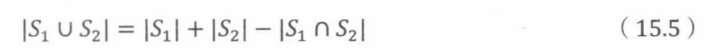
15.9.2 三个集合的并集
三个集合的并集大小可由更复杂的容斥原理计算:
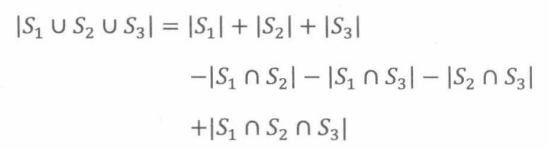
15.9.3 42序列、04序列或60序列
在集合{0,1,2…}中,有多少种排列是4、2,或0、4,或6、0连续出现的?
首先,必须确定单个集合(如 P 60 P_{60} P60)的大小。我们可以用一个小技巧:将6和0组合在一起看成单个符号。那么,存在以下双射关系
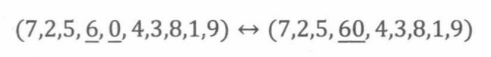
所以,| P 60 P_{60} P60|= 9!。同理,| P 04 P_{04} P04|=| P 42 P_{42} P42|= 9!。
同理,也可以去计算交集的大小为 ∣ P 42 ∣ ∩ ∣ P 60 ∣ = 8 ! |P_{42}|\cap |P_{60}| = 8! ∣P42∣∩∣P60∣=8!、 ∣ P 04 ∣ ∩ ∣ P 60 ∣ = 8 ! |P_{04}|\cap |P_{60}| = 8! ∣P04∣∩∣P60∣=8!、 ∣ P 42 ∣ ∩ ∣ P 04 ∣ = 8 ! |P_{42}|\cap |P_{04}| = 8! ∣P42∣∩∣P04∣=8!、 ∣ P 42 ∣ ∩ ∣ P 60 ∣ ∩ ∣ P 04 ∣ = 7 ! |P_{42}|\cap |P_{60}|\cap |P_{04}| = 7! ∣P42∣∩∣P60∣∩∣P04∣=7!
带入以上公式的得到:
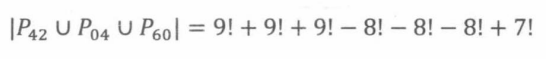
15.9.4 n个集合的并集
单个集合大小的和,有一个简洁的标记表示,
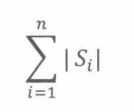
“两个集合的交集”表示为 S i ∩ S j S_i \cap S_j Si∩Sj,其中i ≠ j。
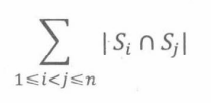
同理,三个集合交集的大小是:
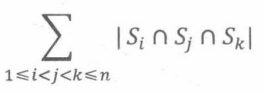
在容斥原理中,这些和项的正负符号是交替出现的, k个集合交集的符号是 ( − 1 ) k − 1 (-1)^{k-1} (−1)k−1。因此,容斥原理的公式表达为:
法则(容斥原理)
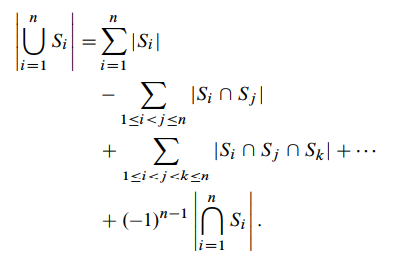
虽然这种和项的和形式很方便地表述了容斥原理,但其实没有必要把多少个集合的交集逐个列出来。另一种写法是:
法则(容斥原理-II )
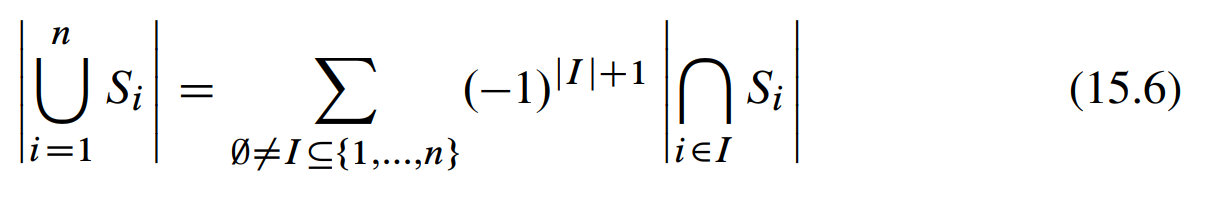
15.9.5计算欧拉函数
利用容斥原理可以证明推论9.10.11的欧拉函数公式:

首先,设S表示[0…n)中不与n互质的整数集合。所以 ϕ ( n ) = n − ∣ S ∣ \phi(n)=n - |S| ϕ(n)=n−∣S∣。然后,设 C a C_a Ca是[0…n)中能被a整除的整数集合,即:

所以,S中的整数刚好就是[0…n)中能被至少一个 p i p_i pi整除的整数。也就是说,

所以:
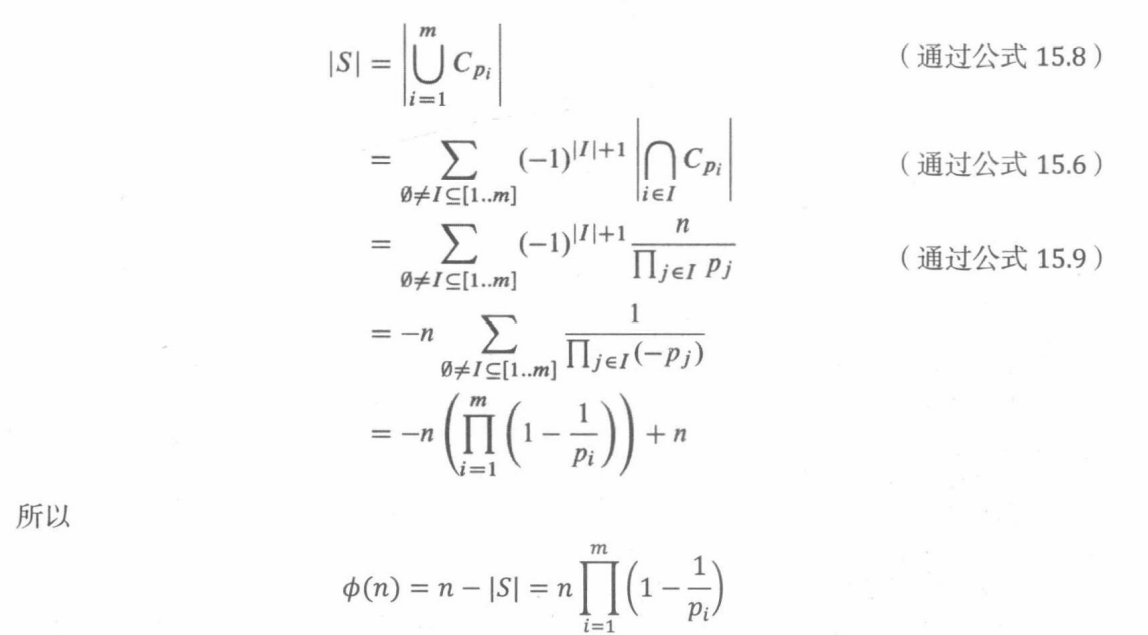
15.10 组合证明
假设现在有n件不同的T恤,只保留k件。你可以同等地选择k件留下,或选择补集n 一k件丢掉。因此:
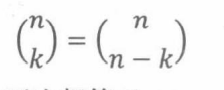
15.10.1 帕斯卡三角恒等式
在n个人中竞选k个人,Bob也想要成为k个人中的一员,首先他要弄清楚一共有多少种可能的队伍。
Bob被选上,他的k -1个队友是从其他n 一1个克争对于中挑选出米的。这什组建的队伍数量是:
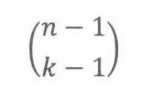
Bob没有被选中,所有k个队员都是从其他n-1个竞争对手中选出来的。这时组建的队伍数量是:
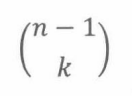
两个集合不相交,所以队伍总数是:
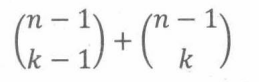
另一种推理方法,n个人(包括他自己)竞争k个位置,那么选择队伍的可能是:
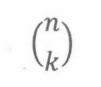
以上两个答案相等,所以
引理15.10.1(帕斯卡三角恒等式 )
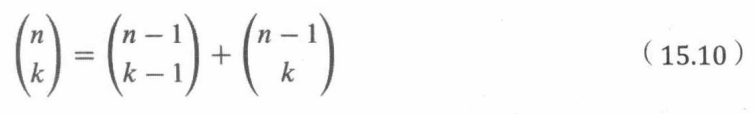
15.10.2 给出组合证明
组合证明是一种依靠计数原理构建代数事实的证明方法。 这种证明大多遵循以下基本框架:
- 定义一个集合S。
- 通过一种计数方式得出|S| =n。
- 通过另一种计数方式得出|S| = m。
- 得出结论:n = m。
检查组合证明
组合证明通过不同的方式对同一件事进行计数。如果已经熟练掌握了不同的计数方法,当然没什么问题;如果还有疑问,可以通过双射和序列计数对组合证明进行检查。
15.10.3有趣的组合证明
组合证明中的其他计数方式通常是基于简单的序列或集合定义的。这里我们给出一个有趣的组合证明例子。
定理15.10.2:
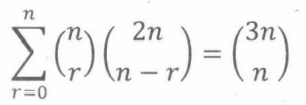
证明.font>我们给出组合证明。设S是从n张不同的红牌、2n张不同的黑牌中选出n张牌的所有手牌集合。首先注意,一个3n-元素集合有
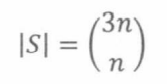
个n-元素子集。
另一方面,刚好有r张红牌的手牌数量是
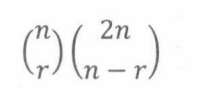
因为r张红牌有 ( n r ) \dbinom{n}{r} (rn)种选择,n -r张黑牌有 ( 2 n n − r ) \dbinom{2n}{n-r} (n−r2n)种选择。因为红牌的数量可以是0到n的任意一个,因此n张手牌的总数是:
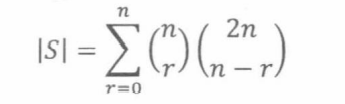
两个|S|相等,证毕。
确定组合证明
red’>可以通过双射和序列计数对组合证明进行检查。
15.10.3有趣的组合证明
组合证明中的其他计数方式通常是基于简单的序列或集合定义的。这里我们给出一个有趣的组合证明例子。
定理15.10.2:
[外链图片转存中…(img-kseWHYjj-1670047080162)]
证明.font>我们给出组合证明。设S是从n张不同的红牌、2n张不同的黑牌中选出n张牌的所有手牌集合。首先注意,一个3n-元素集合有
[外链图片转存中…(img-wxiRbC8Q-1670047080162)]
个n-元素子集。
另一方面,刚好有r张红牌的手牌数量是
[外链图片转存中…(img-IeGAIsOF-1670047080163)]
因为r张红牌有 ( n r ) \dbinom{n}{r} (rn)种选择,n -r张黑牌有 ( 2 n n − r ) \dbinom{2n}{n-r} (n−r2n)种选择。因为红牌的数量可以是0到n的任意一个,因此n张手牌的总数是:
[外链图片转存中…(img-UVSzXHYO-1670047080164)]
两个|S|相等,证毕。
确定组合证明
组合证明可以说是很神奇的。定理15.10.2看起来相当可怕,但我们在证明它的过程中并没有使用任何代数运算。构建组合证明的关键是正确地选择集合S,这可能比较难。一般来说,公式中较简单的那一边可能提供一些提示。




![[附源码]Python计算机毕业设计Django基于Java的图书购物商城](https://img-blog.csdnimg.cn/75a75284f55246019277cdc82bd71054.png)