【计算机图形学】曲线和曲面（Bezier曲线 Bezier曲面）

news2024/11/18 6:26:34

模块5 曲线和曲面

一 实验目的

  1. 编写曲线和曲面的算法

二 实验内容

1：绘制Bezier曲线，并采用自行设计输入和交互修改数据点的方式。

实验结果如下图所示：

第一步：输入特征多边形的顶点个数，并按照顺序输入顶点的坐标。


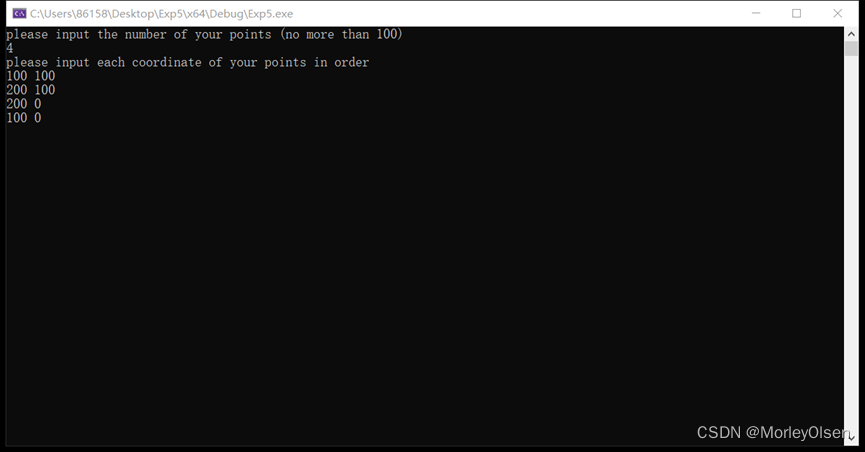
第二步：点击左键生成bezier曲线（白色部分）和多边形顶点（绿色部分）。

 


第三步：点击右键修改顶点，首先输入需要修改的顶点在数组中的坐标（即顺序个数-1），此处以（100，100）为例，将其修改为（100，300）。


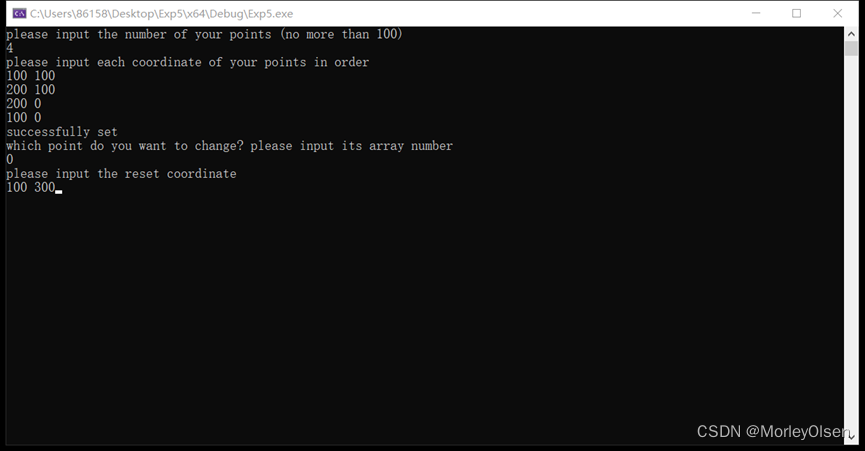
第四步：通过敲击回车键，可观察修改后的bezier曲线和顶点。

 

第五步：如果需要继续修改顶点坐标，用户可以继续点击右键，重复上述操作。此处不再赘述。如果需要退出图像绘制界面，用户可以通过敲击esc键，即可退出本实验界面。

2：绘制Bezier曲面，双三次类型。


实验结果如下图所示：

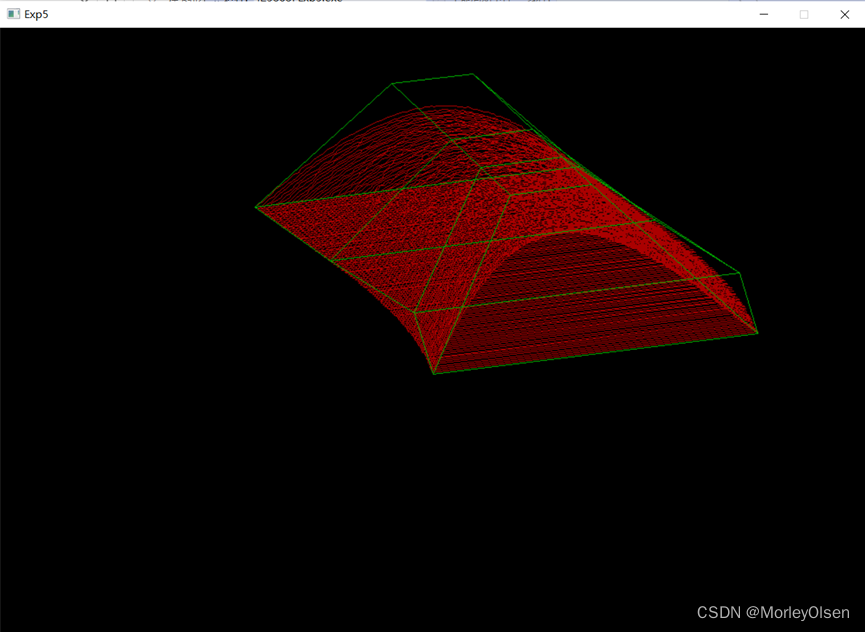
2.1：绘制Bezier曲面，并采用自行设计输入和交互修改数据点的方式，改进。


实验结果如下图所示：


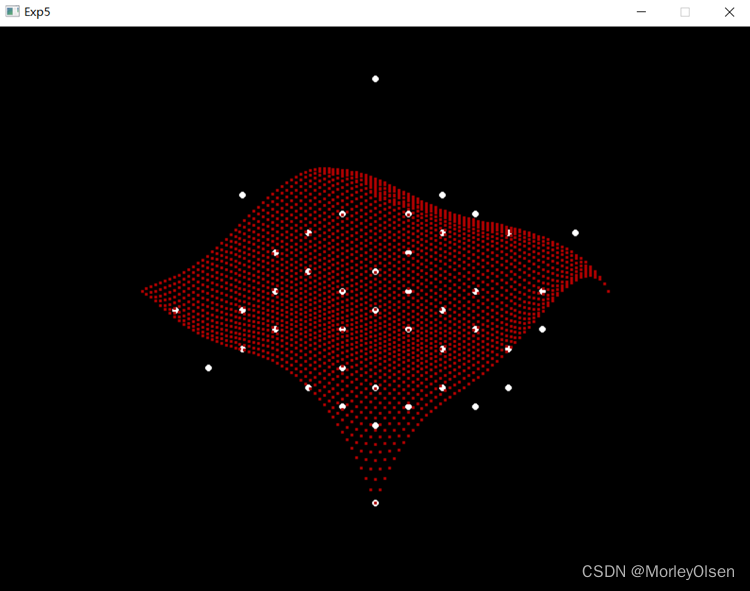
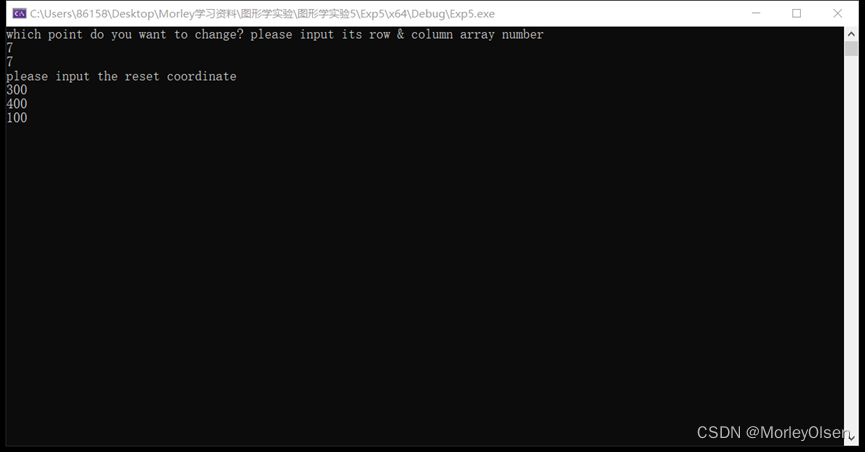
修改数据点：

 

新贝塞尔曲面：

三 程序说明

最终的实验代码如下表所示：

1题

//

// 程序名称：Bezier曲线

// 功    能：绘制Bezier曲线，并采用自行设计输入和交互修改数据点的方式。

// 编译环境：VS2019，EasyX_20220116

// 最后修改：2022-4-28

#include <graphics.h>

#include <conio.h>

#include <iostream>

#include <math.h>

using namespace std;

//特征多边形的特征

int n;

int px[100], py[100];

//初始化特征多边形

void initialize() {

    cout << "please input the number of your points (no more than 100)" << endl;

    cin >> n;

    cout << "please input each coordinate of your points in order" << endl;

    for (int i = 0; i < n; i++) {

         cin >> px[i] >> py[i];

    }

    cout << "successfully set" << endl;

}

//递归

int Factorial(int nn) {

    if (nn == 0 || nn == 1) return 1;

    else return nn * Factorial(nn - 1);

}

//绘制bezier曲线

void Bezier() {

    int nn = n - 1;

    //line(px[0], py[0], px[1], py[1]);

    double i = 0, n1, n2;

    n1 = Factorial(nn);

    moveto(px[0], py[0]);

    POINT point;

    //在[0,1]内循环

    for (; i <= 1; i += 0.01) {

         point.x = 0;

         point.y = 0;

         for (int j = 0; j <= nn; j++) {

             n2 = (n1 / (Factorial(j) * Factorial(nn - j))) * pow(i, j) * pow(1 - i, nn - j);

             point.x += n2 * px[j];

             point.y += n2 * py[j];

         }

         lineto(point.x, point.y);

    }

    lineto(px[n - 1], py[n - 1]);

    //描绘用户定义的点

    for (int ii = 0; ii < n; ii++) {

         setfillcolor(GREEN);

         fillcircle(px[ii], py[ii], 3);

    }

}

//主函数

int main() {

    //初始化

    initialize();

    initgraph(640, 480);

    ExMessage m;

    //绘制图像

    while (1) {

         m = getmessage(EX_MOUSE | EX_KEY);

         switch (m.message) {

             //右键修改坐标信息

             case WM_RBUTTONDOWN:

                  closegraph();

                  int arr, newx, newy;

                  //输入数组中的坐标，进行修改

                  cout << "which point do you want to change? please input its array number" << endl;

                  while (1) {

                      cin >> arr;

                      if (arr >= n) {

                          cout << "input error, try again" << endl;

                      }

                      else {

                          break;

                      }

                  }

                  cout << "please input the reset coordinate" << endl;

                  cin >> newx >> newy;

                  px[arr] = newx;

                  py[arr] = newy;

                  cout << "successfully reset, please wait a second to see a new graph" << endl;

                  initgraph(640, 480);

             //左键绘制

             case WM_LBUTTONDOWN:

                  Bezier();

             //退出图形化界面

             case WM_KEYDOWN:

                  if (m.vkcode == VK_ESCAPE) {

                      return 0;

                  }

         }

    }

    _getch();

    closegraph();

    return 0;

}

2题

//

// 程序名称：Bezier曲面

// 功    能：绘制Bezier曲面，双三次类型。

// 编译环境：VS2019，EasyX_20220116

// 最后修改：2022-5-9

#include <graphics.h>

#include <conio.h>

#include <iostream>

#include <cmath>

using namespace std;

#define pi 3.1415926

#define MAX 20

//三维点类

class Point3D {

public:

    double x, y, z;

    Point3D(int x = 0, int y = 0, int z = 0) {

         this->x = x;

         this->y = y;

         this->z = z;

    };

    void operator=(Point3D& a) {

         x = a.x;

         y = a.y;

         z = a.z;

    };

    Point3D operator*(double a) {

         return Point3D(a * x, a * y, a * z);

    };

    Point3D operator+(Point3D a) {

         return Point3D(x + a.x, y + a.y, z + a.z);

    };

    void operator+=(Point3D a) {

         x += a.x;

         y += a.y;

         z += a.z;

    };

};

//求阶乘

long int Factorial(int n) {

    int i, sum = 1;

    if (n == 0) {

         return 1;

    }

    for (i = 2; i <= n; i++) {

         sum *= i;

    }

    return sum;

}

//Bernstein函数

double Bernstein(int i, int n, double t) {

    return (double)Factorial(n) / Factorial(i) / Factorial(n - i) * pow(t, i) * pow(1 - t, n - i);

}

//Bezier曲面求解

void BezierCurve(Point3D p[][MAX], int n, int m, int nd, int md, double sita, double fai) {

    double hu = 1.0 / nd;

    double hv = 1.0 / md;

    double u = 0, v = 0;

    int i, j, k, l;

    sita = sita * pi / 180;

    fai = fai * pi / 180;

    int** pB = new int* [nd + 1];

    for (i = 0; i <= nd; i++) {

         pB[i] = new int[2 * md + 2];

    }

    Point3D ptemp(0, 0, 0);

    for (i = 0; i <= nd; i++, u += hu) {

         v = 0;

         for (j = 0; j <= 2 * md + 1; j += 2, v += hv) {

             ptemp.x = 0;

             ptemp.y = 0;

             ptemp.z = 0;

             for (k = 0; k <= n; k++) {

                  for (l = 0; l <= m; l++) {

                      ptemp += p[k][l] * Bernstein(k, n, u) * Bernstein(l, m, v);

                  }

             }

             pB[i][j] = ptemp.x * cos(sita) - ptemp.y * sin(sita) + 500;

             pB[i][j + 1] = -ptemp.x * sin(sita) * sin(fai) - ptemp.y * cos(sita) * sin(fai) + ptemp.z * cos(fai) + 400;

         }

         drawpoly(md + 1, pB[i]);

    }

    for (i = 0; i < nd + 1; i++) {

         delete[]pB[i];

    }

    delete[]pB;

}

//画控制多边形

void drawControlPoly_3D(Point3D p[][MAX], int n, int m, double sita, double fai, int color) {

    int** p2d = new int* [n + 1];

    int i, j;

    setcolor(color);

    sita = sita * pi / 180;

    fai = fai * pi / 180;

    for (i = 0; i < n + 1; i++) {

         p2d[i] = new int[2 * m + 4];

    }

    char str[80];

    //3D->2D

    for (i = 0; i <= n; i++) {

         for (j = 0; j <= m; j++) {

             p2d[i][2 * j] = p[i][j].x * cos(sita) - p[i][j].y * sin(sita) + 500;

             p2d[i][2 * j + 1] = -p[i][j].x * sin(sita) * sin(fai) - p[i][j].y * cos(sita) * sin(fai) + p[i][j].z * cos(fai) + 400;

         }

         p2d[i][2 * j] = p2d[i][0];

         p2d[i][2 * j + 1] = p2d[i][1];

         drawpoly(m + 2, p2d[i]);

    }

    for (j = 0; j <= 2 * m + 1; j += 2) {

         moveto(p2d[0][j], p2d[0][j + 1]);

         for (i = 1; i <= n; i++) {

             lineto(p2d[i][j], p2d[i][j + 1]);

         }

    }

    for (i = 0; i < n + 1; i++) {

         delete[]p2d[i];

    }

    delete[]p2d;

}

//双几次曲面

void BezierCurve_Shuang(Point3D p[][MAX], int pn, int pm, int nd, int md, double sita, double fai, int shuangjici) {

    int i, j, k, l;

    Point3D point[MAX][MAX];

    for (i = 0; i < pn - shuangjici; i += shuangjici) {

         for (j = 0; j < pm - shuangjici; j += shuangjici) {

             for (k = 0; k <= shuangjici; k++) {

                  for (l = 0; l <= shuangjici; l++) {

                      point[k][l] = p[i + k][j + l];

                  }

             }

             BezierCurve(point, shuangjici, shuangjici, nd, md, sita, fai);

         }

    }

}

//主函数

int main() {

    int n;

    double fai, sita;

    //固定角度了。

    sita = 20;

    fai = 160;

    n = 3;

    //顶点集合

    Point3D p[][MAX] = {

         {Point3D(0,0,0),Point3D(150,150,150),Point3D(250,150,150),Point3D(400,0,0)},

        {Point3D(50,200,0),Point3D(150,250,150),Point3D(250,250,150),Point3D(450,200,0)},

        {Point3D(20,400,0),Point3D(150,350,150),Point3D(250,350,150),Point3D(420,400,0)},

        {Point3D(0,600,0),Point3D(150,550,150),Point3D(250,550,150),Point3D(400,600,0)}

    };

    /*

    cout << "please input sita and fai" << endl;

    cin >> sita >> fai;

    cout << "please input your n" << endl;

    cin >> n;

    */

    //初始化界面

    initgraph(1000, 700);

    setcolor(RED);

    //Bezier曲面

    BezierCurve_Shuang(p, 4, 4, 100, 100, sita, fai, n);

    //画控制多边形

    drawControlPoly_3D(p, 3, 3, sita, fai, GREEN);

    _getch();

    closegraph();

    return 0;

}

2题改进版本

//

// 程序名称：Bezier曲面

// 功    能：绘制Bezier曲面，并采用自行设计输入和交互修改数据点的方式。

// 编译环境：VS2019，EasyX_20220116

// 最后修改：2022-5-13

#include <iostream>

#include <graphics.h>

#include <conio.h>

#include <math.h>

using namespace std;

#define PI 3.1415926

//定义 N * N 的控制点数组

const int N = 8;

float controlPoints[N][N][3] ={

    { {-150, -150, 100}, {-100, -150, 0}, {-50, -150, 0}, {0, -150, 50}, {50, -150, 0}, {100, -150, 0}, {150, -150, -100}, {200, -150, 0} },

    { {-150, -100, 0}, {-100, -100, 50}, {-50, -100, -100}, {0, -100, 0}, {50, -100, 0}, {100, -100, 100}, {150, -100, 0}, {200, -100, -50} },

    { {-150, -50, 0}, {-100, -50, 0}, {-50, -50, 50}, {0, -50, 0}, {50, -50, 0}, {100, -50, 0}, {150, -50, -50}, {200, -50, 0} },

    { {-150, 0, -50}, {-100, 0, -100}, {-50, 0, 0}, {0, 0, 150}, {50, 0, 0}, {100, 0, -100}, {150, 0, -50}, {200, 0, -50} },

    { {-150, 50, 0}, {-100, 50, 0}, {-50, 50, -100}, {0, 50, 0}, {50, 50, 50}, {100, 50, 0}, {150, 50, 0}, {200, 50, 50} },

    { {-150, 100, 50}, {-100, 100, 0}, {-50, 100, 0}, {0, 100, -50}, {50, 100, -50}, {100, 100, 50}, {150, 100, 0}, {200, 100, 0} },

    { {-150, 150, 0}, {-100, 150, 100}, {-50, 150, -100}, {0, 150, 0}, {50, 150, 0}, {100, 150, 0}, {150, 150, -150}, {200, 150, 50} },

    { {-150, 200, 0}, {-100, 200, 0}, {-50, 200, 50}, {0, 200, -50}, {50, 200, 0}, {100, 200, -100}, {150, 200, 0}, {200, 200, 50} }

};

//计算贝塞尔基函数的C值

int C(int n, int k) {

    if (k > n) {

        return 0;

    }

    int c = 1;

    for (int i = 0; i < k; i++) {

        c *= (n - i);

        c /= (i + 1);

    }

    return c;

}

//勾勒函数

void display(float x, float y, float z) {

    putpixel(int(0.7071 * x - 0.7071 * y + 0.5f + 400), int(-0.4082 * x - 0.4082 * y + 0.8165 * z + 0.5f + 300), RED);

    putpixel(int(0.7071 * x - 0.7071 * y + 0.5f + 400) + 1, int(-0.4082 * x - 0.4082 * y + 0.8165 * z + 0.5f + 300), RED);

    putpixel(int(0.7071 * x - 0.7071 * y + 0.5f + 400) - 1, int(-0.4082 * x - 0.4082 * y + 0.8165 * z + 0.5f + 300), RED);

    putpixel(int(0.7071 * x - 0.7071 * y + 0.5f + 400), int(-0.4082 * x - 0.4082 * y + 0.8165 * z + 0.5f + 300) + 1, RED);

    putpixel(int(0.7071 * x - 0.7071 * y + 0.5f + 400), int(-0.4082 * x - 0.4082 * y + 0.8165 * z + 0.5f + 300) - 1, RED);

    putpixel(int(0.7071 * x - 0.7071 * y + 0.5f + 400) + 1, int(-0.4082 * x - 0.4082 * y + 0.8165 * z + 0.5f + 300) + 1, RED);

    putpixel(int(0.7071 * x - 0.7071 * y + 0.5f + 400) + 1, int(-0.4082 * x - 0.4082 * y + 0.8165 * z + 0.5f + 300) - 1, RED);

    putpixel(int(0.7071 * x - 0.7071 * y + 0.5f + 400) - 1, int(-0.4082 * x - 0.4082 * y + 0.8165 * z + 0.5f + 300) + 1, RED);

    putpixel(int(0.7071 * x - 0.7071 * y + 0.5f + 400) - 1, int(-0.4082 * x - 0.4082 * y + 0.8165 * z + 0.5f + 300) - 1, RED);

}

//Bezier曲面绘制

void Bezier() {

    //绘制控制点

    for (int i = 0; i < N - 1; i++) {

        for (int j = 0; j < N - 1; j++) {

            fillcircle(int(0.7071 * controlPoints[i][j][0] - 0.7071 * controlPoints[i][j][1] + 0.5f + 400), int(-0.4082 * controlPoints[i][j][0] - 0.4082 * controlPoints[i][j][1] + 0.8165 * controlPoints[i][j][2] + 0.5f + 300), 3);

        }

    }

    // 绘制贝塞尔曲面

    const int nPoints = 50;  // 每行/列计算的点数

    float uStep = 1.0f / nPoints;

    float vStep = 1.0f / nPoints;

    for (float u = 0; u < 1; u += uStep) {

        for (float v = 0; v < 1; v += vStep) {

            float x = 0, y = 0, z = 0;

            for (int i = 0; i < N; i++) {

                for (int j = 0; j < N; j++) {

                    // 计算贝塞尔基函数的值

                    float basisU = powf(1 - u, N - 1 - i) * powf(u, i) * float(C(N - 1, i));

                    float basisV = powf(1 - v, N - 1 - j) * powf(v, j) * float(C(N - 1, j));

                    float basis = basisU * basisV;

                    // 使用贝塞尔基函数的值和控制点计算曲面上的点

                    x += basis * controlPoints[i][j][0];

                    y += basis * controlPoints[i][j][1];

                    z += basis * controlPoints[i][j][2];

                }

            }

            // 将曲面上的点连接起来

            display(x, y, z);

        }

    }

}

//主函数

int main(){

    initgraph(800, 600);

    Bezier();

    ExMessage m;

    while (1) {

        m = getmessage(EX_MOUSE | EX_KEY);

        switch (m.message) {

        case WM_RBUTTONDOWN:

            //右键修改坐标信息

            closegraph();

            int row, column, newx, newy, newz;

            //输入数组中的坐标，进行修改

            cout << "which point do you want to change? please input its row & column array number" << endl;

            while (1) {

                cin >> row;

                cin >> column;

                if (row >= N) {

                    cout << "row number input error, try again" << endl;

                }

                else if (column >= N) {

                    cout << "column number input error, try again" << endl;

                }

                else {

                    break;

                }

            }

            cout << "please input the reset coordinate" << endl;

            cin >> newx >> newy >> newz;

            controlPoints[row][column][0] = newx;

            controlPoints[row][column][1] = newy;

            controlPoints[row][column][2] = newz;

            cout << "successfully reset, please wait a second to see a new graph" << endl;

            initgraph(800, 600);

        case WM_LBUTTONDOWN:

            //左键绘制

            Bezier();

        case WM_KEYDOWN:

            //退出图形化界面

            if (m.vkcode == VK_ESCAPE) {

                return 0;

            }

        }

    }

   

    _getch();

    closegraph();

    return 0;

}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/570103.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

css3新增特性

css3新增特性

1. 初始化 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevice-width, …
阅读更多...
怎么通过ecs云服务器来给小程序发送消息

怎么通过ecs云服务器来给小程序发送消息

如果您想通过 ECS 云服务器向小程序发送消息&#xff0c;可以使用 WebSocket 技术。具体步骤如下&#xff1a; 1. 在 ECS 云服务器上搭建 WebSocket 服务器。您可以使用 Node.js、Java、Python 等编程语言来实现 WebSocket 服务器&#xff0c;具体实现方式可参考相关技术文档或…
阅读更多...
Java笔记——KMP算法

Java笔记——KMP算法

KMP算法 文章目录 KMP算法KMP算法介绍主要逻辑Next数组KMP搜索代码解释生成next数组模式串匹配 源码展示 KMP算法介绍 KMP算法是一种串的模式匹配算法&#xff0c;用来求子串在主串的位置。是数据结构中比较难的一种算法。KMP算法的核心在于点在于如何利用子串生成next数组&am…
阅读更多...
vim的使用、vim入门的三种常用模式、以及vim中常用的命令(超详细)

vim的使用、vim入门的三种常用模式、以及vim中常用的命令(超详细)

vim 入门的三种常用模式&#xff1a;分别是 1. 命令模式、2. 插入/编辑模式、3. 底行模式 1. 命令模式 控制屏幕光标的移动&#xff0c;字符、字或行的删除&#xff0c;移动复制某区段及进入Insert mode下&#xff0c;或者到 last line mode 如下&#xff0c;这个就是命令模式…
阅读更多...
Numpy入门看这一篇就够了【史上入门最简单，开袋即食】

Numpy入门看这一篇就够了【史上入门最简单，开袋即食】

一边学习一边分享&#xff0c;好记性不如烂笔头 目录 一边学习一边分享&#xff0c;好记性不如烂笔头 NumPy问题思考&#xff1a; numpy是什么&#xff1f; 为什么要学习numpy&#xff1f; numpy是怎么组成的&#xff1f;特点是什么&#xff1f; numpy的应用场景有哪些&a…
阅读更多...
css定位模式

css定位模式

1. 为什么需要定位&#xff1f; <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"…
阅读更多...
自动化专业求职方向与前景分析（合集)

自动化专业求职方向与前景分析（合集)

自动化专业求职方向与前景分析 自动化专业求职方向 自动化专业是近几年高校教育改革中几个控制类专业合并后形成的宽口径专业&#xff0c;其实自动化就是搞控制的&#xff0c;用老师的话说就是控制一切可以控制的物理量&#xff0c;还说学自动化的人都要有控制的欲望。所谓控制…
阅读更多...
Augmented Language Models（增强语言模型）

Augmented Language Models（增强语言模型）

Augmented Language Models: A Survey 先上地址&#xff1a;https://arxiv.org/pdf/2302.07842.pdf 概率论难以支撑通用人工智能技术的诞生。—— Yann LeCun LLMs取得的巨大进展不再多说&#xff0c;它目前被诟病最多的问题是其会提供非事实但看似可信答案&#xff0c;即幻觉…
阅读更多...
数组排序——从荷兰国旗问题到快速排序

数组排序——从荷兰国旗问题到快速排序

本文首先将会介绍荷兰国旗问题&#xff0c;再讲述如何从该问题过渡到快速排序。 荷兰国旗问题 荷兰国旗问题&#xff08;Dutch National Flag Problem&#xff09;是由荷兰计算机科学家Edsger Dijkstra所提出&#xff0c;该问题的描述如下&#xff1a; 给定n个红、白、蓝三种颜…
阅读更多...
JNDI学习笔记

JNDI学习笔记

最近在研究JNDI注入漏洞&#xff0c;就先浅浅的学习以下JNDI相关知识。 JNDI对各种目录服务的实现进行抽象和统一化。 在 Java 应用中除了以常规方式使用名称服务(比如使用 DNS 解析域名)&#xff0c;另一个常见的用法是使用目录服务作为对象存储的系统&#xff0c;即用目录服务…
阅读更多...
SpringBoot --- 基础篇

SpringBoot --- 基础篇

一、快速上手SpringBoot 1.1、概述 SpringBoot开发团队认为原始的Spring程序初始搭建的时候可能有些繁琐&#xff0c;这个过程是可以简化的&#xff0c;那原始的Spring程序初始搭建过程都包含哪些东西了呢&#xff1f;为什么觉得繁琐呢&#xff1f;最基本的Spring程序至少有一…
阅读更多...
大数据：VMware | Ubuntu | Hadoop | Spark | VMwaretools | Python 安装配置总结

大数据：VMware | Ubuntu | Hadoop | Spark | VMwaretools | Python 安装配置总结

一.环境概述 Linux发行版&#xff1a;Ubuntu虚拟机应用&#xff1a;VMware Workstation ProHadoop版本&#xff1a;3.1.3|伪分布式集群JDK版本&#xff1a;JDK1.8.0_162Spark版本:2.4.0Scala版本:2.12.8Python版本:3.6.8 | 3.7.16 二.Ubuntu 2.1 光盘文件 首先进入链接Down…
阅读更多...
因为AI，我被裁了；MJ设计海报全流程；独立开发者每周收入2.3K美元；MJ常用参数超详细介绍 | ShowMeAI日报

因为AI，我被裁了；MJ设计海报全流程；独立开发者每周收入2.3K美元；MJ常用参数超详细介绍 | ShowMeAI日报

&#x1f440;日报&周刊合集 | &#x1f3a1;生产力工具与行业应用大全 | &#x1f9e1; 点赞关注评论拜托啦&#xff01; &#x1f916; 受 AI 影响&#xff0c;这 8 家公司开始裁员…… 为了搞清楚 AI 最近在影响哪些行业、哪些职业&#xff0c;作者花了三天事件找到了八…
阅读更多...
基于SSM的网络在线考试系统

基于SSM的网络在线考试系统

末尾获取源码 开发语言&#xff1a;Java Java开发工具&#xff1a;JDK1.8 后端框架&#xff1a;SSM 前端&#xff1a;Vue 数据库&#xff1a;MySQL5.7和Navicat管理工具结合 服务器&#xff1a;Tomcat8.5 开发软件&#xff1a;IDEA / Eclipse 是否Maven项目&#xff1a;是 前言…
阅读更多...
《Java并发编程实战》课程笔记（二）

《Java并发编程实战》课程笔记（二）

可见性、原子性和有序性问题&#xff1a;并发编程 Bug 的源头 源头之一&#xff1a;缓存导致的可见性问题 在单核时代&#xff0c;所有的线程都是在一颗 CPU 上执行&#xff0c;CPU 缓存与内存的数据一致性容易解决。 因为所有线程都是操作同一个 CPU 的缓存&#xff0c;一个…
阅读更多...
《面试1v1》ThreadLocal

《面试1v1》ThreadLocal

我是 javapub&#xff0c;一名 Markdown 程序员从&#x1f468;‍&#x1f4bb;&#xff0c;八股文种子选手。 面试官&#xff1a; 你好&#xff0c;请问你对 ThreadLocal 有了解吗&#xff1f; 候选人&#xff1a; 您好&#xff0c;我知道 ThreadLocal 是一个 Java 中的类&a…
阅读更多...
【坐标变换】坐标系坐标变换简单推导--未完待续

【坐标变换】坐标系坐标变换简单推导--未完待续

如图所示&#xff0c;假设已知坐标系 ( X , Y ) (X,Y) (X,Y)&#xff0c;旋转后的坐标系为 ( X ′ , Y ′ ) (X,Y) (X′,Y′)&#xff0c;旋转角度为 θ \theta θ&#xff0c;假设点p在 ( X , Y ) (X,Y) (X,Y)坐标系下为 ( x , y ) (x,y) (x,y)&#xff0c;坐标在旋转后的坐标…
阅读更多...
速来！谷歌师兄的LeetCode刷题笔记开源了！

速来！谷歌师兄的LeetCode刷题笔记开源了！

有小伙伴私聊我说刚开始刷LeetCode的时候&#xff0c;感到很吃力&#xff0c;刷题效率很低。我以前刷题的时候也遇到这个问题&#xff0c;直到后来看到这个谷歌师兄总结的刷题笔记&#xff0c;发现LeetCode刷题都是套路呀&#xff0c;掌握这些套路之后&#xff0c;就变得非常简…
阅读更多...
kubernetes高可用+harbor高可用

kubernetes高可用+harbor高可用

kubernetes高可用harbor高可用 基于kubeadm安装kubernetes高可用集群全部主机环境初始化双主节点部署keepalive双主节点初始化kubeadm在k8smaster1节点上初始化k8s在k8smaster2节点上做扩容操作 harbor高可用集群初始化harbor1节点安装环境在另一台节点上配置使用私有harbor仓库…
阅读更多...
初学QT:使用QtDesigner绘制一个简单的界面（Day01）

初学QT:使用QtDesigner绘制一个简单的界面（Day01）

关于Qt 打算在这里记录我学习qt过程中遇见的问题的收获 今天是学习qt的第一天&#xff0c;首先找了一个界面打算照着这个界面写一个一样的 因为是第一天&#xff0c;所以我用的是qt designer写的 其中遇到的问题&#xff1a; 设置背景图片 首先不能直接添加图片到背景图片中…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023