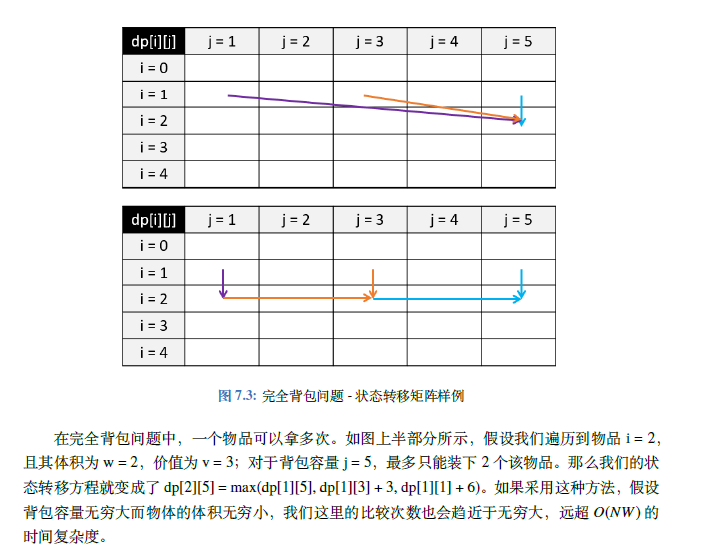
如图所示,假设已知坐标系 ( X , Y ) (X,Y) (X,Y),旋转后的坐标系为 ( X ′ , Y ′ ) (X',Y') (X′,Y′),旋转角度为 θ \theta θ,假设点p在 ( X , Y ) (X,Y) (X,Y)坐标系下为 ( x , y ) (x,y) (x,y),坐标在旋转后的坐标系(即 ( X ′ , Y ′ ) (X',Y') (X′,Y′))中的坐标为 ( l , w ) (l,w) (l,w)。
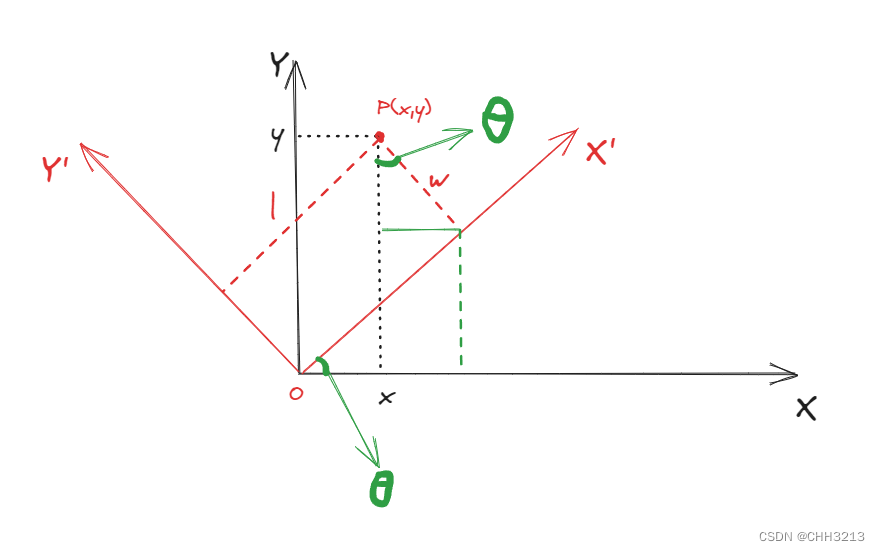
根据图中几何关系,可以表示出
(
x
,
y
)
(x,y)
(x,y)与
(
l
,
w
)
(l,w)
(l,w)的关系。
x
=
l
cos
θ
−
w
sin
θ
y
=
l
sin
θ
+
w
cos
θ
x=l\cos\theta-w\sin\theta\\ y=l\sin\theta+w\cos\theta
x=lcosθ−wsinθy=lsinθ+wcosθ
即坐标转换公式为
[ x y ] = [ cos θ , − sin θ sin θ , cos θ ] [ l w ] \begin{bmatrix} x \\ y \end{bmatrix}=\begin{bmatrix} \cos\theta, \ -\sin\theta \\ \sin\theta, \ \cos\theta \end{bmatrix} \begin{bmatrix} l \\ w \end{bmatrix} [xy]=[cosθ, −sinθsinθ, cosθ][lw]
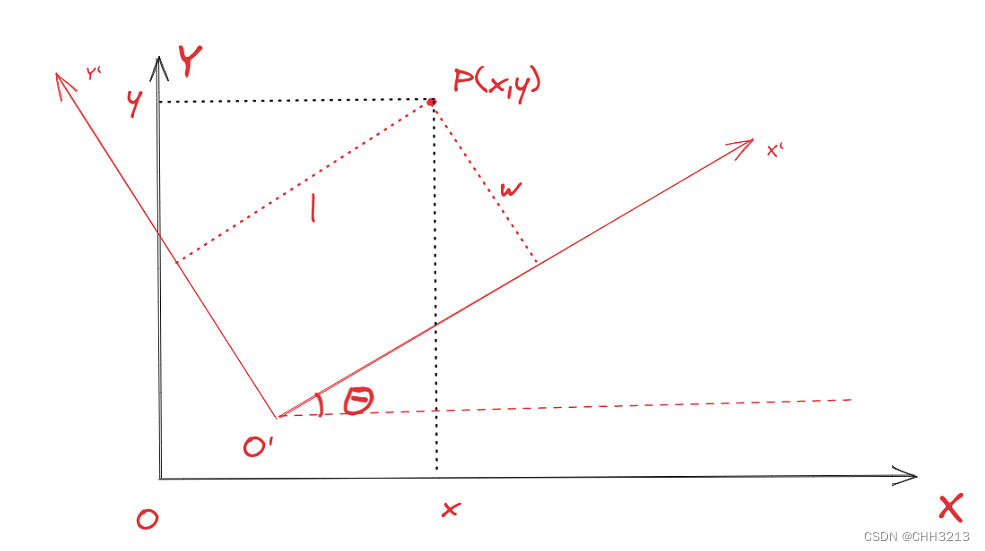
加上平移,如下图所示,假设
(
X
′
,
Y
′
)
(X',Y')
(X′,Y′)原点
O
′
O'
O′在
(
X
,
Y
)
(X,Y)
(X,Y)坐标系下的坐标为
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0),则有以下关系式
[
x
y
]
=
[
cos
θ
,
−
sin
θ
sin
θ
,
cos
θ
]
[
l
w
]
+
[
x
0
y
0
]
\begin{bmatrix} x \\ y \end{bmatrix} =\begin{bmatrix} \cos\theta, \ -\sin\theta \\ \sin\theta, \ \cos\theta \end{bmatrix} \begin{bmatrix} l \\ w \end{bmatrix}+\begin{bmatrix} x_0 \\ y_0 \end{bmatrix}
[xy]=[cosθ, −sinθsinθ, cosθ][lw]+[x0y0]
[ cos θ , − sin θ sin θ , cos θ ] \begin{bmatrix} \cos\theta, \ -\sin\theta \\ \sin\theta, \ \cos\theta \end{bmatrix} [cosθ, −sinθsinθ, cosθ] 其实就是旋转矩阵。
分割线–未完待续