翻译自 Real-Time C++ Efficient Object-Oriented and Template Microcontroller Programming 4th Edition - Kormanyos, Christopher，这书涉及了从C++11 到C++20 的内容，主要介绍使用C++ 的模板、面向对象等特性设计嵌入式程序。书里的示例代码都是公开的：https://github.com/ckormanyos/real-time-cpp

第一篇地址，有原书PDF：https://blog.csdn.net/Etberzin/article/details/130867462

---

三、轻松学习C++ 的一个子集

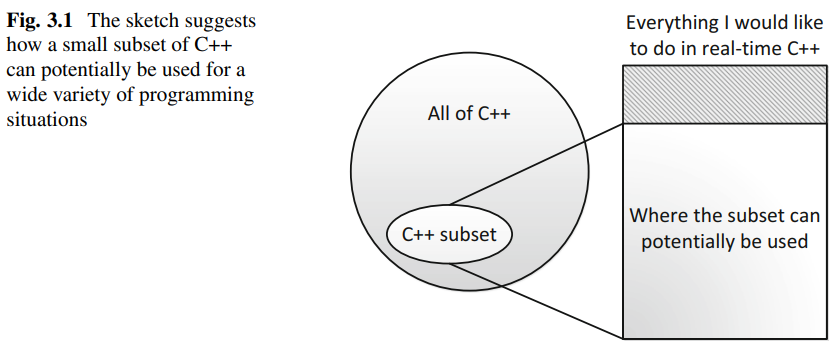
新接触实时C++的开发人员可能希望在花时间掌握C++语言的所有复杂细节之前快速获得一些有用的例子。本章通过提供一个简单而有效的C++ 语言子集来满足这种需求，该子集专门为那些寻求轻量级和可靠的实时C++ 快速入门的人设计。本章中的C++子集代表了一种明智的选择，它包含了一些最容易做到的C++事情，可以在尽可能广泛的编程情况下使用。这个C++子集的定位如图3.1所示。此外，第3.2节还提供了详细的项目，比如使用筛选法计算质数。

3.1 到使用的地方再定义局部变量

在C++ 中，局部变量可以在第一次使用的地方声明，它们不一定需要放在函数的开头。这可以提高代码可读性并促进编译器优化。例如，下面的代码在使用i、j和k前才声明了整型变量。

// chapter03_01-001_declare_locals.cpp
void initialize();
void use_i(const int);
void use_j(const int);
void use_k(const int);

void do_something()
{
	// Initialize someting.
	initialize();
	// Declare i when using it in use_i().
	const int i = 3;
	use_i(i);
	// Declare j when using it in use_j().
	const int j = 7;
	use_j(j);
	// Declare k in the scope of the for-loop.
	for(int k = 0; k < 10; ++k)
	{
		use_k(k);
	}
}

3.2 固定大小的整数类型和质数实例

C++标准库在其<cstdint>头文件中提供了一整套可移植的固定大小整数类型。如第1.8节所述，用户定义的内置整型类型（如my_uint8、my_uint16等）可能会笨拙、难以维护且容易出错，特别是在多个环境中使用时。然而，从C++11 开始，非标准的用户定义类型可以用标准的固定大小整数类型（如std::uint8_t、std::uint16_t、std::uint32_t 等）替换。

例如，下面的代码使用指定宽度的整数变量，如精确16位和至少32位。标准宏UINT8_C()、UINT16_C()、UINT32_C() 以及对应的有符号类型宏也在<cstdint>头文件中定义。

// chapter03_02-001_fixed_size_integer.cpp

#include <cstdint>

// 这个值是固定的16 位
constexpr std::int16_t value16 = INT16_C(0x7FFF);

// 这个值的尺寸至少是32 位
// 4’294’967’295 这个写法中’ 用来任意分隔多位数字，可以按英语习惯，也可以按四位一分，从而提高可读性
constexpr std::uint_least32_t value32 = UINT32_C(4’294’967’295)

正如上面所示，它们可以方便地创建具有指定宽度的数字文字整数值。这些宏也提高了代码的完整性。特别地，它们可能优于常用的后缀，如U、L、UL、LL、ULL等。

考虑如下例子，初始化一个常量10,006,721，这是第664999 个质数：

// chapter03_02-002_prime_number.cpp

#include <cstdint>

// 后缀U 表示unsigned int
constexpr std::uint32_t prime_664999 = 10’006’721U;

这段代码可能不够健壮或存在可移植性问题。整数文字常量10'006'721U表示第664,999个质数。然而，这种表示依赖于后缀U，表示unsigned int。当将这段代码移植到其他平台时，特别是8 位平台，unsigned int 可能不是32 位宽。它可能只有16 位宽，甚至只有8 位宽。在这种情况下，unsigned int不足以容纳整数值10,006,721，初始化可能会产生潜在的混淆（甚至不正确）。

现在我们将稍微修改prime_664999的初始化，以提高编码完整性。在这种情况下，初始化是明确的、清晰表达的和可移植的：

// chapter03_02-002_prime_number.cpp

#include <cstdint>

// Initialize the 664,999th prime number.
// UINT32_C() 等宏有更强的可移植性性
constexpr std::uint32_t prime_664999 = UINT32_C(10’006’721);

宏UINT32_C() 保证能够处理无符号32 位整数数据类型的范围，从0 到4,294,967,295。实际上，保持一致使用固定大小的整数类型并不会对功能产生很大贡献，而是一种风格。这通常会让代码在不同平台上获得相似的表现和运行结果，从而提高可移植性。

在一个中等大小的程序的背景下使用固定大小的整数类型在示例chapter03_02 的代码中展示。在这个例子中，使用埃拉托色尼筛法在8位目标微控制器上计算顺序质数。

示例chapter03_02 使用了本书后面描述的几个C++特性。其中包括模板编程（第5章）、在微控制器环境中使用STL（第5.8节）、硬件驱动程序（第9章）、自定义内存管理（如环形分配器，第10.5节）、多任务（第11章）、浮点计算（第12章）等。这个例子在本书的这个早期阶段提供，是为了提供一个完整且内容丰富的示例。

示例chapter03_02 的理论背景始于数学特殊函数，特别是对数积分函数，即：

$$Li(x)=li(x)-li(2)={\int }_2^x\frac{dt}{log(t)}\text{\hspace{1em}(3.1)}$$

这里li(x)被称为对数积分函数，Li(x)是偏移对数积分函数。

可以从质数计数函数π(x)在质数定理中获得给定上限以下质数数量的估计。这个非凡且著名的定理通过渐近极限将偏移对数积分函数Li(x)与质数计数函数联系起来：

$$\pi (x)\sim Li(x)\text{\hspace{1em}(3.2)}$$

注：师傅，你是干啥的

再次考虑上面的例子：第66499 个质数10,006,721，对于这个素数，式3.1 和式3.2 的结果是：

$$\begin{array}{rl}\frac{10,006,721}{66499}& \approx \frac{\mathrm{665335.4...}-\mathrm{1.045...}}{66499}\\ & \approx \mathrm{1.000504...}\\ & \underset{˜}{?}1\end{array}\text{\hspace{1em}(3.3)}$$

其中，$li(2)\approx 1.045\dots$。在x = 10,006,721 这个特定的数值点上，式3.2 中的比值为1.000504 …，略大于1。这个比值随着x的增加而更接近1，推测在无限大的x时达到1。

在示例chapter03_02 中，目的是计算至少100个质数。为了确定和验证筛选计算的适当限制，我们考虑对数积分函数在x 较大时的一个初级发散渐近级数展开：

$$li(x)\sim \frac{x}{\log x}\sum _{k=0}^{\infty }\frac{k!}{(\log x{)}^k}\text{\hspace{1em}(3.4)}$$

得出渐近数值近似：

$$\pi (x)\sim \left(\frac{x}{\log x}\sum _{k=0}^{\infty }\frac{k!}{(\log x{)}^k}\right)-li(2)\text{\hspace{1em}(3.5)}$$

其中$x$ 足够大。在软件中实现这个计算时，展开式中的循环应该在求和项达到最小值后终止，此后该点开始增加，因为该级数是发散的。

预先知道第100 个质数是541，讲542 代入式3.5，结果是：

$$\begin{array}{rl}\pi (542)& \sim \left(\frac{542}{\log 542}\sum _{k=0}^7\frac{k!}{(\log 542{)}^k}\right)-\mathrm{1.045...}\\ & \approx 108\end{array}\text{\hspace{1em}(3.6)}$$

其中，发散级数从0 到7 展开。这证实了通过将筛选循环的上限设置为 542 的平方根的向下取整值，可以轻松计算前一百个质数。

使用无符号整数值组成的专用容器来保存筛子，每个整数被分成位段。该容器被实现为一个名为dynamic_bitset的模板类。容器中的内存存储使用第 10.5 节中的专用环形分配器。

下面的代码序列显示了模板子程序 compute_primes_via_sieve 的一部分。它直接取自示例 chapter03_02。

template<const std::size_t maximum_value, typename forward_iterator_type, typename alloc>
void compute_primes_via_sieve
(
	forward_iterator_type first)
	{
	// Use a sieve algorithm to generate
	// a table of primes.
	// ...
	// ...
	// Create the sieve of primes.
	// ...
	// ...
	for(local_value_type i = 2U; i < local_value_type(imax);	++i)
	{
			if(sieve.test(i) == false)
			{
				const local_value_type i2 = i * i;
				for(local_value_type j = i2; j < maximum_value;	j += i)
				{
					sieve.set(j);
				}
			}
	}
// ...
// ...
// Fill the prime numbers into the data table
// by extracting them from the sieve of primes.
// ...
// ...
}

注：不知道作者想用这坨鬼东西表达什么，关键的东西全都省略掉，让初学者轻松学习的细节在tm 的哪里

这段代码显示了筛选计算的内部循环。当在筛子中计算上限为 n 的质数时，嵌套循环的计算复杂度大致为$O(n\log \log n)$。有关算法计算复杂度的进一步讨论，请参见第 6.3 节。

筛选计算被初始化并从头到尾完全运行。这是在 app::prime 任务中以约 20 Hz 的频率（即每 50 毫秒左右一次）循环完成的。通过确保计算出的第 100 个质数的值与预期值 541 相符来进行数值验证。

时间测量使用数字示波器，采用第 9.6 节中的方法。在这个特定的例子中，在筛选计算开始和结束时切换 portd.3。每次执行筛选计算的测量运行时间约为 4.3 毫秒，目标硬件为 8 位微控制器。

对质数的研究可以引导人们进入纯数学和应用数学、数论、高性能计算等众多不同领域的迷人主题。有关质数计数函数的更多信息，请参见 [12] 及其中的参考文献。关于计算质数的全面介绍可以在包括 [1] 和 [7] 第二卷等著作中找到。

本书后面，第 16.8 节中的示例 chapter16_08 使用随机选择的 128 位整数来探索质数定理。

注：以下列举的C++ 特性懒得从书里全部搬过来，有个标题当搜索关键词就行了，详细的自己去了解

3.3 bool 类型

3.4 用命名空间组织代码

3.5 基本的类

3.6 基本的模板

3.7 用nullptr 替换NULL

3.8 constexpr 和广义常量表达式

3.9 static_assert

3.10 使用<limits> 头文件

3.11 std::array

3.12 基本的STL 算法

3.13 <numeric> 头文件

3.14 原子操作 atomic_load() 和atomic_store()

3.15 数字分割符

3.16 二进制字面量

从C++14 开始终于引入了二进制字面量，代码中可以用0b 、0B、b 或B 前缀直接写出二进制整数：

// chapter03_16-001_binary_literals.cpp

constexpr std::uint8_t one = UINT8_C(0b1);
constexpr std::uint8_t seven = UINT8_C(0b0000’0111);

3.17 用户自定义字面量

3.18 使用alignof 和alignas

3.19 final 标识符

3.20 用using 替换typedef

3.21 用<span> 实现范围操作

3.22 用<random> 生成随机数

---

注：显然，这书就是一坨垃圾，只能感觉到这作者估计不是工科出身的，他所谓的“practical” 和我们一般人的理解有点不一样，他的“real-time” 大概也不是大伙一般概念中的那个东西。这书能出到第四版，肯定是作者退休了烧钱玩的