目录

3.2.1 二叉树的定义及性质

定义:

二叉树五种基本形态：

特殊二叉树

二叉树的几个重要性质

二叉树的抽象数据类型定义

操作集：

常用遍历：

3.2.2 二叉树的存储结构

顺序存储结构

数组实现

链表实现

---

3.2.1 二叉树的定义及性质

定义:

二叉树T：一个有穷的结点集合。

• 这个集合可以为空(称为空二叉树)。
• 若不为空，则它是由根结点和称为其左子树TL和右子树TR的 两个不相交的二叉树组成。、
• 可以视作是度为2的树，但有左右子树之分

二叉树五种基本形态：

1. 空树
2. 只有一个根结点
3. 有一个根结点，根结点有左子树（右子树为空）
4. 有一个根结点，根结点有右子树
5. 有一个根结点，根结点有左右子树

特殊二叉树

二叉树的几个重要性质

二叉树第i层的最大结点数为：2^i-1(i>=1)

深度为k的二叉树有最大结点总数为：(2^k) - 1(k>=1) 最大时称为满二叉树

二叉树结点可以分为三种类型：

• 叶结点：没有子结点的个数，称为n0
• 只有一个子结点的个数，称为n1
• 有两个子结点的个数，称为n2

则n0=n2+1

证明：用边的数量来证明，总边数=n0+n1+n2-1，n0对向下的边没有贡献，前面的等式可以写成n0*0+n1*1+n2*2 = n0+n1+n2-1，整理即可得到待证式子

二叉树的抽象数据类型定义

类型名称：二叉树

数据对象集：一个有穷的结点集合

数据对象集若不为空，则由根结点和其左右二叉子树组成

操作集：

BT∈BinTree,item∈ElementType,重要操作：

Boolean IsEmpty(BinTree BT)：判断BT是否为空

void Traversal(BinTree BT):遍历，按某顺序访问每个结点

BinTree CreateBinTree():创建一个二叉树

常用遍历：

先序遍历（根->左子树->右子树）voidPreOrderTraversal(BinTree BT);

中序遍历（左子树->根->右子树）voidInOrderTraversal(BinTree BT);

后序遍历（左子树->右子树->根）voidPostOrderTraversal(BinTree BT);

层次遍历（从上到下，从左到右）void LevelOrderTraversal(BinTree BT);

3.2.2 二叉树的存储结构

顺序存储结构

数组实现

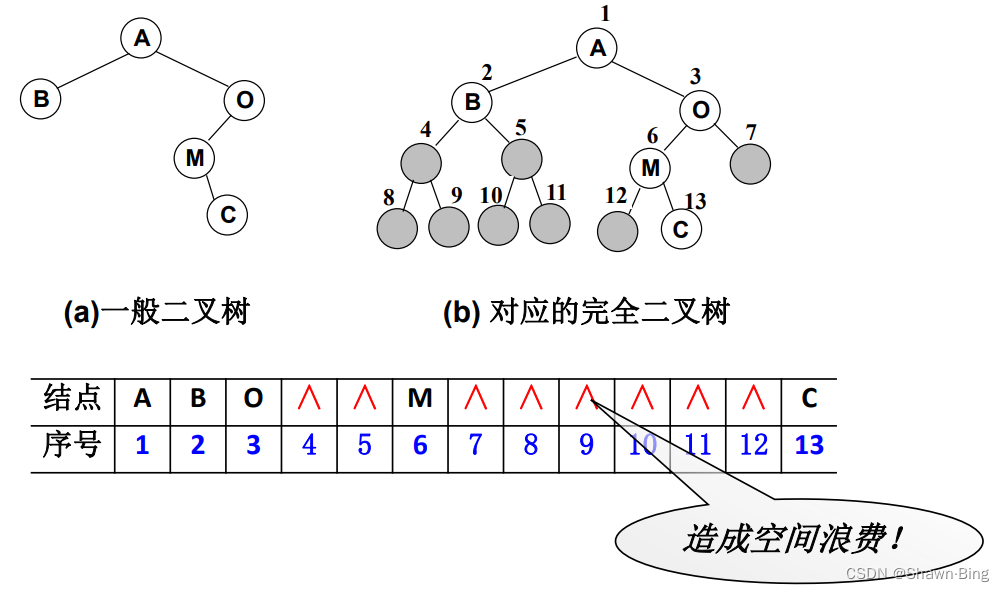
首先我们想到用数组实现，而之前提到的完全二叉树就非常契合，我们可以按从上到下，从左往右的顺序存储N个结点的完全二叉树的结点父子关系

 一般二叉树也可采用这种结构，即在没有数据的位置留空数据，但仍然会浪费空间

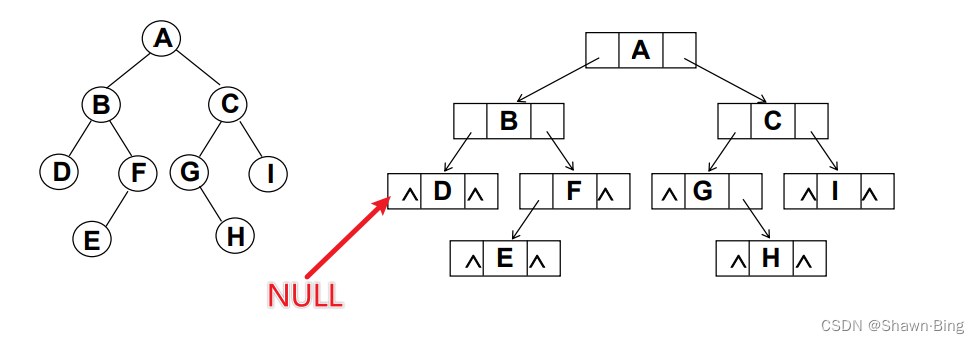
链表实现

一般二叉树在前面已经提到，可以使用一个结点包含三个域，一个存储数据信息，一个指向左子树，一个指向右子树

typedef struct TreeNode *BinTree;
typedef BinTree Position;
struct TreeNode{
    ElementType Data;
    BinTree Left;
    BinTree Right;
}