CSDN周赛55期 - 简单分析

news2024/10/7 12:23:44

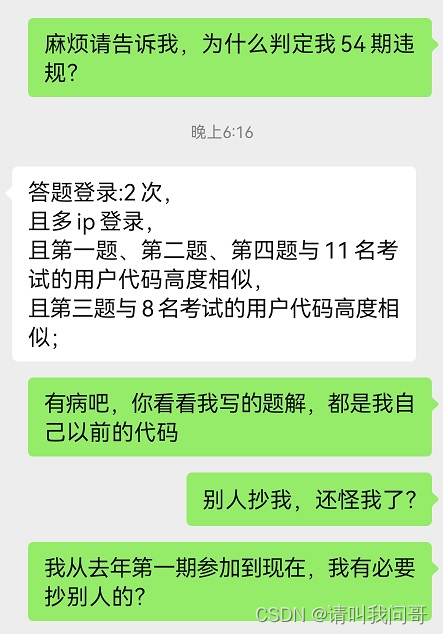
上期周赛被判抄袭了。。。无语。我从第一期周赛一步步走来，所有题我都做过，我还需要抄袭？

虽然第一时间去申诉，但貌似并没什么用。算了，C站的审核也就这样了，失望+寒心。

本期还是《计算之魂》主题赛——不得不说，该系列比赛的编程题质量都还不错。本期两道编程题，至少对我来说，还是挺难的。

前面选择题就不说了，本期问哥特意花了点时间翻书——我就不信找不到答案了。

填空题再次出现，一个月后围观打脸。

题目描述：从1开始，每次增加1、2或3，有（）种方法可以加到9。

但是，C站还是延续了填空题必出妖的传统，标准答案给的 44，明显错了。如果大家能够读懂题意的话，本题其实就是上台阶（斐波那契数列）的进阶版。“加到”某个数，可以理解为到达某层台阶 n，而到达的上一步可以是 3 步（n - 3）之前、2步（n - 2）之前、1步（n - 1）之前。这三个地方都可以 1 步到达台阶 n。于是可以把问题转化为到达这三个地方的递归求解，最后将所有方案汇总，于是可列递归代码如下：

def fun(n):
    if n == 1: return 1
    if n < 1: return 0
    return fun(n-3)+fun(n-2)+fun(n-1)

我注意到讨论群中有人在争论 fun(1) 应该等于 0，理由是题目是“从1开始”，所以“加到”1的方法数是0。我只想说，这里的 return 1 和 return 0 其实可以理解为该位置可达与否，最终得到的结果是可达的计数 —— 当然在python里，由于数据的弱类型，换成 return True 和 return False，该代码可以直接运行。

再怀疑的话，穷举出来就可以证明了吧。使用深搜算法穷举所有方案如下：

编程题。两题都很有挑战性。

第一题、取石子

将n堆石子摆成一排，游戏规则是：两人轮流从最左或最右的一堆中取出若干颗石子（可以将一堆整个取掉但不能不取），无法再取者判负。问题是：对于给定的初始石子局面，是否存在先手必胜策略？

虽然看得出来是区间DP，但转移方程的思维难度不小。本题也是上古原题：[ZJOI2009]取石子游戏 - 洛谷

大家可以自行查阅题解——虽然未必能一下子搞懂。

由于本题只有两个答案，非“Yes”即“No”。而周赛的用例，直接 print(“Yes”) 即可通过70%，于是问哥果断选择骗分通过。等以后有空，再仔细研究研究。

第二题、勾股定理困难版

给定斜边z的值，求所有直角边x和y的组合数（x、y和z都是正整数）。

官方给的题解如下图：

反正我是没看懂，数学好的同学可以解析一下再出份详细题解。

在这里问哥简要说一下自己野路子的思路：

由于 z 很大很大（后面的 0 数不清），所以穷举 $O(z)$ 必定超时，无法通过，只能从寻找勾股数的规律入手。

结合经验并简单查阅资料就可以发现（前面都翻书了，还有什么不能查资料的？），一组勾股数（x、y、z）具有如下规律：

斜边 z 为偶数时，该组勾股数必然全是偶数——不存在互质；
斜边 z 为奇数时，该组勾股数的 x 和 y 必然一个是奇数、一个是偶数。

当 z 为偶数时，所有满足条件的勾股数组合，一定都可以约分成互质的勾股数。比如当 $z=50$ ，满足条件的组合有（30,40,50）、（14,48,50），可以分别约分成为互质的（3,4,5）、（7,24,25）。于是，我们要找斜边为 z 的勾股数组合，等价于寻找所有互质的勾股数组合——这些组合中的斜边都是 z 的奇因数。所以我们只要分析，当 z 的奇数因子（偶数不存在互质的勾股数）分别作为新的斜边时，各存在多少互质的勾股数组合（也可能一个都没有），再将这些组合数累加在一起即可。