【数组】

为什么Go语言的切片是成倍扩容？

【链表】

单链表

循环链表

双向链表

双向循环链表

数组和链表如何选择？

如何使用链表实现 LRU 缓存淘汰算法？

链表的一些操作

【每日一练】

【数组】

数组（Array）是一种线性表数据结构，使用一组连续的内存空间来存储相同类型的数据；数组需要一块连续的内存空间来存储，对内存的要求比较高。数组支持随机访问，根据下标（索引）随机访问的时间复杂度为 O(1)。但是插入和删除操作就比较麻烦了，因为在数组中某个位置插入一个新元素，需要对已有位置之后的元素全部往后挪一位；删除的时候需要往前挪一位，因为要保证连续性。

【访问数组元素】存储数组时会事先分配一段连续的内存空间，将数组元素依次存入内存。因为数组元素的类型都是一样的，所以每个元素占用的空间大小也是一样的，这样就很容易用 “数组的开始地址 + index * 元素大小” 的计算方式快速定位到指定索引位置的元素，因此数组基于下标随机访问的时间复杂度是 O(1)。
【数组插入元素】若对一个数组 int[n] 的第k个位置插入数据，需要在 k到n 的位置往后移动，如果k在最后一位，那么就是最好情况时间复杂度 O(1)；如果k在第一位，那么就是最坏情况复杂度为O(n)，因此平均复杂度为O(n)。如果数组中的数据不是有序的（也就是无规律的情况下），可以直接把第 k 个位置上的数据移到最后，然后将插入的数据直接放在第k个位置上，这样时间复杂度就降为 O(1) 了。
【数组删除元素】与插入类似，为了保持内存的连续性，最好情况时间复杂度 O(1)，最坏情况复杂度为O(n)，平均复杂度为O(n)。为了提高效率，可以在删除的时候不真实删除，而是做一个标记，当发现没有更多空间存储时，再将标记好的多次删除业务执行真正的删除操作。

【问】为什么数组的下标从0开始？
【答】因为获取数组元素的方式是按照以下的公式获取的：base_address + index * data_size，其中index是索引，data_size是数据类型大小。如果数组的下标从1开始，那么获取数组 array[index] 的内存地址就成了 base_address + (index - 1) * data_size，每次随机访问数组元素都多了一次减法运算，对于 CPU 来说就是多了一次减法指令。当然数组下标从0开始也有一定的历史原因。

静态数组：需要事先指定空间大小，并且当使用者分配完内存之后，数组空间就不再能扩展了，也就是大小无法改变，唯一的解决方案只能是重新申请一个更大的数组，如果自己手动实现这个过程会很麻烦；
动态数组：把静态数组扩容的实现方式封装起来，使用者直接拿来用就可以了。Go语言中的切片和 Java 中的 ArrayList 就是动态数组。

为什么Go语言的切片是成倍扩容？

Go语言的切片是一个引用类型的容器，底层指向的是一个数组，切片是对数组的连续片段引用。关于Go语言切片的用法可以参考：Go语言中array、slice、map的用法和细节分析_浮尘笔记的博客-CSDN博客

当向切片中添加数据时，如果没有超过容量则直接添加，如果超过容量了则会自动扩容(成倍增长)，比如下面的代码：

// go-algo-demo/algo01/demo2.go
func appendSlice() {
	sli := []int{1, 2, 3}
	fmt.Printf("slice=%v len=%d cap=%d\n", sli, len(sli), cap(sli)) //slice=[1 2 3] len=3 cap=3
	sli = append(sli, 4)
	fmt.Printf("slice=%v len=%d cap=%d\n", sli, len(sli), cap(sli)) //slice=[1 2 3 4] len=4 cap=6
	sli = append(sli, 5)
	fmt.Printf("slice=%v len=%d cap=%d\n", sli, len(sli), cap(sli)) //slice=[1 2 3 4 5] len=5 cap=6
	sli = append(sli, 6)
	fmt.Printf("slice=%v len=%d cap=%d\n", sli, len(sli), cap(sli)) //slice=[1 2 3 4 5 6] len=6 cap=6
	sli = append(sli, 7)
	fmt.Printf("slice=%v len=%d cap=%d\n", sli, len(sli), cap(sli)) //slice=[1 2 3 4 5 6 7] len=7 cap=12
}

func main() {
	appendSlice()
}

上面示例中一开始定义了长度为3、容量为3的切片，当扩容到4的时候，切片的容量就在原有3的基础上翻了一倍，变成了6，同样的在容量达到6的时候继续扩容又翻了一倍，变成了12。为什么要这么设计呢？

假设每次扩容都只是扩大一个元素的容量，那么每次给切片中插入新元素都会触发扩容操作，而每次扩容都会进行所有元素的复制操作。所以如果要插入 n 个元素，需要拷贝的次数为：1 + 2 + 3 + … + n = n^2，复杂度是O(n^2)，均摊下来每次操作时间复杂度就是 O(n)
假设每次不是扩展一个容量，而是扩展 K 个容量，那么每插入 K 次数据就需要进行一次扩展操作，每次扩展仍然需要复制全部元素，所以总的拷贝次数是：K + 2K + 3K + … + floor(n/K) = n^2，复杂度同样是O(n^2)，均摊下来每次操作时间复杂度还是 O(n)
如果是二倍扩容，假设一共还是插入 K 次数据，总的拷贝次数是：1 + 2 + 4 + 8 + … + 2^x = 2^(x+1) − 1，其中 x 是 logn 向上取整（因为容量每次都在翻番），因此插入 n 个元素的复杂度是O(n)，均摊到每次插入的扩容复杂度就为O(1)

【链表】

链表相比于数组，不需要连续的内存空间，它只需要通过 “指针” 将一组零散的内存块数据串联起来就可以了。假设需要存储20MB的数据，如果此时内存中有20MB的空间，但这些空间不是连续的，那么就不能存储数组，但却可以存储链表。链表也支持数据的查找、插入和删除操作。链表一般分为单链表、双向链表、循环链表、双向循环链表。

单链表

拥有一个数据节点和向后的指针，就是单链表。单链表的头结点用来记录链表的基地址，尾结点的指针指向一个空地址 NULL。

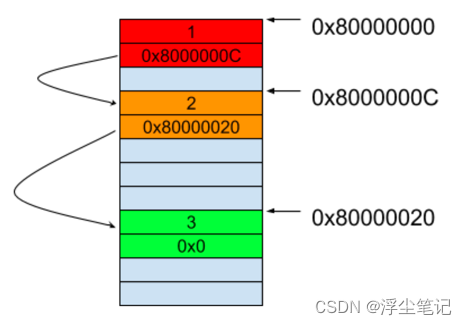
链表的存储空间不是连续的，因此在链表中插入或者删除一个数据并不需要搬移结点，直接把新元素的指针指向原来的目标位置就可以了，如下图所示：

如果要查找链表中的一个元素，无法使用一个固定的公式来直接算出要查找的元素的地址，必须要从第一个元素开始一个一个地遍历N次才能找到第N个元素。因此，在链表中插入和删除数据的时间复杂度是O(1)，但是链表中查找数据的时间复杂度是O(n)，刚好和数组相反。

把链表想象成很多人在排队，队伍中的每个人都只知道自己后面的人是谁，如果想知道排在某个位置的人是谁，就需要从第一个人开始一个一个往下数。所以链表随机访问的时间复杂度就是O(n)。

虽然链表在新增和删除数据上有优势，但这个优势并不实用，因为在新增数据时，通常需要先查找到指定的元素所对应的位置，再新增元素。

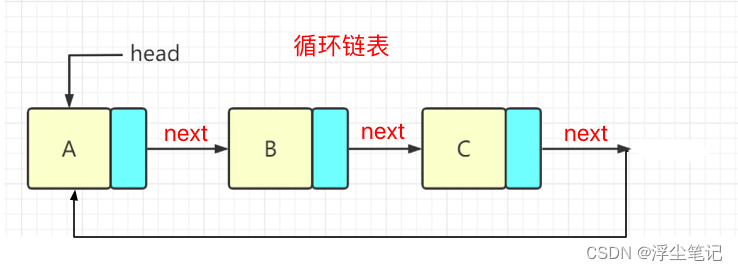
循环链表

循环链表就是把单链表的首尾节点连接起来，优点是从链尾到链头比较方便，当要处理的数据具有环型结构特点时就适合采用循环链表，比如约瑟夫问题。

双向链表

拥有一个数据节点和向前、向后的指针，就是双向链表，支持两个方向，每个结点有一个指针指向后面的结点（后继节点），还有一个指针指向前面的结点（前驱结点）。双向链表需要额外的两个空间来存储后继结点和前驱结点的地址，所以存储同样多的数据，双向链表要比单链表占用更多的内存空间，但是却可以在O(1)时间复杂度的情况下查找前驱结点，相当于又是一种“空间换时间”的逻辑。

还是用上面排队的例子来说，双向链表就相当于队伍中的每个人知道自己后面和前面的人是谁。

对于执行较慢的程序，可以通过消耗更多的内存（空间换时间）来进行优化；而对于消耗过多内存的程序，可以通过消耗更多的时间（时间换空间）来降低内存的消耗。具体问题具体对待。

下面使用Go语言实现了一个双向链表：

// go-algo-demo/algo01/double_list.go
package main

import "fmt"

type ListNode struct {
	Value int
	Prev  *ListNode
	Next  *ListNode
}

type DoubleList struct {
	Head   *ListNode
	Tail   *ListNode
	Length int
}

// 给链表中追加元素
func (list *DoubleList) Append(x int) {
	node := &ListNode{Value: x}
	tail := list.Tail
	if tail == nil {
		list.Head = node
		list.Tail = node
	} else {
		tail.Next = node
		node.Prev = tail
		list.Tail = node
	}
	list.Length += 1
}

// 获取链表中的元素
func (list *DoubleList) Get(idx int) *ListNode {
	if list.Length <= idx {
		return nil
	}
	curr := list.Head
	for i := 0; i < idx; i++ {
		curr = curr.Next
	}
	return curr
}

// 在链表中指定元素后面插入新元素
func (list *DoubleList) InsertAfter(x int, prevNode *ListNode) {
	node := &ListNode{Value: x}
	if prevNode.Next == nil {
		prevNode.Next = node
		node.Prev = prevNode
	} else {
		nextNode := prevNode.Next
		nextNode.Prev = node
		node.Next = nextNode
		prevNode.Next = node
		node.Prev = prevNode
	}
}

// 遍历输出链表的元素
func (list *DoubleList) foreach() {
	curr := list.Head
	for curr != nil {
		fmt.Printf("%d ", curr.Value)
		curr = curr.Next
	}
	fmt.Println()
}

func main() {
	list := new(DoubleList)
	list.Append(1)
	list.Append(2)
	list.Append(3)
	list.Append(4)
	list.Append(5)
	list.foreach() //1 2 3 4 5

	node := list.Get(3)     //获取第3个元素的位置信息(从0开始)
	fmt.Println(node.Value) //4

	list.InsertAfter(9, node) //在第3个位置插入一个新元素9
	list.foreach()            //1 2 3 4 9 5
}

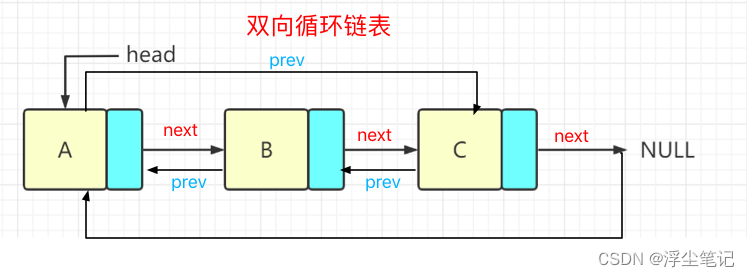
双向循环链表

就是把双向链表的收尾连接起来。

用来检查链表代码是否正确的边界条件：

如果链表为空时，代码是否能正常工作？
如果链表只包含一个结点时，代码是否能正常工作？
如果链表只包含两个结点时，代码是否能正常工作？
代码逻辑在处理头结点和尾结点的时候，是否能正常工作？

数组和链表如何选择？

并不能简单地说链表和数组哪个更好，而是要根据使用的场景做出合适的选择。如果某段代码对内存的使用的要求很高，那么应该优先选择数组，因为链表中的每个结点都需要消耗额外的存储空间去存储一份指向下一个结点的指针，所以内存消耗会翻倍。而且对链表频繁的插入和删除操作还会导致频繁的内存申请和释放，容易造成内存碎片，程序就有可能会频繁的进行垃圾回收操作。

链表更适用于删除、插入、遍历操作频繁的场景，而不适用于随机访问索引频繁的场景。比如在内存池、操作系统进程管理、最常用的缓存淘汰算法 LRU 中都有应用。
如果数据元素大小确定，删除插入的操作并不多，那么数组可能更适合些。

时间复杂度	数组	链表
插入和删除	O(n)	O(1)
随机访问	O(1)	O(n)

如何使用链表实现 LRU 缓存淘汰算法？

常见的缓存有：CPU 缓存、数据库缓存、浏览器缓存等等。当缓存被用满时，需要使用缓存淘汰策略来决定哪些数据被清理出去，常见的策略有三种：

先进先出策略 FIFO（First In，First Out）
最少使用策略 LFU（Least Frequently Used）
最近最少使用策略 LRU（Least Recently Used）。

使用链表来实现一个LRU算法的思路如下（点这里查看代码）：

维护一个有序单链表，越靠近链表尾部的结点是越早之前访问的，当有一个新的数据被访问时，从链表头开始顺序遍历链表。
如果此数据之前已经被缓存在链表中了，那么遍历得到这个数据对应的结点并将其从原来的位置删除，然后再插入到链表的头部。
如果此数据没有在缓存链表中，判断如果此时缓存未满，则将此结点直接插入到链表的头部；如果此时缓存已满，则链表尾结点删除，将新的数据结点插入链表的头部。
不管缓存有没有满，都需要遍历一遍链表，所以这种基于链表实现LRU的思路，它的缓存访问的时间复杂度为 O(n)。

链表的一些操作

链表可以有下面这些操作：单链表反转、判断单链表是否有环、两个有序单链表合并、删除倒数第N个节点、获取中间节点等，参考代码如下：

// go-algo-demo/algo01/list_demo.go
package main

import (
	"fmt"
)

// 单链表节点
type ListNode struct {
	next  *ListNode
	value interface{}
}

// 单链表
type LinkedList struct {
	head *ListNode
}

// 打印链表
func (this *LinkedList) Print() {
	cur := this.head.next
	format := ""
	for nil != cur {
		format += fmt.Sprintf("%+v", cur.value)
		cur = cur.next
		if nil != cur {
			format += "->"
		}
	}
	fmt.Println(format)
}

/*
单链表反转
时间复杂度：O(N)
*/
func (this *LinkedList) Reverse() {
	if nil == this.head || nil == this.head.next || nil == this.head.next.next {
		return
	}

	var pre *ListNode = nil
	cur := this.head.next
	for nil != cur {
		tmp := cur.next
		cur.next = pre
		pre = cur
		cur = tmp
	}

	this.head.next = pre
}

/*
判断单链表是否有环
*/
func (this *LinkedList) HasCycle() bool {
	if nil != this.head {
		slow := this.head
		fast := this.head
		for nil != fast && nil != fast.next {
			slow = slow.next
			fast = fast.next.next
			if slow == fast {
				return true
			}
		}
	}
	return false
}

/*
两个有序单链表合并
*/
func MergeSortedList(l1, l2 *LinkedList) *LinkedList {
	if nil == l1 || nil == l1.head || nil == l1.head.next {
		return l2
	}
	if nil == l2 || nil == l2.head || nil == l2.head.next {
		return l1
	}

	l := &LinkedList{head: &ListNode{}}
	cur := l.head
	curl1 := l1.head.next
	curl2 := l2.head.next
	for nil != curl1 && nil != curl2 {
		if curl1.value.(int) > curl2.value.(int) {
			cur.next = curl2
			curl2 = curl2.next
		} else {
			cur.next = curl1
			curl1 = curl1.next
		}
		cur = cur.next
	}

	if nil != curl1 {
		cur.next = curl1
	} else if nil != curl2 {
		cur.next = curl2
	}

	return l
}

/*
删除倒数第N个节点
*/
func (this *LinkedList) DeleteBottomN(n int) {
	if n <= 0 || nil == this.head || nil == this.head.next {
		return
	}

	fast := this.head
	for i := 1; i <= n && fast != nil; i++ {
		fast = fast.next
	}

	if nil == fast {
		return
	}

	slow := this.head
	for nil != fast.next {
		slow = slow.next
		fast = fast.next
	}
	slow.next = slow.next.next
}

/*
获取中间节点
*/
func (this *LinkedList) FindMiddleNode() *ListNode {
	if nil == this.head || nil == this.head.next {
		return nil
	}
	if nil == this.head.next.next {
		return this.head.next
	}

	slow, fast := this.head, this.head
	for nil != fast && nil != fast.next {
		slow = slow.next
		fast = fast.next.next
	}
	return slow
}

// 测试
var l *LinkedList

func init() {
	n5 := &ListNode{value: 5}
	n4 := &ListNode{value: 4, next: n5}
	n3 := &ListNode{value: 3, next: n4}
	n2 := &ListNode{value: 2, next: n3}
	n1 := &ListNode{value: 1, next: n2}
	l = &LinkedList{head: &ListNode{next: n1}}
}

// 测试:单链表反转
func reverse() {
	l.Print() //1->2->3->4->5
	l.Reverse()
	l.Print() //5->4->3->2->1
}

// 测试:判断单链表是否有环
func hasCycle() {
	fmt.Println(l.HasCycle())                                    //false
	l.head.next.next.next.next.next.next = l.head.next.next.next //加环
	fmt.Println(l.HasCycle())                                    //true
}

// 测试:两个有序单链表合并
func mergeSortedList() {
	n5 := &ListNode{value: 9}
	n4 := &ListNode{value: 7, next: n5}
	n3 := &ListNode{value: 5, next: n4}
	n2 := &ListNode{value: 3, next: n3}
	n1 := &ListNode{value: 1, next: n2}
	l1 := &LinkedList{head: &ListNode{next: n1}}

	n10 := &ListNode{value: 10}
	n9 := &ListNode{value: 8, next: n10}
	n8 := &ListNode{value: 6, next: n9}
	n7 := &ListNode{value: 4, next: n8}
	n6 := &ListNode{value: 2, next: n7}
	l2 := &LinkedList{head: &ListNode{next: n6}}

	MergeSortedList(l1, l2).Print() //1->2->3->4->5->6->7->8->9->10
}

// 测试:删除倒数第N个节点
func deleteBottomN() {
	l.Print()          //1->2->3->4->5
	l.DeleteBottomN(3) //删除倒数第3个节点
	l.Print()          //1->2->4->5
}

// 测试:获取中间节点
func findMiddleNode() {
	l.DeleteBottomN(1)              //删除倒数第1个节点
	l.DeleteBottomN(1)              //再次删除倒数第1个节点
	l.Print()                       //1->2->3
	fmt.Println(l.FindMiddleNode()) //&{0xc000010078 2}
}

func main() {
	//reverse()
	//hasCycle()
	//mergeSortedList()
	//deleteBottomN()
	findMiddleNode()
}

【每日一练】

力扣9. 回文数

给你一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false 。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

例如，121 是回文，而 123 不是。

示例 1：输入：x = 121，输出：true

思路 1：判断 x 是否为负数，如果是负数直接返回；反转 x , 如果反转之后的值与原来的值不同直接返回 false；如果不为负数，同时与反转后的值相等则返回 true。时间复杂度: O(N)，空间复杂度: O(N)

// go-algo-demo/algo01/demo2.go
func isPalindrome1(x int) bool {
	if x < 0 { // 排除小于0的数
		return false
	}
	xStr := strconv.Itoa(x)
	xStrReverse := make([]rune, 0)
	for i, _ := range xStr {
		xStrReverse = append(xStrReverse, rune(xStr[len(xStr)-1-i]))
	}
	for i := 0; i < len(xStr); i += 1 { // 通过字符串进行反转，对比数字是否相等就行
		if rune(xStr[i]) != xStrReverse[i] {
			return false
		}
	}
	return true
}

func main() {
	fmt.Println(isPalindrome1(12321)) //true
	fmt.Println(isPalindrome1(1212))  //false
}

思路2：不把整数转为字符串，直接用整数类型来判断是否是回文数。如果一个数字为正整数，而且能够被 10 整除，那么这个数字也不是回文数，因为回文数的首位肯定不是 0 。实现方案：直接把整数反转过来，与原来的值比较即可。时间复杂度: O(1)，空间复杂度: O(1)

// go-algo-demo/algo01/demo2.go
func isPalindrome2(x int) bool {
	// 负数肯定不是palindrome
	// 如果一个数字是一个正数，并且能被10整除，那它肯定也不是palindrome，因为首位肯定不是 0
	if x < 0 || (x != 0 && x%10 == 0) {
		return false
	}
	rev, y := 0, x
	for x > 0 {
		rev = rev*10 + x%10
		x /= 10
	}
	return y == rev
}

func main() {
	fmt.Println(isPalindrome2(12321)) //true
	fmt.Println(isPalindrome2(1212))  //false
}

参考源代码：https://gitee.com/rxbook/go-algo-demo/tree/master/algo01