多元线性回归模型
1. 建立模型:模型函数
Y ^ = W T X \hat{Y} = W^TX Y^=WTX
如果有 n+1 条数据,每条数据有 m+1 种x因素(每种x因素都对应 1 个权重w),则
👉已知数据:实际Y值=
[
y
0
y
1
y
2
y
3
.
.
.
y
n
]
\begin{bmatrix}y_0\\y_1\\y_2\\y_3\\...\\y_n\end{bmatrix}
y0y1y2y3...yn
,X=
[
x
00
,
x
10
.
.
.
x
m
0
x
01
,
x
11
.
.
.
x
m
1
x
02
,
x
12
.
.
.
x
m
2
x
03
,
x
13
.
.
.
x
m
3
.
.
.
x
0
n
,
x
1
n
.
.
.
x
m
n
]
\begin{bmatrix}x_{00},x_{10}...x_{m0}\\x_{01},x_{11}...x_{m1}\\x_{02},x_{12}...x_{m2}\\x_{03},x_{13}...x_{m3}\\...\\x_{0n},x_{1n}...x_{mn}\end{bmatrix}
x00,x10...xm0x01,x11...xm1x02,x12...xm2x03,x13...xm3...x0n,x1n...xmn
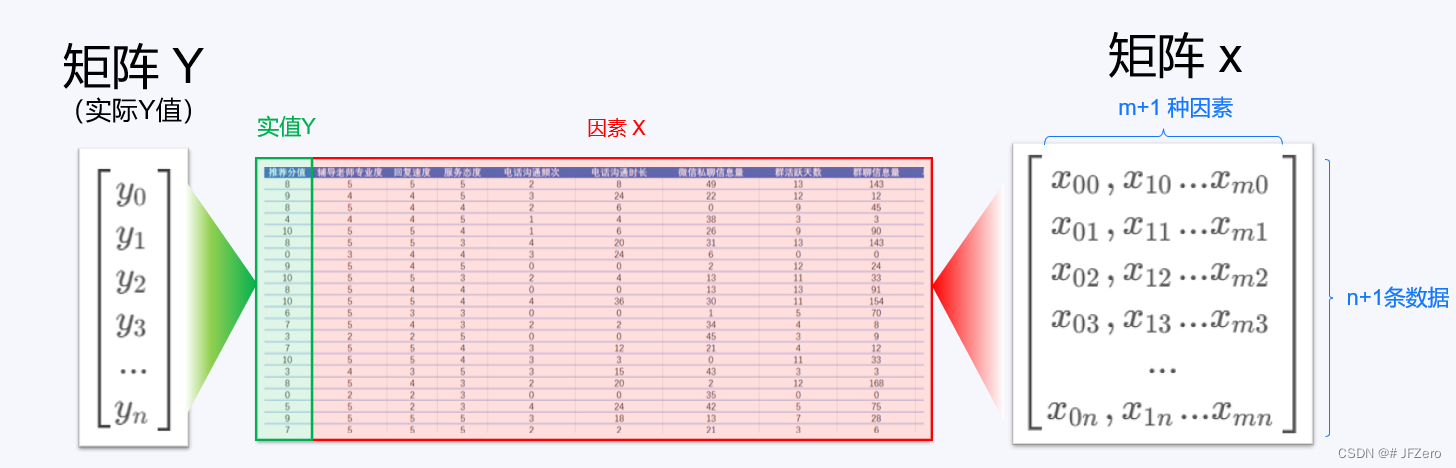
👉未知数据:模型
Y
^
\hat{Y}
Y^值=
[
y
0
^
y
1
^
y
2
^
.
.
.
y
n
^
]
\begin{bmatrix}\hat{y_0}\\ \hat{y_1}\\\hat{y_2}\\...\\\hat{y_n}\end{bmatrix}
y0^y1^y2^...yn^
模型参数 W=
[
w
0
,
w
1
,
w
2
,
w
3
,
.
.
.
,
w
m
]
\begin{bmatrix}w_0,w_1,w_2,w_3,...,w_m\end{bmatrix}
[w0,w1,w2,w3,...,wm]
2. 学习模型:损失函数
2.1 损失函数-最小二乘法
Loss = ∑ ( y ^ i 计算 − y i 实际 ) 2 ∑(\hat{y}_{i计算}-y_{i实际})² ∑(y^i计算−yi实际)2
Y
计算
^
\hat{Y_{计算}}
Y计算^=
[
y
0
^
y
1
^
y
2
^
.
.
.
y
n
^
]
\begin{bmatrix}\hat{y_0}\\ \hat{y_1}\\\hat{y_2}\\...\\\hat{y_n}\end{bmatrix}
y0^y1^y2^...yn^
, 实际Y值=
[
y
0
y
1
y
2
.
.
.
y
n
]
\begin{bmatrix}y_0\\y_1\\y_2\\...\\y_n\end{bmatrix}
y0y1y2...yn
,
Y
计算
^
−
Y
\hat{Y_{计算}} -Y
Y计算^−Y=
[
y
0
^
−
y
0
y
1
^
−
y
1
y
2
^
−
y
2
.
.
.
y
n
^
−
y
n
]
\begin{bmatrix}\hat{y_0}-y_0\\ \hat{y_1}-y_1\\\hat{y_2}-y_2\\...\\\hat{y_n}-y_n\end{bmatrix}
y0^−y0y1^−y1y2^−y2...yn^−yn
则Loss =
[
y
0
^
−
y
0
,
y
1
^
−
y
1
,
y
2
^
−
y
2
,
.
.
.
,
y
n
^
−
y
n
]
[
y
0
^
−
y
0
y
1
^
−
y
1
y
2
^
−
y
2
.
.
.
y
n
^
−
y
n
]
\begin{bmatrix}\hat{y_0}-y_0, \hat{y_1}-y_1,\hat{y_2}-y_2,...,\hat{y_n}-y_n\end{bmatrix}\begin{bmatrix}\hat{y_0}-y_0\\ \hat{y_1}-y_1\\\hat{y_2}-y_2\\...\\\hat{y_n}-y_n\end{bmatrix}
[y0^−y0,y1^−y1,y2^−y2,...,yn^−yn]
y0^−y0y1^−y1y2^−y2...yn^−yn
Loss =
(
Y
计算
^
−
Y
)
T
(
Y
计算
^
−
Y
)
(\hat{Y_{计算}} -Y)^T(\hat{Y_{计算}} -Y)
(Y计算^−Y)T(Y计算^−Y)
👉 Y 计算 ^ = W T X \hat{Y_{计算}} = W^TX Y计算^=WTX,因此 Loss = ( W T X − Y ) T ( W T X − Y ) (W^TX-Y)^T(W^TX-Y) (WTX−Y)T(WTX−Y)
( W T X − Y ) T = ( W T X ) T − Y T = X T W − Y T (W^TX-Y)^T=(W^TX)^T-Y^T= X^TW-Y^T (WTX−Y)T=(WTX)T−YT=XTW−YT
则 Loss = ( X T W − Y T ) ( W T X − Y ) = X T W W T X − Y T W T X − X T W Y + Y T Y (X^TW-Y^T)(W^TX-Y)=X^TWW^TX-Y^TW^TX-X^TWY+Y^TY (XTW−YT)(WTX−Y)=XTWWTX−YTWTX−XTWY+YTY
2.2 损失函数-求导解析解
👉
∂
(
L
o
s
s
)
∂
(
W
)
=
∂
(
X
T
W
W
T
X
)
∂
(
W
)
−
∂
(
Y
T
W
T
X
)
∂
(
W
)
−
∂
(
X
T
W
Y
)
∂
(
W
)
+
∂
(
Y
T
Y
)
∂
(
W
)
\frac{∂(Loss)}{∂(W)} =\frac{∂(X^TWW^TX)}{∂(W)}-\frac{∂(Y^TW^TX)}{∂(W)}-\frac{∂(X^TWY)}{∂(W)}+\frac{∂(Y^TY)}{∂(W)}
∂(W)∂(Loss)=∂(W)∂(XTWWTX)−∂(W)∂(YTWTX)−∂(W)∂(XTWY)+∂(W)∂(YTY)
根据以下矩阵求导证明:

👉 ∂ ( L o s s ) ∂ ( W ) = ∂ ( X T W W T X ) ∂ ( W ) − ∂ ( Y T W T X ) ∂ ( W ) − ∂ ( X T W Y ) ∂ ( W ) + ∂ ( Y T Y ) ∂ ( W ) \frac{∂(Loss)}{∂(W)} =\frac{∂(X^TWW^TX)}{∂(W)}-\frac{∂(Y^TW^TX)}{∂(W)}-\frac{∂(X^TWY)}{∂(W)}+\frac{∂(Y^TY)}{∂(W)} ∂(W)∂(Loss)=∂(W)∂(XTWWTX)−∂(W)∂(YTWTX)−∂(W)∂(XTWY)+∂(W)∂(YTY)
👉 ∂ ( L o s s ) ∂ ( W ) = 2 X X T W − 2 X Y T \frac{∂(Loss)}{∂(W)} =2XX^TW-2XY^T ∂(W)∂(Loss)=2XXTW−2XYT
👉当 ∂ ( L o s s ) ∂ ( W ) = 0 ,则 W = 1 2 ∗ ( X X T ) − 1 ( 2 X Y T ) = ( X X T ) − 1 ( X Y T ) \frac{∂(Loss)}{∂(W)}=0,则W =\frac{1}{2}*(XX^T)^{-1}(2XY^T)=(XX^T)^{-1}(XY^T) ∂(W)∂(Loss)=0,则W=21∗(XXT)−1(2XYT)=(XXT)−1(XYT)
当 ( X X T ) − 1 (XX^T)^{-1} (XXT)−1计算时,只有当 X X T XX^T XXT为满秩矩阵时,W才有解
当
W
=
1
2
∗
(
X
X
T
)
−
1
(
2
X
Y
T
)
=
(
X
X
T
)
−
1
(
X
Y
T
)
W =\frac{1}{2}*(XX^T)^{-1}(2XY^T)=(XX^T)^{-1}(XY^T)
W=21∗(XXT)−1(2XYT)=(XXT)−1(XYT)时,👉
∂
(
L
o
s
s
)
∂
(
W
)
=
0
\frac{∂(Loss)}{∂(W)}=0
∂(W)∂(Loss)=0,仅仅能证明Loss取到极值,并不能说明是极小值,还是极大值!
因此,要如何判断Loss是极大值还是极小值?
当Loss处于极小值点时,一阶导
L
o
s
s
′
=
d
(
L
o
s
s
)
W
=
0
Loss^{'}=\frac{d(Loss)}{W}=0
Loss′=Wd(Loss)=0,二阶导
L
o
s
s
′
′
>
0
Loss^{''}>0
Loss′′>0
当Loss处于极大值点时,一阶导
L
o
s
s
′
=
d
(
L
o
s
s
)
W
=
0
Loss^{'}=\frac{d(Loss)}{W}=0
Loss′=Wd(Loss)=0,二阶导
L
o
s
s
′
′
<
0
Loss^{''}<0
Loss′′<0
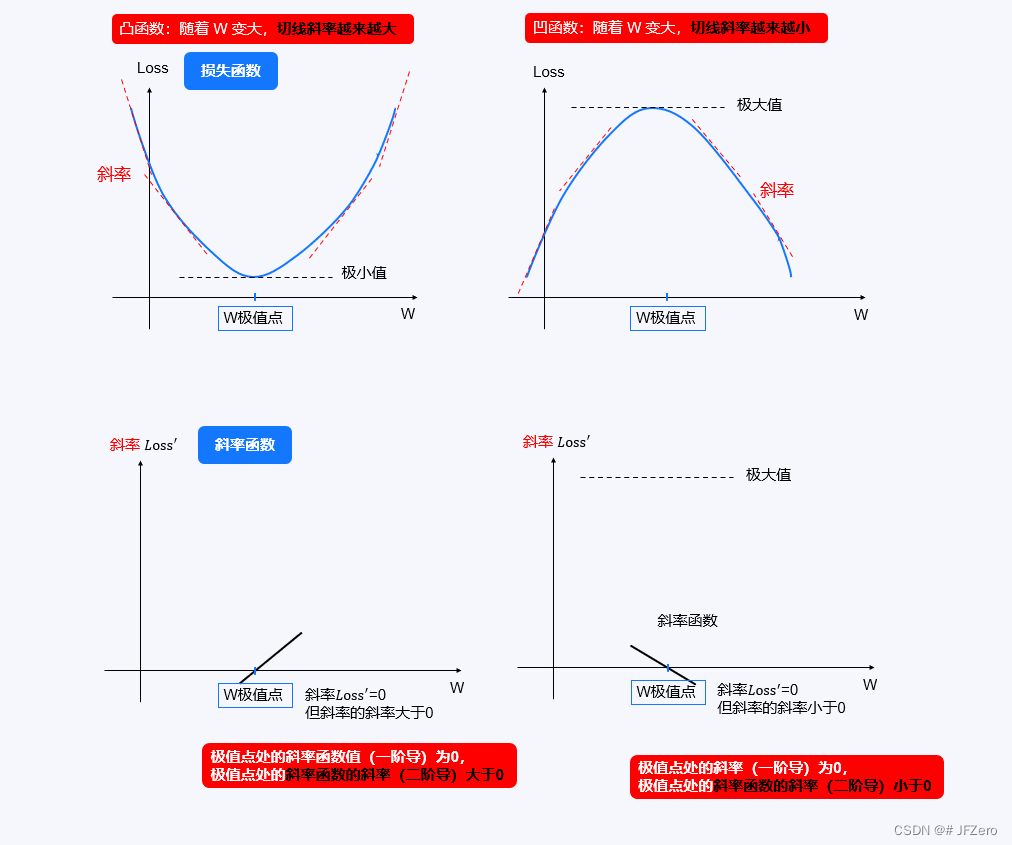
已知最小二乘法损失函数一阶导
L
o
s
s
′
=
d
(
L
o
s
s
)
W
=
∂
(
L
o
s
s
)
∂
(
W
)
=
2
X
X
T
W
−
2
X
Y
T
Loss^{'}=\frac{d(Loss)}{W}=\frac{∂(Loss)}{∂(W)} =2XX^TW-2XY^T
Loss′=Wd(Loss)=∂(W)∂(Loss)=2XXTW−2XYT
则二阶导为
L
o
s
s
′
′
=
d
(
2
X
X
T
W
−
2
X
Y
T
)
W
=
2
X
X
T
=
2
∗
[
x
00
,
x
10
.
.
.
x
m
0
x
01
,
x
11
.
.
.
x
m
1
x
02
,
x
12
.
.
.
x
m
2
x
03
,
x
13
.
.
.
x
m
3
.
.
.
x
0
n
,
x
1
n
.
.
.
x
m
n
]
[
x
00
,
x
01
.
.
.
x
0
n
x
10
,
x
11
.
.
.
x
1
n
x
20
,
x
21
.
.
.
x
2
n
x
30
,
x
31
.
.
.
x
3
n
.
.
.
x
m
0
,
x
m
1
.
.
.
x
m
n
]
=
[
x
00
2
,
.
.
.
,
.
.
.
,
.
.
.
,
.
.
.
.
.
.
,
x
11
2
.
.
.
.
,
.
.
.
,
.
.
.
.
.
.
,
.
.
.
,
x
33
2
,
.
.
.
,
.
.
.
.
.
.
,
.
.
.
,
.
.
.
,
.
.
.
,
x
m
n
2
]
Loss^{''}=\frac{d(2XX^TW-2XY^T)}{W}=2XX^T=2*\begin{bmatrix}x_{00},x_{10}...x_{m0}\\x_{01},x_{11}...x_{m1}\\x_{02},x_{12}...x_{m2}\\x_{03},x_{13}...x_{m3}\\...\\x_{0n},x_{1n}...x_{mn}\end{bmatrix}\begin{bmatrix}x_{00},x_{01}...x_{0n}\\x_{10},x_{11}...x_{1n}\\x_{20},x_{21}...x_{2n}\\x_{30},x_{31}...x_{3n}\\...\\x_{m0},x_{m1}...x_{mn}\end{bmatrix}=\begin{bmatrix}x_{00}²,...,...,...,...\\...,x_{11}²....,...,...\\...,...,x_{33}²,...,\\...\\...,...,...,...,x_{mn}²\end{bmatrix}
Loss′′=Wd(2XXTW−2XYT)=2XXT=2∗
x00,x10...xm0x01,x11...xm1x02,x12...xm2x03,x13...xm3...x0n,x1n...xmn
x00,x01...x0nx10,x11...x1nx20,x21...x2nx30,x31...x3n...xm0,xm1...xmn
=
x002,...,...,...,......,x112....,...,......,...,x332,...,......,...,...,...,xmn2
由于主元全为正数,且矩阵对称,因此二阶导数矩阵为正定实对称矩阵,特征值全大于0
马马虎虎…地…对于正定矩阵、实对称矩阵已经懵圈