学习前两章内容，主要是围绕孪生网络展开

0 封面

1 第一章：元学习简介

1. 随着生成对抗网络和胶囊网络等优秀算法的出现，深度学习得到了快速的发展。
2. 但是使用深度学习网络解决A任务时，假设A任务和B任务接近，但是深度神经网络也是要从头开始训练B任务的。
3. 元学习的目的是：“让机器学会学习”。也就是对于一个新任务，元学习模型可以利用之前从相关任务中获得的知识，也就是说无需从零开始训练。

1.1 元学习与少样本学习

1. 少样本学习（few-shot learning）或k 样本学习（k-shot learning）指的是利用较少的数据点进行学习，其中k 表示数据集各个类别中数据点的数量。
2. 单样本学习：一张猫，一张狗
3. 10样本学习：十张猫，十张狗

1.2 元学习的类型——学习度量空间

1. 在基于度量的元学习场景中，学习合适的度量空间。
2. 基于度量的场景中，使用一个简单的神经网络从两幅图像中提取特征（第一步），并通过计算两幅图像特征之间的距离找到相似性。
3. 这种方法被广泛应用于数据点较少的少样本学习中。

1.3 学习初始化

• 一般的：我们首先初始化随机权重，计算损失，并通过梯度下降来最小化损失。因此，我们将通过梯度下降找到最优权重，使损失最小。
• 元学习：不随机初试化权重，而是使用最优值或者接近最优质的值来初试化权重，那么就可以更快的收敛，并快速学习。

1.4 学习优化器

• 一般如何优化神经网络呢？——通过基于大数据集的训练来优化升级网络，并使用梯度下降来最小化损失。
• 在少样本的学习场景中：梯度下降失效了，由于数据集小。所以我们学习优化器本身。

A：试图学习的基网络
B：优化基网络的元网络

1.5 通过梯度下降来学习如何通过梯度下降来学习

1. 基础知识：元学习是让机器学会学习。
2. 一般的，我们都是通过梯度下降来计算损失和最小化损失，以训练神经网络。所以是使用梯度下降来优化模型。
3. 在元学习中，梯度下降失效了，我们能自动学习这个过程吗？

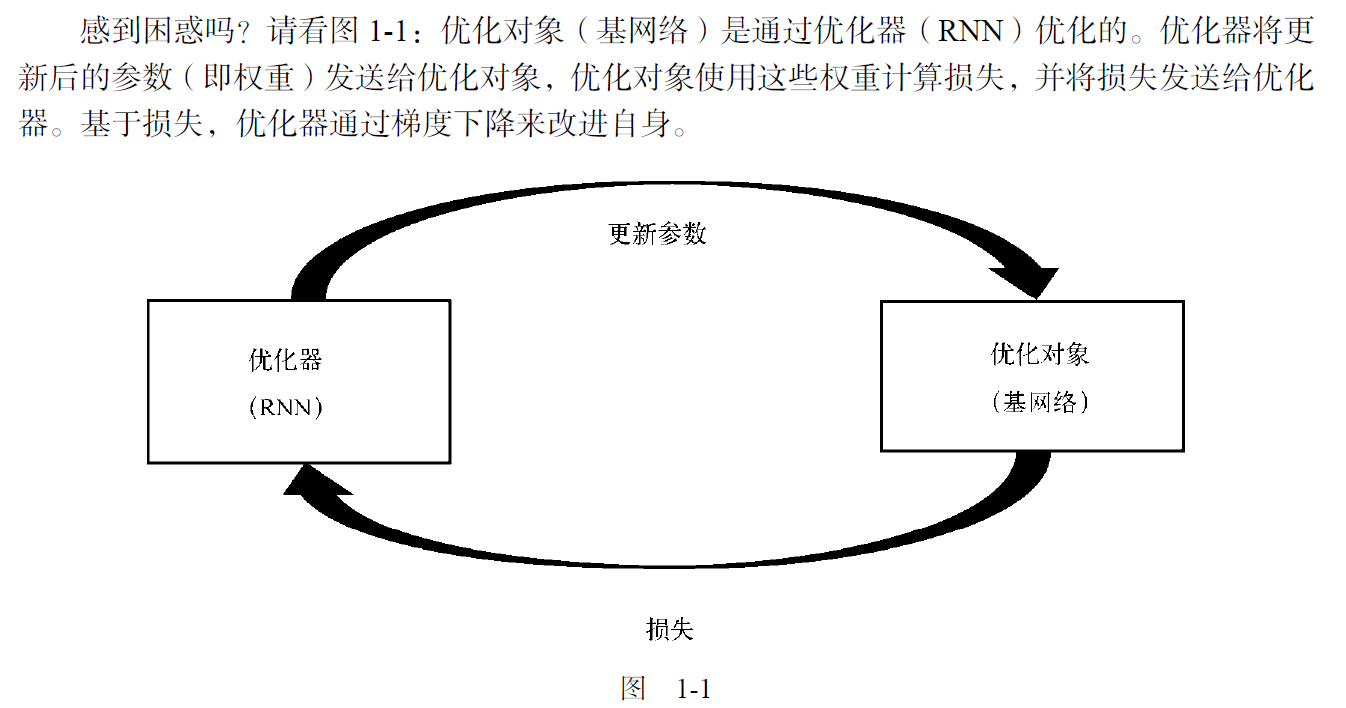
用递归神经网络（RNN）来代替传统的梯度下降优化器。

中心思想：用RNN 代替梯度下降法。
那么如何优化RNN呢？——用梯度下降法。

也就是说，元学习模型用RNN来优化模型，其中RNN的优化需要依靠梯度下降法。
也就解释了通过梯度下降（训练RNN）来学习如何通过梯度下降来学习

称RNN为优化器，基网络为优化对象。

---

2 第二章：使用孪生网络进行人脸识别与音频视频

孪生神经网络：基于度量的单样本学习算法，如何从很少数据点中学习，以及如何来解决低数据问题。

2.1 什么是孪生神经网络

1. 孪生神经网络主要用于各类别数据点较少的应用中。

2. 孪生神经网络大致上由两个对称的神经网络组成，它们具有相同的权重和架构，最后由能量函数 $E$ 连接在一起。

3. 孪生神经网络的目标是——了解两个输入值是否相似。

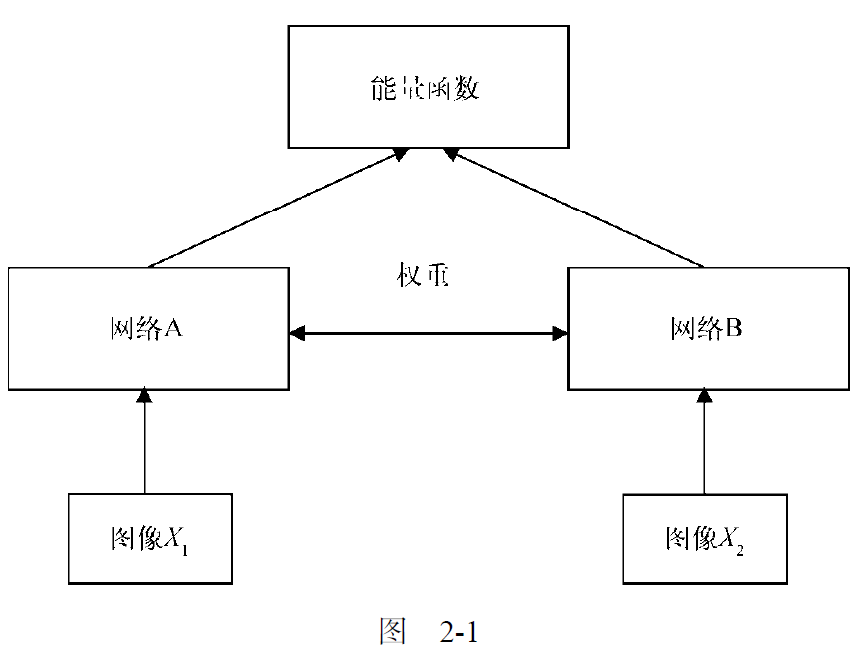
孪生神经网络的架构图

• 网络A 和网络B 具有相同的权重和架构，作用是为输入数据生成嵌入(embedding)，即特征向量(feature vector)。因此可以使用任意产生嵌入的网络。【也就是说要提取特征】

• 能量函数会输出这两个输入的相似程度，可以使用任意相似性度量，如欧式距离或余弦相似度。

总的来说，孪生网络不仅用于人脸识别，还 广泛用于数据点较少的应用以及需要学习两个输入之间相似性的任务中。

2.1.1 孪生网络的架构

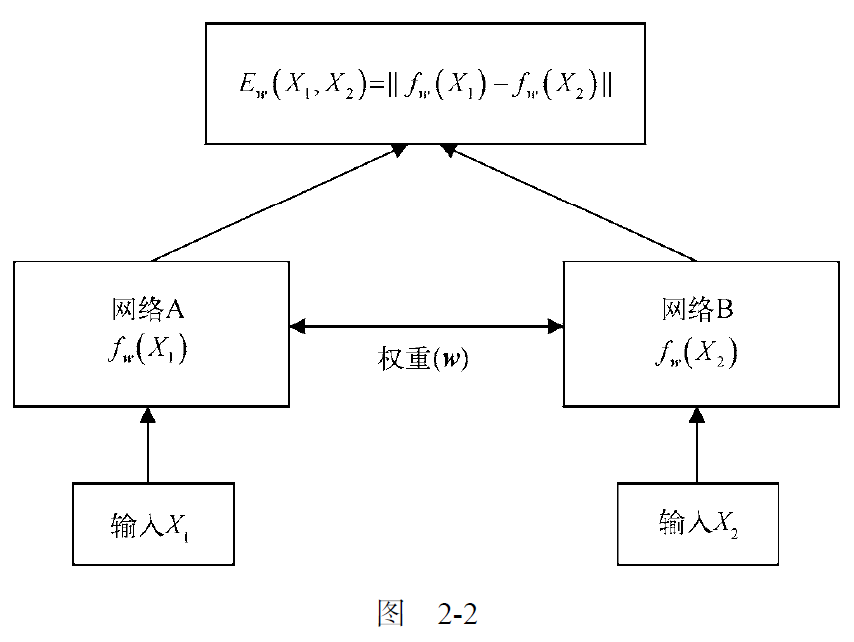
从上图可以看出，能量函数选择的是欧式距离。

欧式距离对应l2范数。

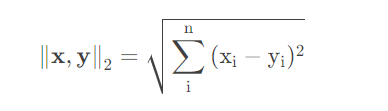
如何训练孪生神经网络呢？
数据如何组织呢？
特征和标签是什么呢？
我们的目标函数是什么呢？

我们的损失函数是什么呢？
由于孪生网络的目标不是执行分类任务，而是理解两个输入值之间的相似性，因此我们使用了对比损失函数。

2.2 使用孪生网络进行人脸识别

孪生网络的目的是了解两张脸相似与否。

数据集建立

数据格式：输入值成对，并且带有标签

---

有了成对的数据以及标签，就可以训练孪生网络了。

• 第一步：我们将图像对中的一个图像输入网络A，另一个图像输人网络B。这两个网络的作用只是提取特征向量。

• 第二步：我们使用带有整流线性单元 ( rectified linear unit, ReLU ) 激活函数的两个卷积层提取特征。

• 第三步：把两个网络输出的特征向量输入能量函数，用于测量相似度(用欧氏距离作为能量函数)。

因此，我们通过输入图像对来训练网络，以学习它们之间的语义相似度。

至此，训练集和测试集已经成功生成。

构建孪生网络

首先定义基网络：用于提取特征的卷积网络

我们建立两个均带有ReLU 激活函数和最大池化（max pooling）的卷积层与一个扁平化层（flat layer）：

def build_base_network(input_shape):
	seq = Sequential()  # 线性层
	nb_filter = [6, 12]
	kernel_size = 3
	#卷积层1
	seq.add(Convolution2D(nb_filter[0], kernel_size, kernel_size,input_shape=input_shape,border_mode='valid', dim_ordering='th'))  # 2维卷积，过滤器是6*3*3
	seq.add(Activation('relu'))  # relu激活
	seq.add(MaxPooling2D(pool_size=(2, 2)))  # 最大池化
	seq.add(Dropout(.25)) # dropout层
	
	#卷积层2
	seq.add(Convolution2D(nb_filter[1], kernel_size,kernel_size,border_mode='valid', dim_ordering='th'))  # 2维卷积，过滤器是12*3*3
	seq.add(Activation('relu'))
	seq.add(MaxPooling2D(pool_size=(2, 2),dim_ordering='th'))
	seq.add(Dropout(.25))
	
	#扁平化层
	seq.add(Flatten())
	seq.add(Dense(128, activation='relu'))
	seq.add(Dropout(0.1))
	seq.add(Dense(50, activation='relu'))
	return seq

把图像输入基网络，基网络返回嵌入，即特征向量。

其次定义能量函数，计算距离

这里选取欧式距离作为能量函数：

def euclidean_distance(vects):
	x, y = vects
	return K.sqrt(K.sum(K.square(x - y), axis=1, keepdims=True))

选择优化函数，并定义模型

epochs = 13
rms = RMSprop()
model = Model(input=[input_a, input_b], output=distance)

选择损失函数，并编译模型

def contrastive_loss(y_true, y_pred):
	margin = 1
	return K.mean(y_true * K.square(y_pred) + (1 - y_true) *  K.square(K.maximum(margin - y_pred, 0)))
	
model.compile(loss=contrastive_loss, optimizer=rms)

定义一个函数来计算准确率

def compute_accuracy(predictions, labels):
	return labels[predictions.ravel() < 0.5].mean()

2.3 使用孪生网络进行音频识别

那么如何将这些原始音频输入网络中呢？
如何从原始音频中提取有意义的特征呢？

众所周知，神经网络只接受向量化的输入，因此需要将音频转换为数组输入，再转化为特征向量。

然后就是打标签的过程了，省略。

注意：由于不同音频的音频嵌入长度各不相同，假设最大程度为400，小于400则使用0来填充。

构建基网络

使用3个dense层，中间有一个dropout层。

def build_base_network(input_shape):
	input = Input(shape=input_shape)
	x = Flatten()(input)
	x = Dense(128, activation='relu')(x)
	x = Dropout(0.1)(x)
	x = Dense(128, activation='relu')(x)
	x = Dropout(0.1)(x)
	x = Dense(128, activation='relu')(x)
	return Model(input, x)

使用欧式距离作为能量函数

def euclidean_distance(vects):
	x, y = vects
	return K.sqrt(K.sum(K.square(x - y), axis=1, keepdims=True))

确定优化函数

epochs = 13
rms = RMSprop()
model = Model(input=[audio_a, audio_b], output=distance)

确定损失函数

def contrastive_loss(y_true, y_pred):
	margin = 1
	return K.mean(y_true * K.square(y_pred) + (1 - y_true) * K.square(K.maximum(margin - y_pred, 0)))

model.compile(loss=contrastive_loss, optimizer=rms)