位运算
常见的位运算 >>、>>>、<<、|、&、^、||、&&、~等
原码、反码、补码
-
原码
将一个整数转换成二进制形式,就是其原码。例如 6 原码就是……0000 0000 0000 0110 -
反码
对于正数,它的反码就是其原码(原码和反码相同);负数的反码是将原码中除符号位以外的所有位(数值位)取反,也就是 0 变成 1,1 变成 0。例如 6的原码和反码都是……0000 0000 0000 0110;反码 …… 1111 1111 1111 1001 -
补码
对于正数,它的补码就是其原码(原码、反码、补码都相同);负数的补码是其反码加 1。
补码是在反码的基础上打了一个补丁,所以叫“补码”。
数的二进制表示
正数:就是其二进制表示 (原码)
0 : 0000000…… 0
负数:去掉符号位后 二进制的补码
为什么java中负数的值是去掉符号位后 二进制的补码
就是这样设计的,也是系统底层为了运算,与非门计算的时候通过一套逻辑运算,不用走多个分支,可以直接进行二进制的加法运算
输出int类型数字二进制形式
public void print(int number) {
for (int i = 31; i >= 0; i--) {
System.out.print((number & (1 << i)) == 0 ? "0" : "1");
}
System.out.println();
}
}
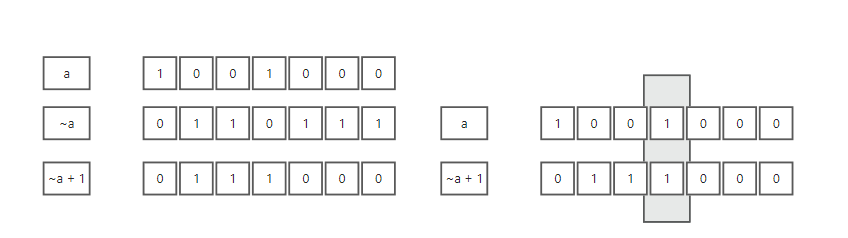
求相反数
int a = 10;
~a + 1 = -10
二进制取反在 + 1 即可
找到数字二进制最后一位1
a & (~a + 1) = a & (-a)
a & ~a 的结果是所有位数都是 0
(~a + 1) 就是为了补上这一位,然后提取a二进制的最后一位 1
位运算实战
不用中间变量交换两个数
使用异或操作 二进制为 相同为0,不同为1 ,^ 满足交换律与结合律
结论1:一个数 ^ 自己 = 0 ( a ^ a = 0)
结论2:一个数 ^ 0 = 当前数 (a ^ 0 = a)
结论3:a ^ b ^ a = b => (a ^ a ^ b) = b
交换过程
num1 = num1 ^ num2;
num2 = num1 ^ num2;
num1 = num2 ^ num1;
交换过程:
初始条件 => num1 = A num2 = B
1,num1 = A ^ B ; 此时 num1值已经改变为A ^ B
2,num2 = num1 ^ num2 => A ^ B ^ B = > A 此时num2的值改变为 A
3,num1 = num2 ^ num1 => A ^ A ^ B = > B 完成值交换

public static void exchangeTwoNumber(int num1,int num2){
num1 = num1 ^ num2;
num2 = num1 ^ num2;
num1 = num2 ^ num1;
System.out.println( num1 + " *** " + num2);
}
一组数找到出现奇数次的数
在一组数种有一种数出现了奇数次,其他数字全部出现偶数次,找出出现奇数次数的数字
- 一种数出现奇数次 a
思路 :相同的数 ^ 为0 ,任何一个数 ^ 0 等于那个数 ,可以将所有的数 ^ 剩下的就是 奇数次的数 a
- 两种数出现奇数次 分别为 a 和 b 例: (11 22 33 4 5)
思路:
1,将所有的数 ^ 结果是剩下的两种奇数次 a ^ b 的值 res
2,因为a != b 所以 res != 0
3,取出 res 二进制中最后一位 1 ,把这个位置记为 X 位 (当然取任何一位1 都可以 为什么要取这一个1?)
4,因为 在这个 1 的 X位置上 a 和 b 的值是不一样的 (一个是 1 一个是 0)
5,现在假设 a 的X 位置为 1 b的X位置 为 0 ( a的X 位置为0 ,b X位置为1 也可以)
6,所以可以把 所有的数分为两类 这个位置上的数字是 1的 和是 0 的 ( a 和其他出现偶数次数的 X位置为1的 | b 和其他出现偶数次的 X位置为 0的 )
7,现在把 a 和其他出现偶数次数的 X位置为1的 进行 ^ 运算 就求出了 找到了a
8,res ^ a = b

/**
* 一种数出现了奇数次,其他数出现了偶数次 找到这个数
*/
public static int getOddOne(int arr[]) {
int odd = 0;
for (int i = 0; i < arr.length; i++) {
odd = odd ^ arr[i];
}
return odd;
}
/**
* 两种数出现了奇数次,其他数出现了偶数次 找到这个数
*/
public static int[] getOddTwo(int arr[]) {
int resArr[] = new int[2];
int res = 0;
for (int i = 0; i < arr.length; i++) {
res = res ^ arr[i];
}
int resEnd = res & (~res + 1);
int resTemp = 0;
for (int i = 0; i < arr.length; i++) {
// 相同位置为 1
if ((arr[i] & resEnd) == 1) {
resTemp ^= arr[i];
}
}
resArr[0] = resTemp;
resArr[1] = resTemp ^ res;
return resArr;
}
找到出现次数K次数的数
一组int类型数字中有一个数字出现了K次,其他数字出现了M次,M > 1 K < M 找到出现了K次的数
要求,额外空间复杂度 O(1), 时间复杂度 O(N)
思路:
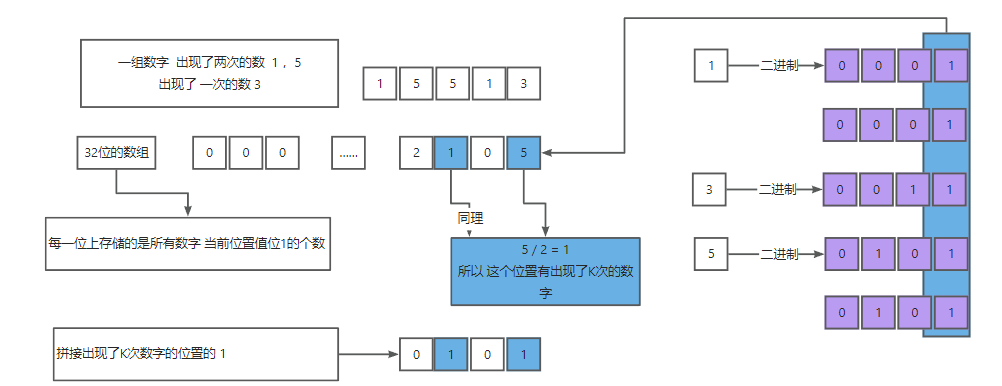
1,定义一个长度为 32 的数组arr , 装的是所有数字 每一个位置 值为 1的个数 (解释见下图)
2,每一个位置中的数字个数,一定为 M的整数倍,或者 M的整数倍 + K 因为 K< M
3,所有值为 1的个数为 M的整数倍 + K 说明K的二进制在当前位置有值
4,将K的所有二进制位数拼接在一起,就找到了这个数
扩展
一组int类型数字中,其他数字出现了M次,剩下那一个数字如果出现了K次,返回这个数,如果没出现K次,返回 - 1
难点:如果出现了K次的数字是0,不会有 二进制为1的位置存入二进制数组,要单独处理
public class BitKM {
public static void main(String[] args) {
// int[] arr2 = {2, 2 ,2 ,6 ,6 ,6,3};
// int i = getKNumber(arr2, 1, 3);
// System.out.println(i);
int maxKinds = 100;
int k = 7;
int m = 8;
int range = 200;
// for (int j = 0; j < 1000; j++) {
// int[] randomArr = getRandomArr(maxKinds, range, k, m);
// int mapValue = myHashMapTest(randomArr, k, m);
// int kNumber = getKNumber(randomArr, k, m);
// if(mapValue != kNumber){
// System.out.println(mapValue);
// System.out.println(kNumber);
// System.out.println("出错了 " );
// }
// }
// System.out.println(" no problem");
for (int j = 0; j < 1000; j++) {
int[] randomArr = getRandomArrForIfHasK(maxKinds, range, k, m);
int mapValue = myHashMapTest(randomArr, k, m);
int kNumber = getKNumberIfHas(randomArr, k, m);
if(mapValue != kNumber){
System.out.println(mapValue);
System.out.println(kNumber);
System.out.println("出错了 " );
}
}
System.out.println(" no problem");
}
// arr种 找出出现k次的数
public static int getKNumber(int arr[],int k,int m){
int [] arrRes = new int[32];
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < 32; j++) {
// 1010101
// if(((arr[i] >> j) & 1) == 1){
// arrRes[j] ++;
// }
arrRes[j]+= (arr[i] >> j) & 1;
}
}
int res = 0;
for (int i = 0; i < 32; i++) {
if(arrRes[i] % m == k){
res |= (1 << i);
}
}
return res;
}
// arr种 如果有出现k次的数 返回 否则 返回 -1
public static int getKNumberIfHas(int arr[],int k,int m){
int [] arrRes = new int[32];
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < 32; j++) {
// 1010101
// if(((arr[i] >> j) & 1) == 1){
// arrRes[j] ++;
// }
arrRes[j]+= (arr[i] >> j) & 1;
}
}
int res = 0;
for (int i = 0; i < 32; i++) {
if (arrRes[i] % m !=0 ){
if(arrRes[i] % m == k){
res |= (1 << i);
} else {
return -1;
}
}
}
if (res == 0){
int count = 0;
for(int num : arr){
if(num == 0){
count ++;
}
}
if(count != k){
return -1;
}
}
return res;
}
public static int myHashMapTest(int [] arr ,int k,int m){
// HashMap< 数字,出现的次数 >
HashMap<Integer,Integer> hashMap = new HashMap<>();
for (int i = 0; i < arr.length; i++) {
Integer orDefault = hashMap.getOrDefault(arr[i], 0);
hashMap.put(arr[i] , ++orDefault);
}
for (int num : hashMap.keySet()){
if(hashMap.get(num) == k){
return num;
}
}
return -1;
}
public static int[] getRandomArr(int maxKinds,int range, int k, int m){
// 出现了K次的数
int kNum = getRangeNumber(range);
int kinds = (int)(Math.random() * maxKinds) + 2;
int [] arrRes = new int[ k + m * (kinds - 1)];
HashSet<Integer> hashSet = new HashSet<>();
int index = 0;
for (int i = 0; i < k; i++) {
arrRes[index++] = kNum;
}
hashSet.add(kNum);
kinds--;
while (kinds > 0){
int num;
do {
num = getRangeNumber(range);
} while (hashSet.contains(num));
hashSet.add(num);
kinds--;
for (int i = 0; i < m; i++) {
arrRes[index++] = num;
}
}
for (int i = 0; i < arrRes.length; i++) {
int change = (int) (Math.random() * arrRes.length);
int temp = arrRes[i];
arrRes[i] = arrRes[change];
arrRes[change] = temp;
}
return arrRes;
}
public static int[] getRandomArrForIfHasK(int maxKinds,int range, int k, int m){
// 出现了K次的数
int kNum = getRangeNumber(range);
int kTimes = Math.random() < 0.5 ? k : (int) ((Math.random() * (m - 1))+ 1);
int kinds = (int)(Math.random() * maxKinds) + 2;
int [] arrRes = new int[ kTimes + m * (kinds - 1)];
HashSet<Integer> hashSet = new HashSet<>();
int index = 0;
for (int i = 0; i < kTimes; i++) {
arrRes[index++] = kNum;
}
hashSet.add(kNum);
kinds--;
while (kinds > 0){
int num;
do {
num = getRangeNumber(range);
} while (hashSet.contains(num));
hashSet.add(num);
kinds--;
for (int i = 0; i < m; i++) {
arrRes[index++] = num;
}
}
for (int i = 0; i < arrRes.length; i++) {
int change = (int) (Math.random() * arrRes.length);
int temp = arrRes[i];
arrRes[i] = arrRes[change];
arrRes[change] = temp;
}
return arrRes;
}
// [-range, +range]
public static int getRangeNumber(int range){
return (int) (Math.random() * (range + 1) - (int)(Math.random() * (range + 1)));
}
}
点个赞呗






![[附源码]计算机毕业设计springboot吾悦商城管理系统](https://img-blog.csdnimg.cn/881063ae189d4fc1b224d93bfc543c15.png)

![[附源码]Python计算机毕业设计Django和vue的茶文化交流平台的设计与实现](https://img-blog.csdnimg.cn/d2fa344d32e94e2eafe0a78ca222a842.png)

![[附源码]计算机毕业设计在线招聘网站Springboot程序](https://img-blog.csdnimg.cn/852f4fedf8ba4a0cbccf3eb09be3fe38.png)


![[附源码]JAVA毕业设计互联网保险网站(系统+LW)](https://img-blog.csdnimg.cn/248308f8b2354404b3da403ee2c25f44.png)