【POJ No. 2777】 颜色统计 Count Color

北大OJ 题目地址

【题意】

有一个长L 厘米的电路板，可以将板均分为L 段（1～L ），每段长1厘米。现在给电路板上色，每段只有一种颜色。可以在电路板上执行两种操作：①C a b c ，从a 段到b 段涂色为c ；②P a b ，输出a 段和b 段之间不同颜色的数量（包括a 、b），颜色编号为1～T 。

开始时，在电路板上涂有颜色1。

【输入输出】

输入：

第1行包含3个整数L （1≤L ≤105 ）、T （1≤T ≤30）和O （1≤O ≤105 ，表示操作次数）。接下来的O 行，每行都包含C a b c 或P a b （a 、b 、c 是整数，a 可以大于b ）。

输出：

按顺序单行输出操作结果。

【样例】

【思路分析】

根据输入样例，长度L =2，颜色数T =2，操作次数O =4，初始时均为1号色。

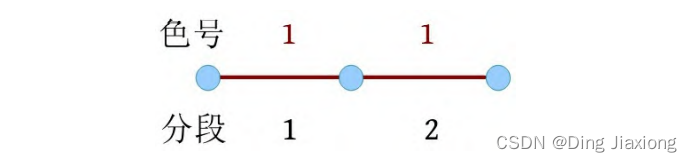
① C 1 1 2：将1-1段涂2号色。

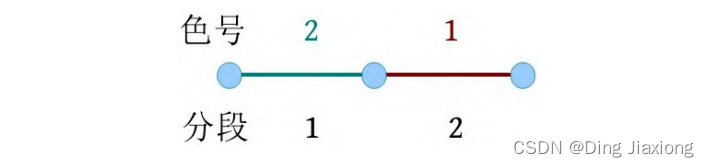
② P 1 2：统计1-2段的颜色数，输出颜色数2。

③ C 2 2 2：将2-2段涂2号色。

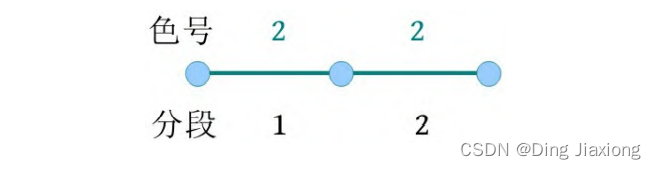
④ P 1 2：统计1-2段的颜色数，输出颜色数1。

这道题包括区间修改、区间查询，可以用线段树解决。

由于这题的区间查询只需统计该区间的颜色数，因此并不需要将区间内的所有颜色求和。

【 算法设计】

① 创建线段树，树根的颜色为1（相当于懒标记），其他节点的颜色为0。

② 查询[l , r ]区间的颜色数。若树根rt颜色不为0，则ans[tree[rt].color]=true，返回；否则递归查询左右子树。统计所有颜色k ，若ans[k ]为真，则tot++，最后输出tot即可。

③ 更新[l , r ]区间的颜色为c 。若树根正好为该区间，则将根节点的颜色修改为c ，tree[rt].color=c ，返回；否则树根颜色下传（左右子树等于根的颜色，将根的颜色修改为0）；递归更新左右子树；返回时颜色统一（若左右子树颜色相同，则将树根的颜色也修改为该颜色）。

【本题秘诀】

• 查询时，遇到第1个颜色非0节点，标记后返回，否则递归查询左右子树；
• 更新时，将区间的颜色号修改为c ，在查找过程中颜色下传，回退时颜色统一。

【举个栗子】

① 创建线段树，树根的颜色为1（相当于懒标记），其他节点的颜色为0。

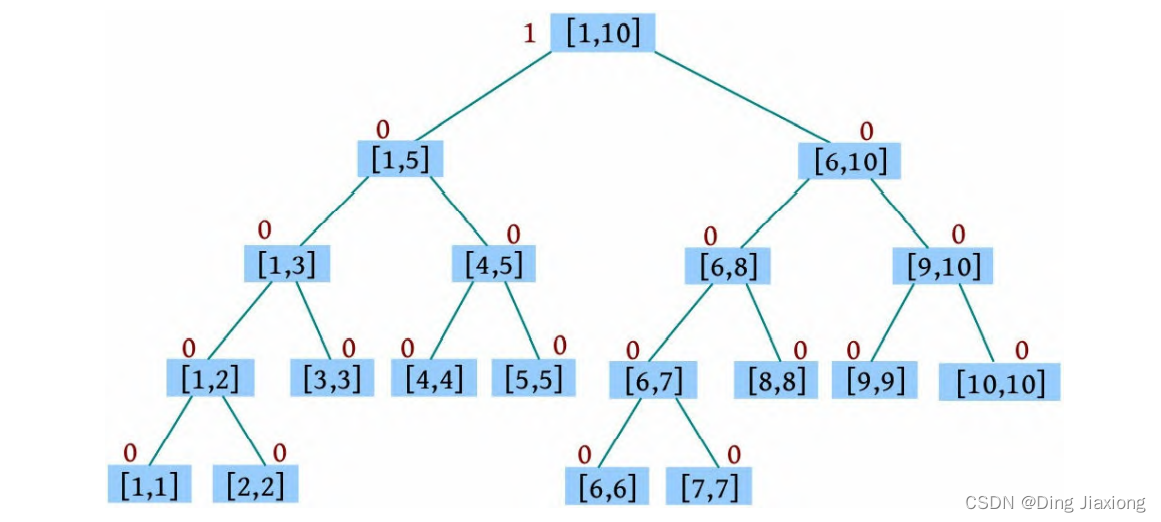
② P 1 2：统计1-2段的颜色数，因为树根[1, 10]为1号色，不为0，所以令ans[1]=true，返回；统计后1-2段的颜色数为1。

③ C 4 6 2：将4-6段涂2号色。首先搜索[4, 5]、[6, 6]区间，在搜索过程中若颜色不为0，则将其作为懒标记下传。将当前节点的懒标记下传给左右子节点，当前节点的颜色为0。

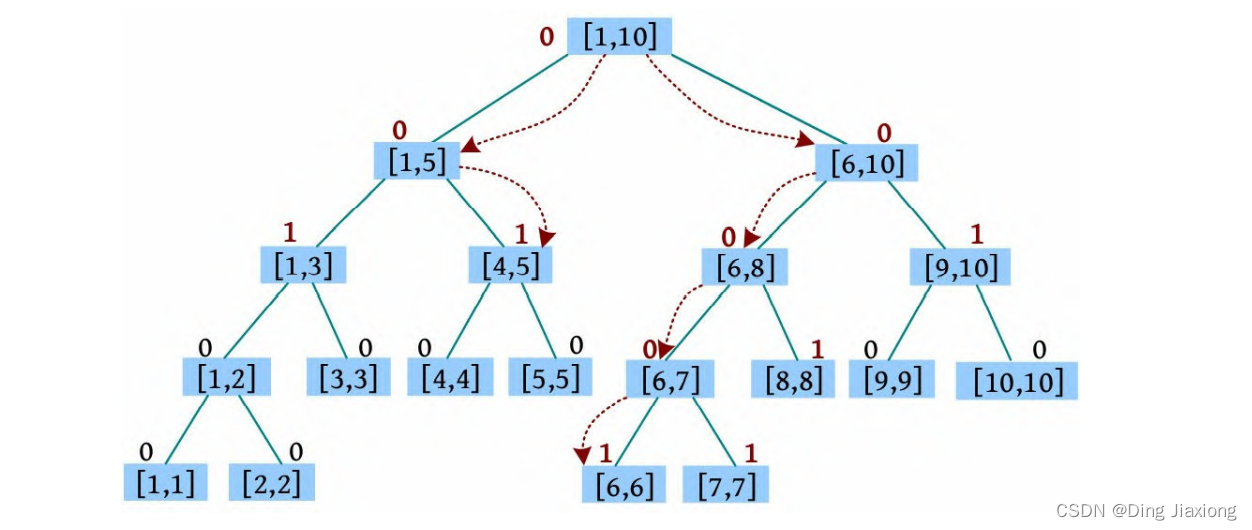
将[4, 5]、[6, 6]区间的颜色修改为2，然后返回，在返回过程中若当前节点的左右子树颜色相同，则当前节点的颜色和它们一致。

④ P 5 8：统计5-8段的颜色数，因为树根[1, 10]的颜色为0，所以递归查询左右子树，[4, 5]的颜色为2，令ans[2]=true，返回；[6, 6]的颜色为2，令ans[2]=true，返回；[7, 7]的颜色为1，令ans[1]=true，返回；[8, 8]的颜色为1，令ans[1]=true，返回。统计后5-8段的颜色数为2。

注意：查询时遇到第一个颜色不为0的节点才会返回。

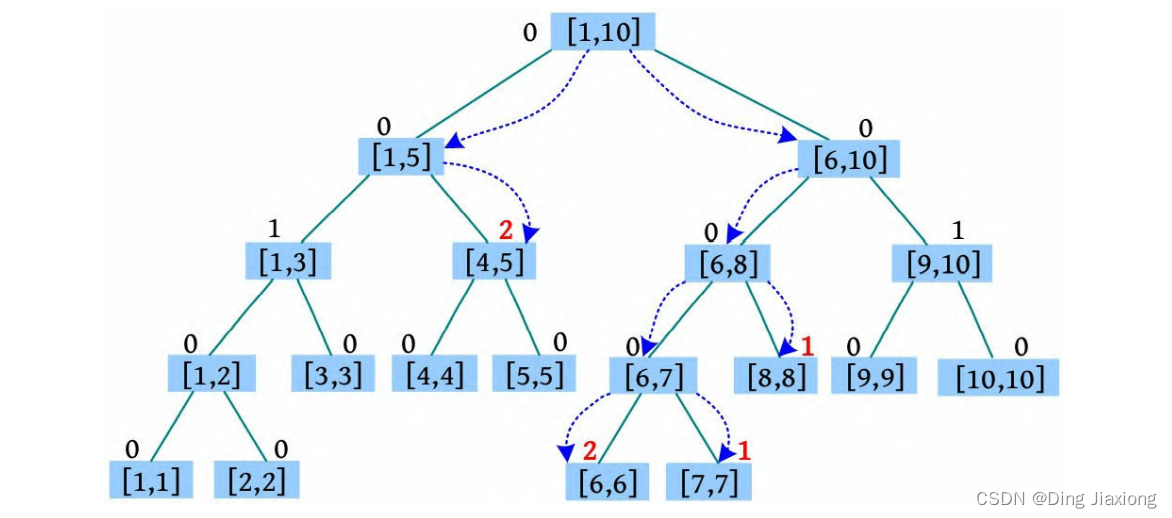
⑤ C 5 9 5：将5-9段涂1号色。首先搜索[5, 5]、[6, 8]、[9,9]区间。在搜索过程中若颜色不为0，则将其作为懒标记下传。

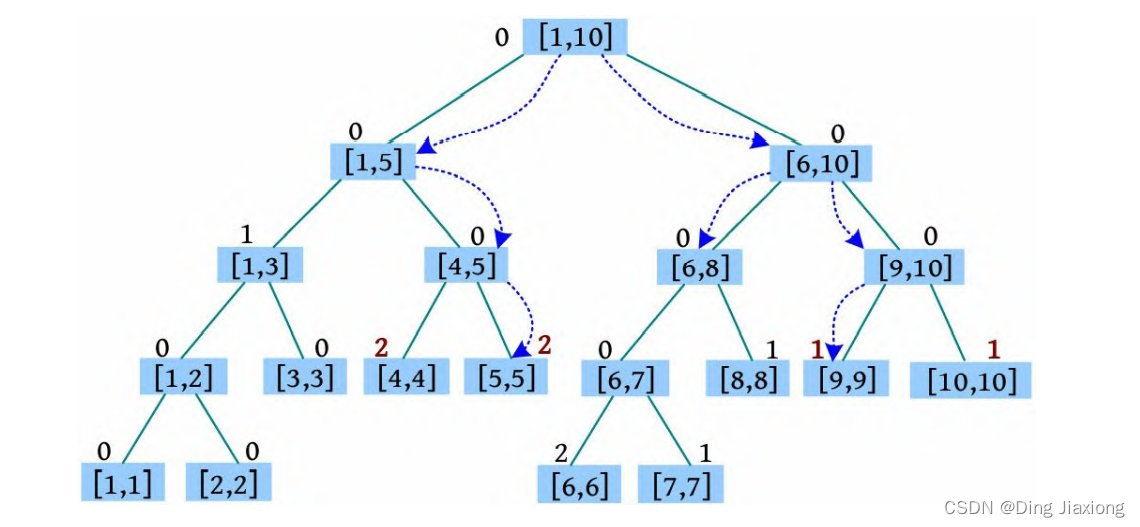
将[5, 5]、[6, 8]、[9, 9]区间的颜色修改为1，然后返回。返回时[9, 10]、[6, 10]区间左右子树的颜色相同，颜色修改与其左右子树一致，均为1。

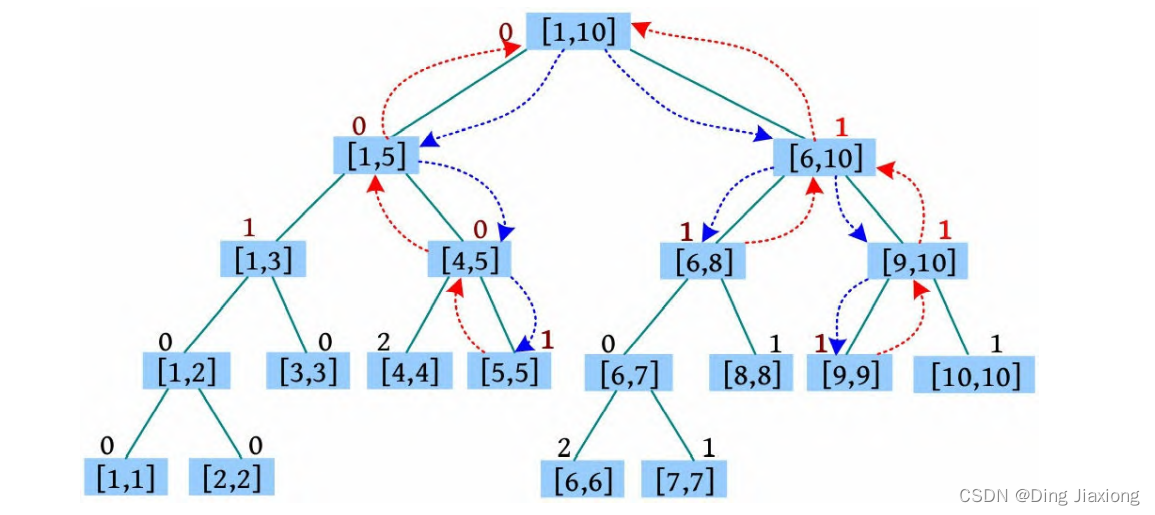
⑥ P 6 7：统计6-7段的颜色数，因为树根[1, 10]的颜色为0，所以递归查询右子树，[6, 10]的颜色为1，令ans[1]=true，返回。统计后6-7段的颜色数为1。

【算法实现】

#include<cstdio>
#include<cstring>
#define lc ((rt)<<1)
#define rc ((rt)<<1|1)
#define maxn 100010

int ans[50];

struct node{
    int l,r,color;
}tree[maxn*4];

void build(int rt,int l,int r){//创建线段树 
    tree[rt].l=l; tree[rt].r=r;
	if(rt!=1) tree[rt].color=0;
    if(l==r) return;
    int mid=(l+r)>>1;
    build(lc,l,mid); build(rc,mid+1,r);
}

void lift_up(int rt){//颜色统一 
    if(tree[lc].color==tree[rc].color)
		tree[rt].color=tree[lc].color;
}

void push_down(int rt){//颜色下传 
    if(tree[rt].color){
        tree[lc].color=tree[rc].color=tree[rt].color;
        tree[rt].color=0;
    }
}

void modify(int rt,int l,int r,int c){//修改 
    if (tree[rt].l==l&&tree[rt].r==r){
        tree[rt].color=c;
        return;
    }
    push_down(rt);
    int mid=(tree[rt].l+tree[rt].r)>>1;
    if(r<=mid) modify(lc,l,r,c);
    else if(l>mid) modify(rc,l,r,c);
	else {modify(lc,l,mid,c);modify(rc,mid+1,r,c);}
    lift_up(rt);
}

void query(int rt,int l,int r){//查询 
    if(tree[rt].color){
        ans[tree[rt].color]=true;
        return;
    }
    int mid=(tree[rt].l+tree[rt].r)>>1;;
    if(r<=mid) query(lc,l,r);
    else if(l>mid) query(rc,l,r);
    else {query(lc,l,mid);query(rc,mid+1,r);}
}

int main(){
	
    int n,t,o;
    scanf("%d%d%d",&n,&t,&o);
	
    tree[1].color=1;
    build(1,1,n);
    for(int i=0;i<o;i++){
        char ch;
        scanf("\n%c",&ch);
        int l,r;
        if(ch=='C'){
            int c;
            scanf("%d%d%d",&l,&r,&c);
            modify(1,l,r,c);
        }
        else{
            memset(ans,0,sizeof(ans));
            scanf("%d%d",&l,&r);
            query(1,l,r);
            int tot=0;
            for(int k=1;k<=t;k++)
				if(ans[k])
					tot++;
            printf("%d\n",tot);
        }
    }
	
    return 0;
}