目 录
摘 要 I
Abstract II
第一章 绪论 1
1.1课题研究背景和意义 1
1.2国内外研究现状 2
1.3本文的主要研究内容 4
第二章 混合馈能悬架系统的工作原理 5
2.1混合馈能悬架系统的设计理念 5
2.2馈能系统的原理 6
2.3馈能系统的类型 6
2.4混合馈能悬架系统结构选型 8
2.5本章小结 9
第三章 混合馈能悬架系统的设计 10
3.1直线电机的研究 10
3.1.1直线电机的结构 10
3.1.2直线电机的工作原理 10
3.2混合馈能悬架系统的结构设计 11
3.2.1传统悬架结构设计 11
3.2.2汽车悬架方案设计 12
3.3 小结 14
第四章 利用Adams/View进行混合馈能悬架建模仿真 15
4.1原始数据 15
4.2建立双横臂混合馈能悬架模型 15
4.2.1新建模型 16
4.2.2设置工作环境 17
4.2.3建立设计点 17
4.2.4建立模型 18
4.2.5添加运动副 20
4.2.6添加驱动 24
4.3建立测量参数 25
4.3.1创建主销后倾角的测量函数 26
4.3.2创建主销内倾角的测量函数 27
4.3.3创建车轮外倾角的测量函数 27
4.3.4创建车轮前束角的测量函数 27
第五章 利用Adams/View进行混合馈能悬架的优化 29
5.1优化目标 29
5.2主销后倾角优化 29
5.3主销内倾角优化 29
5.4前轮外倾角和前轮前束角优化 30
总 结 31
参考文献 32
致 谢 33
第三章 混合馈能悬架系统的设计
3.1直线电机的研究
在本次研究当中将会使用到直线电机作为混合馈能悬架系统的馈能减振器，为了能顺利的进行研究，现在将会对直线电机做一次详细的研究分析。了解其具体结构，以方便对其进行调整，与被动悬架更好的结合在一起。了解其具体性能，以便于更好的实现悬架的功能。
3.1.1直线电机的结构
直线电机式由旋转电机演变而成，其具体演变过程上文已经叙述过，这里就不在赘述了。直线电机的工作原理其实与旋转电机的工作原理相差不大，旋转电机由转子即永磁体旋转，由定子即磁感线圈切割磁感线产生电流。而直线电机也相差不大，直线电机是由对应转子的由永磁体做成的次级来回做直线式往复运动，而初级则是由硅钢片和三相线圈组成。
3.1.2直线电机的工作原理
当直线电机通入三相电流之后，会产生一个类似传统旋转电机通入三相电流产生的气隙磁场的行波磁场。传统旋转电机的气隙磁场是做圆周运动的，但是直线电机产生的行波磁场会沿直线电机做轴向运动。我们将直线电机产生的行波磁场的平移速度称为同步速度，其表达式为：
VS=2τf
其中τ为极距（m），f为频率（hz）
直线电机产生轴向的推力的原理和传统旋转电机产生转矩的原理相同，即，当次级的平移速度VS低于直线电机的同步速度时，就会产生滑移率，其表达式为：
S=(VS-V)/VS
每当出现滑移率时，次级就会切割行波磁场，因此产生轴向的电磁推力，驱动直线电机工作。直线电机的工作原理如图3-1.

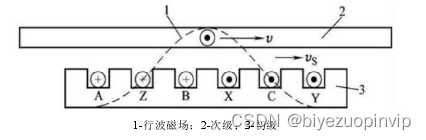
图3-1 直线电机的工作原理
根据直线电机的运动方向和推力方向，直线电机会分别处于电动机工作模式和发电机工作模式。当直线电机的运动方向和推力方向不同时，直线电机处于发电机工作模式，即馈能模式，将动能转化为电能储存起来；当直线电机的运动方向和推力方向相同时，直线电机处于发动机工作模式，将会主动调节悬架的参数，使悬架达到最佳工作状态。若是按照四个象限划分，当直线电机处于第一和第三象限时，直线电机处于发动机模式，主动调节悬架；当直线电机处于第二和第四象限时，直线电机处于馈能模式，将会收集汽车的振动能量转化为电能储存起来。
3.2混合馈能悬架系统的结构设计
这一小节将会进行本次研究相当重要的一个环节，就是进行混合馈能悬架系统的具体结构进行设计。因为这里面会将直线电机式馈能悬架与传统的麦弗逊式独立悬架结合在一起，所以难度比较大，属于本次研究的重大难点之一。在完成混合馈能悬架的设计之后，还需要进行建模，为了能更好的进行研究，我将先分别为直线电机馈能悬架部分和麦弗逊独立悬架部分建模，然后再考虑将两者结合在一起。
3.2.1传统悬架结构设计
现在开始麦弗逊式独立悬架部分的设计，首先需要确定的是悬架静挠度fc。悬架静挠度是指汽车满载静止时悬架上的载荷Fw与此时悬架刚度c之比。其表达式为：
fc=Fw/c
若想保证汽车有良好的行驶平顺性，必须正确选择悬架的静挠度。汽车的前后悬架静挠度应有略微的不同，对应不同用途的汽车，其前后悬架静挠度的差异也各有不同。一般来说，会希望后悬架的静挠度比前悬架的静挠度稍微小一点，因为这和车身的纵向角振动有关系。后悬架的静挠度比前悬架的静挠度小的话，会有利于防止车身产生较大的纵向角振动，会提高乘车的舒适性。但是乘用车顾及后排乘客的乘坐舒适感，有时候会选取后悬架的静挠度比前悬架的静挠度略高一点。
确认好悬架静挠度之后，需要确认悬架的动挠度fd。悬架的动挠度是指从满载静平衡位置开始悬架压缩到结构允许的最大变形时，车轮中心相对车身的垂直位移。为了避免车辆在坏路面上行驶时经常碰撞缓冲块，要求悬架动挠度应该要有足够大。一般来说，乘用车的悬架动挠度应在7_{9cm；客车的悬架动挠度应在5}8cm之间；火车的悬架动挠度应在6~9cm之间。

%% 状态空间方程矩阵A、B、F  LQG控制器矩阵Q、R、N
a1=(1/mhb+b^2/Ihp);
a2=(1/mhb-a*b/Ihp);
a3=(1/mhb+a^2/Ihp);
beta1=rou1*a3^2+rou2*a2^2;
beta2=rou1*a2*a3+rou2*a1*a2;
beta3=rou1*a2^2+rou2*a1^2;
%   A矩阵
A1=[-a1*Ksr a1*Ksr -a2*Ksf a2*Ksf;Ksr/mwr (-Ksr-Ktr)/mwr 0 0;-a2*Ksr a2*Ksr -a3*Ksf a3*Ksf;0 0 Ksf/mwf (-Ksf-Ktf)/mwf];%注意符号
A2=eye(4);
A=zeros(10);
A(1:4,5:8)=A1;A(5:8,1:4)=A2;
A(2,9)=Ktr/mwr;A(4,10)=Ktf/mwf;A(9,9)=-2*pi*f0;A(10,10)=-2*pi*f0;
Ab=A;%% 被动悬架
Ab1=[-a1*Csr a1*Csr -Csf*a2 a2*Csf
    1/mwr*Csr -1/mwr*Csr 0 0
    -a2*Csr a2*Csr -a3*Csf a3*Csf
    0 0 1/mwf*Csf -1/mwf*Csf];
Ab(1:4,1:4)=Ab1;%得到被动悬架矩阵
%   B矩阵
B1=[a2,a1;0,-1/mwr;a3,a2;-1/mwf,0];
B=zeros(10,2);B(1:4,:)=B1;
B=-B;
%   F矩阵
F=zeros(10,2);
F(9,1)=2*pi*sqrt(G0*uc);F(10,2)=2*pi*sqrt(G0*uc);
%   Q矩阵
Q1=[q4+Ksr^2*beta3 -q4-Ksr^2*beta3 Ksf*Ksr*beta2 -Ksf*Ksr*beta2;-q4-Ksr^2*beta3 q3+q4+Ksr^2*beta3 -Ksf*Ksr*beta2 Ksf*Ksr*beta2;Ksf*Ksr*beta2 -Ksf*Ksr*beta2 q2+Ksf^2*beta1 -q2-Ksf^2*beta1;-Ksf*Ksr*beta2 Ksf*Ksr*beta2 -q2-Ksf^2*beta1 q1+q2+Ksf^2*beta1];
Q=zeros(10);
Q(5:8,5:8)=Q1;
Q(6,9)=-q3;Q(8,10)=-q1;Q(9,6)=-q3;Q(9,9)=q3;Q(10,8)=-q1;Q(10,10)=q1;
%   R矩阵
R=[beta1 beta2;beta2 beta3];
%   N矩阵
N1=[Ksr*beta2 Ksr*beta3;-Ksr*beta2 -Ksr*beta3;Ksf*beta1 Ksf*beta2;-Ksf*beta1 -Ksf*beta2];
N=zeros(10,2);
N(5:8,:)=N1;
[K,S,E]=lqr(A,B,Q,R,N);      %K最优控制反馈增益矩阵，S为黎卡提方程解，E为系统闭环特征根值：调用 matlab 线性二次最优控制器设计函数[K,S,E]=LQR(A,B,Q,R,N);