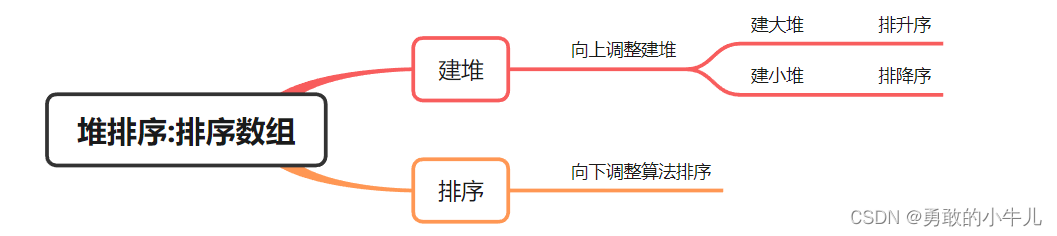
思维导图:
目录
一,堆排序的概念
二,堆排序的实现
2.1将数组变成堆
2.2堆有序化
二,全部代码
一,堆排序的概念
百度百科的解释如下:堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
也就是说,堆排序是一种利用堆这种数据结构来对数据进行排序的算法。
二,堆排序的实现
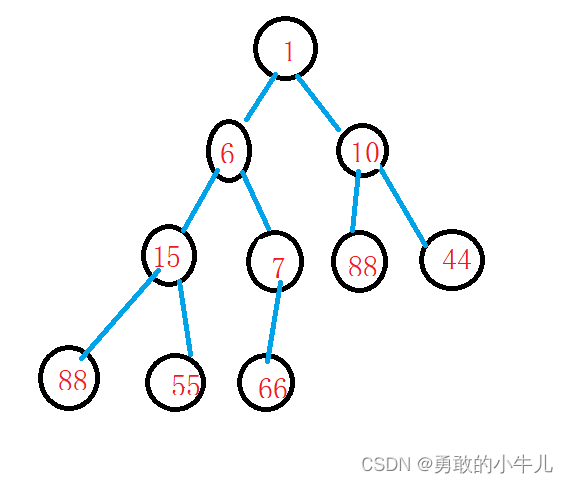
想要使用堆排序,那我们就要有堆。但是堆是什么呢?堆实际上就是数组。所以我们可以对数组进行堆排序。比如数组:a[10] = { 55,1,88,15,66,10,44,88,7,6 }。如果用满二叉树的结构来表示,那就是:
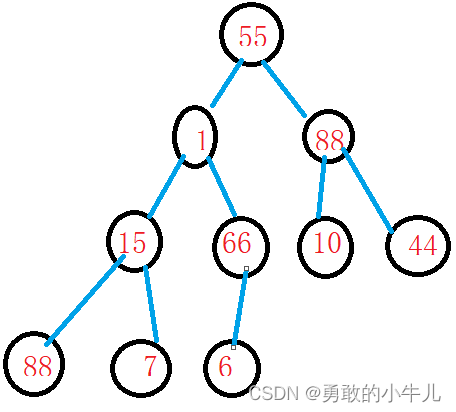
这样子的。但是,这是一个堆吗?其实很容易的看出这不是一个堆。因为如果它是一个堆的话,那它不是大堆就是一个小堆。小堆就要满足父节点要比子节点要小,大堆就要满足父节点要比子节点要大。但是这个堆是一个条件都不满足,所以它不是一个堆。
2.1将数组变成堆
我们现在想要让一个数组变成堆,比如数组:a[10] = { 55,1,88,15,66,10,44,88,7,6 }。
堆排序的前提是什么?有堆!我们要对数组进行堆排序的话还需要插入数据建堆吗?不需要了。但是我们要对数组的数据进行调整来让它变成一个大堆或小堆。那我们该怎么做到调整数组的数据来建立一个规规矩矩的大堆或小堆呢?答案是利用向上调整算法。
向上调整算法代码:
void AdjustUp(int* a, int n)//向上调整算法创建小堆
{
assert(a);
int child = n;
int parent = (child-1)/2;//寻找子节点的父节点
while (child > 0)
{
if (a[child] < a[parent])//利用循化不断调整子节点与父节点之间的关系
{
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}这个代码该怎么运行呢?
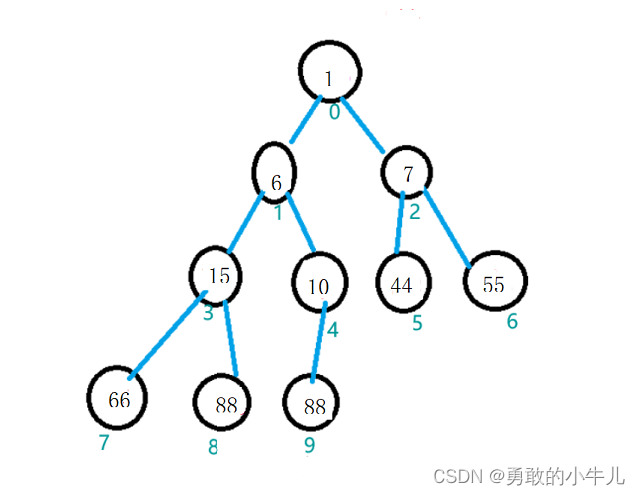
以这个不规矩的堆为例:

#绿色数字是下标#
当我们使用AdjustUp时:AdjustUp(a,9)。那我们要调整的就是下标为:9->4->1->0这一支。
因为我们要建立的是小堆,所以调整以后我们的堆就会变成:
可以看到,画上蓝色圈的这一支就被调整完毕了。但是这个堆还不是一个规规矩矩地堆。
所以为了让这个堆变成一个规规矩矩的堆,我们就这样使用堆排序:
for (int i = 0;i < sizeof(a) / sizeof(a[0]);i++) { AdjustUp(a, i);//每次插入数据都向上调整。 }经过这个操作以后,我们的堆就会变成:
这就是一个名正言顺的小堆了。但是它仍然不是有序的(升序或降序)
2.2堆有序化
通过上述向上调整的操作以后,可以看到这个数组已经被调整成一个小堆了。但是它仍然不是有序的。这就没有实现排序的功能。所以为了将这个堆变得有序,我们就要通过另外两个操作:1.交换根节点与最后一个节点 2.向下调整建堆。
1.交换根节点与最后一个节点
代码:
void swap(int* p1, int* p2)//交换函数swap
{
int temp = *p1;
*p1 = *p2;
*p2 = temp;
}2.向下调整函数
代码:
void AdjustDown(int* a, int n, int parent)
{
assert(a);
int child = 2 * parent + 1;//默认孩子节点是左节点
while (child < n)
{
if (a[child] < a[parent])
{
if (child + 1 < n && a[child] > a[child + 1])//如果右节点小于左节点那就将左节点变成右节点
{
child++;
}
swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}但是和向上调整建堆一样,这个代码只能调整一支。并且不能排序。但是通过下面的操作,我们就能排序了。
代码:
int end = sizeof(a) / sizeof(a[0]) - 1;
while (end > 0)
{
swap(&a[0], &a[end]);//交换首尾两个数
AdjustDown(a, end, 0);//向下调整实现降序的堆排序
end--;//每次都要调整交换最后一个叶子节点的位置
}经过向上调整以后,我们的堆是这样的:
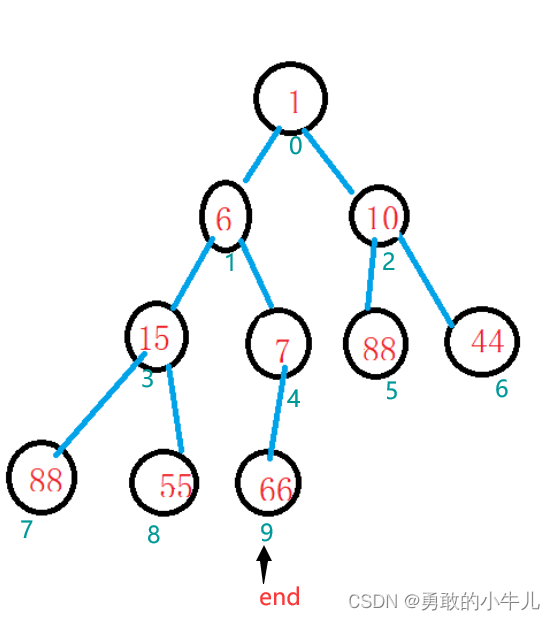
经过第一个swap调整以后变成这样:
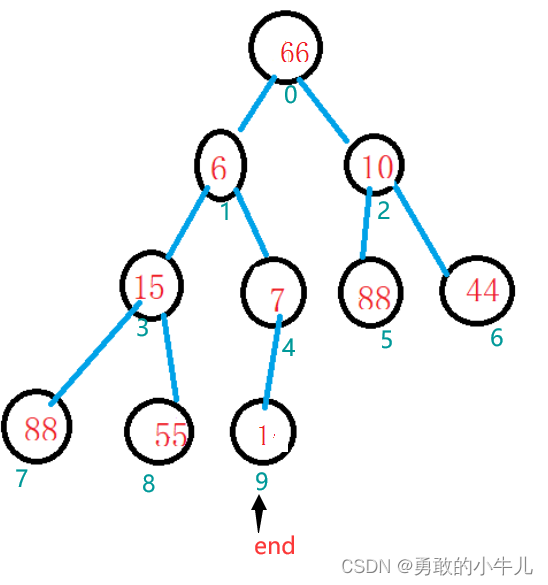
这一步操作直接将最小的值放在了最后一个位置。
然后执行向下调整:
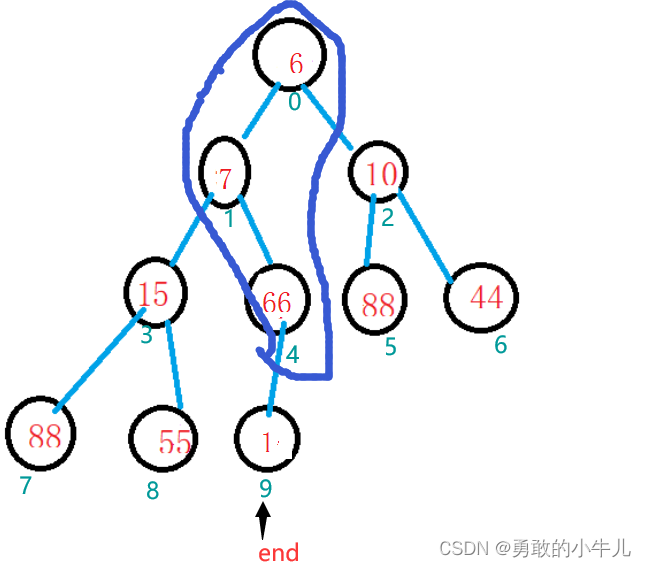
向下调整,调整了画圈的那一支。这个操作的目的就是将次小的数据放在根节点处。
然后end--,交换根节点与end指向的节点的值。将次小的数放在倒数第二的位置:

然后再交换,以此类推将每一个小数据放在后面就会将数组变成一个降序的数组:
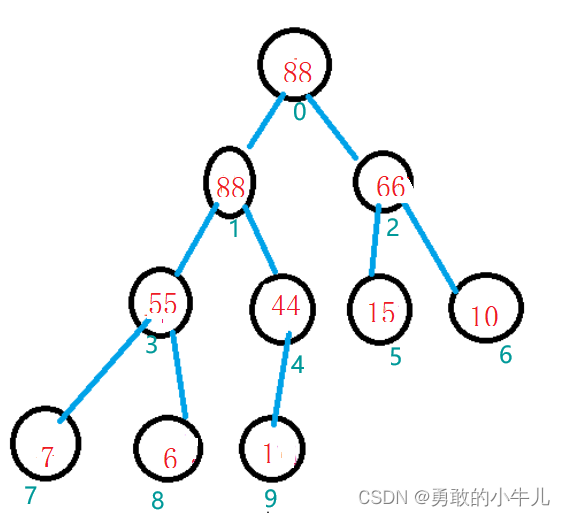
假如你想要得到一个升序的数组怎么办呢?只要一个操作。把建立的小堆改成大堆就行了。
代码:
先建立大堆:
void AdjustUp(int* a, int n)//向上调整算法创建大堆
{
assert(a);
int child = n;
int parent = (child-1)/2;//寻找子节点的父节点
while (child > 0)
{
if (a[child] > a[parent])//利用循化不断调整子节点与父节点之间的关系
{
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}大堆:

向下调整排序变成升序:
void AdjustDown(int* a, int n, int parent)
{
assert(a);
int child = 2 * parent + 1;
while (child < n)
{
if (a[child] >a[parent])
{
if (child + 1 < n && a[child] < a[child + 1])
{
child++;
}
swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}while (end > 0)
{
swap(&a[0], &a[end]);//交换首尾两个数
AdjustDown(a, end, 0);//向下调整实现降序的堆排序
end--;//每次都要调整交换最后一个叶子节点的位置
}排序后:
#注意#:
这里建大堆变成建小堆的操作的改变就是改变一下父节点与子节点的交换条件----子节点小于父节点时交换节点改为子节点大于父节点时交换节点。排序堆也是将节点的交换条件改变。
#总结# :
在写完两个排序后可以总结到:
1.要排升序就要建立大堆。
2.要排降序就要建小堆。
二,全部代码
排升序:
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
void swap(int* p1, int* p2)//交换函数swap
{
int temp = *p1;
*p1 = *p2;
*p2 = temp;
}
void AdjustUp(int* a, int n)//向上调整算法创建小堆
{
assert(a);
int child = n;
int parent = (child-1)/2;//寻找子节点的父节点
while (child > 0)
{
if (a[child] > a[parent])//利用循化不断调整子节点与父节点之间的关系
{
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void AdjustDown(int* a, int n, int parent)
{
assert(a);
int child = 2 * parent + 1;
while (child < n)
{
if (a[child] >a[parent])
{
if (child + 1 < n && a[child] < a[child + 1])
{
child++;
}
swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
int main()
{
int a[10] = { 55,1,88,15,66,10,44,88,7,6 };
for (int i = 0;i < sizeof(a) / sizeof(a[0]);i++)
{
AdjustUp(a, i);//向上调整建堆
}
int end = sizeof(a) / sizeof(a[0]) - 1;
while (end > 0)
{
swap(&a[0], &a[end]);//交换首尾两个数
AdjustDown(a, end, 0);//向下调整实现降序的堆排序
end--;//每次都要调整交换最后一个叶子节点的位置
}
return 0;
}排降序:
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
void swap(int* p1, int* p2)//交换函数swap
{
int temp = *p1;
*p1 = *p2;
*p2 = temp;
}
void AdjustUp(int* a, int n)//向上调整算法创建小堆
{
assert(a);
int child = n;
int parent = (child-1)/2;//寻找子节点的父节点
while (child > 0)
{
if (a[child] < a[parent])//利用循化不断调整子节点与父节点之间的关系
{
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void AdjustDown(int* a, int n, int parent)
{
assert(a);
int child = 2 * parent + 1;
while (child < n)
{
if (a[child] <a[parent])
{
if (child + 1 < n && a[child] > a[child + 1])
{
child++;
}
swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
int main()
{
int a[10] = { 55,1,88,15,66,10,44,88,7,6 };
for (int i = 0;i < sizeof(a) / sizeof(a[0]);i++)
{
AdjustUp(a, i);//向上调整建堆
}
int end = sizeof(a) / sizeof(a[0]) - 1;
while (end > 0)
{
swap(&a[0], &a[end]);//交换首尾两个数
AdjustDown(a, end, 0);//向下调整实现降序的堆排序
end--;//每次都要调整交换最后一个叶子节点的位置
}
return 0;
}