文章目录
- 前言
- 一、贝叶斯算法简介
- 二、贝叶斯算法的数学原理
- 1. 条件概率
- 2. 全概率公式
- 3. 贝叶斯公式
- 4. 朴素贝叶斯分类器
- 5. 高斯朴素贝叶斯分类器和伯努利朴素贝叶斯分类器
- 三、Python实现朴素贝叶斯分类
- 总结
前言
贝叶斯公式是我们高中就耳熟能详的统计概率定理,贝叶斯公式给我带来的震撼就是竟然有人能通过已知去预测未知,有种说不出的神秘感!可能在世俗的理念中,这种未来的预测是十分荒谬不合乎逻辑的,但贝叶斯却用一个数学模型囊括了用先验概率求解后验概率分布的推理过程,真的不可思议!
一、贝叶斯算法简介
贝叶斯算法是一种基于贝叶斯定理的统计学习方法,用于分类、预测和推理等问题。它的基本思想是利用先验概率和样本数据来计算后验概率,从而进行分类或预测。
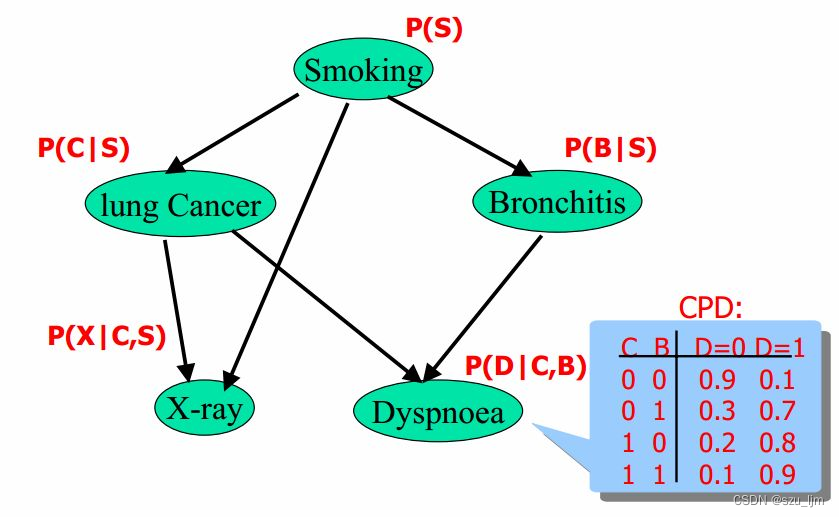
具体来说,贝叶斯算法假设分类结果是由多个特征共同决定的,并且这些特征之间是相互独立的。通过对已知分类的训练数据进行统计分析,可以计算出每个特征对于每个分类的条件概率,即给定某个分类的情况下,某个特征出现的概率。这些条件概率和每个分类的先验概率(即在没有任何数据的情况下,每个分类出现的概率)一起使用,就可以通过贝叶斯定理计算出每个分类的后验概率,即在给定特征的情况下,每个分类出现的概率。最终,根据后验概率大小进行分类或预测。
贝叶斯算法有两种常用的实现方式:朴素贝叶斯和贝叶斯网络。朴素贝叶斯算法假设所有特征之间是相互独立的,因此可以简化计算过程。贝叶斯网络则是一种图模型,用于描述变量之间的关系,可以处理特征之间存在依赖关系的情况。
贝叶斯算法在文本分类、垃圾邮件过滤、推荐系统等领域得到了广泛应用,它不仅具有较高的分类准确率,而且还可以处理多分类和高维数据等问题。
二、贝叶斯算法的数学原理
1. 条件概率

条件概率就是后验概率,它想表达的就是事件A在另一个事件B已经发生的条件下发生的概率,我们用
P
(
A
∣
B
)
P(A|B)
P(A∣B) 来表达条件概率
P
(
A
∣
B
)
=
P
(
A
B
)
P
(
B
)
P(A|B) = \frac{P(AB)}{P(B)}
P(A∣B)=P(B)P(AB)

条件概率公式描述了后验概率是可以通过先验概率来进行推导的,即但我们知道事件A发生的概率和事件A事件B一起发生的概率,我们可以反向推导事件A在另一个事件B已经发生的条件下发生的概率
2. 全概率公式
光有条件概率还不够,如果在事件集中我们如何继续应用条件概率的思想去解决一些问题,这时候就需要全概率计算。如果事件 B 1 , B 2 , B 3 , ⋯ , B n B_{1}, B_{2}, B_{3}, \cdots, B_{n} B1,B2,B3,⋯,Bn 构成一个完备事件组 B B B 且都有正概率,那么我们可以用全概率公式来表达事件 A A A 发生的概率
P ( A ) = ∑ i = 1 n P ( A ∣ B i ) P ( B i ) P(A)= \sum_{i=1}^{n} P(A|B_{i})P(B_{i}) P(A)=i=1∑nP(A∣Bi)P(Bi)
全概率公式将条件概率和先验概率结合起来,揭示了条件概率在事件集中逆向转换过程,算是对单一事件条件概率的一种延伸
3. 贝叶斯公式

贝叶斯研究了一个非常有意思的东西,如果通过一个条件概率转化计算出另一个互补的条件概率,那我们就可以预测一些很有意思的事情,于是贝叶斯定理就诞生了,贝叶斯学派的思想可以概括为先验概率+数据=后验概率。贝叶斯公式可以表达为事件A在事件B发生的条件下的发生概率比上事件A发生的概率等于事件B在事件A发生的条件下的发生概率比上事件B发生的概率
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B) = \frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
在机器学习中,我们把这事件A和事件B等价于特征和标签,于是就可以得到贝叶斯算法的基本定理,几乎所有的贝叶斯算法都是基于下面的原理进行展开优化的
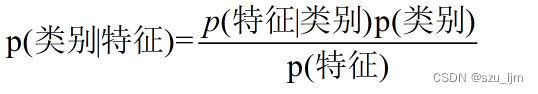
4. 朴素贝叶斯分类器
在现实生活中,想要对某件事的发生做一个预测,一定会考虑到很多因素特征,朴素贝叶斯的出现就帮助我们简化很多特征因素间繁琐的关系考量。朴素贝叶斯算法是一种基于贝叶斯定理和特征条件独立假设的分类算法。其核心思想是利用已知类别的样本数据集,通过计算特征之间的条件概率,来预测新样本所属的类别。类别标签 y y y 在几个特征因素的条件概率可以表达为
P ( y ∣ x 1 , x 2 , . . . , x n ) = P ( y ) P ( x 1 , x 2 , . . . , x n ∣ y ) P ( x 1 , x 2 , . . . , x n ) P(y|x_1, x_2, ..., x_n) = \frac{P(y)P(x_1, x_2, ..., x_n|y)}{P(x_1, x_2, ..., x_n)} P(y∣x1,x2,...,xn)=P(x1,x2,...,xn)P(y)P(x1,x2,...,xn∣y)
其中, y y y 表示类别, x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn 表示特征向量, P ( y ∣ x 1 , x 2 , . . . , x n ) P(y|x_1, x_2, ..., x_n) P(y∣x1,x2,...,xn) 表示在给定特征向量 x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn 的条件下,样本属于类别 y y y 的概率。
朴素贝叶斯算法假设所有的特征之间都是独立的,也就是说我们在考虑一件事情的几个影响因素时,将每个因素看作是互不影响的独立个体。由于这一假设,模型包含的条件概率的数量大为减少,朴素贝叶斯法的学习与预测大为简化。根据独立性假设,可以将 P ( x 1 , x 2 , . . . , x n ∣ y ) P(x_1, x_2, ..., x_n|y) P(x1,x2,...,xn∣y) 展开为每个特征在给定类别下的条件概率的乘积:
P ( x 1 , x 2 , . . . , x n ∣ y ) = ∏ i = 1 n P ( x i ∣ y ) P(x_1, x_2, ..., x_n|y) = \prod_{i=1}^{n} P(x_i | y) P(x1,x2,...,xn∣y)=i=1∏nP(xi∣y)
其中, P ( y ) P(y) P(y) 表示类别 y y y 在样本中的先验概率, P ( x i ∣ y ) P(x_i|y) P(xi∣y) 表示在给定类别 y y y 的条件下,特征 x i x_i xi 出现的概率, P ( x 1 , x 2 , . . . , x n ) P(x_1, x_2, ..., x_n) P(x1,x2,...,xn) 表示特征向量 x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn 出现的概率。
P ( y ∣ x 1 , x 2 , . . . , x n ) = P ( y ) ∏ i = 1 n P ( x i ∣ y ) P ( x 1 , x 2 , . . . , x n ) P(y|x_1, x_2, ..., x_n) = \frac{P(y) \prod\limits_{i=1}^{n}P(x_i|y)}{P(x_1, x_2, ..., x_n)} P(y∣x1,x2,...,xn)=P(x1,x2,...,xn)P(y)i=1∏nP(xi∣y)
在实际应用中,由于 P ( x 1 , x 2 , . . . , x n ) P(x_1, x_2, ..., x_n) P(x1,x2,...,xn) 对于所有类别都是相同的,因此可以省略分母,仅考虑分子部分,选择具有最大后验概率的类别作为预测结果,最后我们会得到 y ^ \hat{y} y^ 表示预测的类别
y ^ = arg max y P ( y ) ∏ i = 1 n P ( x i ∣ y ) \hat{y} = \arg\max_{y} P(y) \prod_{i=1}^{n} P(x_i | y) y^=argymaxP(y)i=1∏nP(xi∣y)
5. 高斯朴素贝叶斯分类器和伯努利朴素贝叶斯分类器
高斯朴素贝叶斯算法是朴素贝叶斯算法的一种常见形式,适用于特征变量为连续值的情况。在高斯朴素贝叶斯算法中,假设每个类别下的特征变量服从高斯分布,因此可以用高斯分布的概率密度函数来计算条件概率。最终预测的类别 y ^ \hat{y} y^ 的表达式为
y ^ = arg max y P ( y ) ∏ i = 1 n 1 2 π σ y , i 2 exp ( − ( x i − μ y , i ) 2 2 σ y , i 2 ) \hat{y} = \arg\max_{y} P(y) \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi\sigma_{y,i}^2}} \exp\left(-\frac{(x_i - \mu_{y,i})^2}{2\sigma_{y,i}^2}\right) y^=argymaxP(y)i=1∏n2πσy,i21exp(−2σy,i2(xi−μy,i)2)
伯努利朴素贝叶斯算法是朴素贝叶斯算法的一种常见形式,适用于特征变量为二元变量的情况。在伯努利朴素贝叶斯算法中,假设每个特征变量都是二元变量,即只有两种取值,如 0 和 1。因此,每个特征变量的条件概率只有两种取值,分别对应于特征变量取值为 0 和 1 的情况。最终预测的类别 y ^ \hat{y} y^ 的表达式为
y ^ = arg max y P ( y ) ∏ i = 1 n P i ∣ y x i ( 1 − P i ∣ y ) 1 − x i \hat{y} = \arg\max_{y} P(y) \prod_{i=1}^{n} P_{i|y}^{x_i} (1 - P_{i|y})^{1-x_i} y^=argymaxP(y)i=1∏nPi∣yxi(1−Pi∣y)1−xi
三、Python实现朴素贝叶斯分类
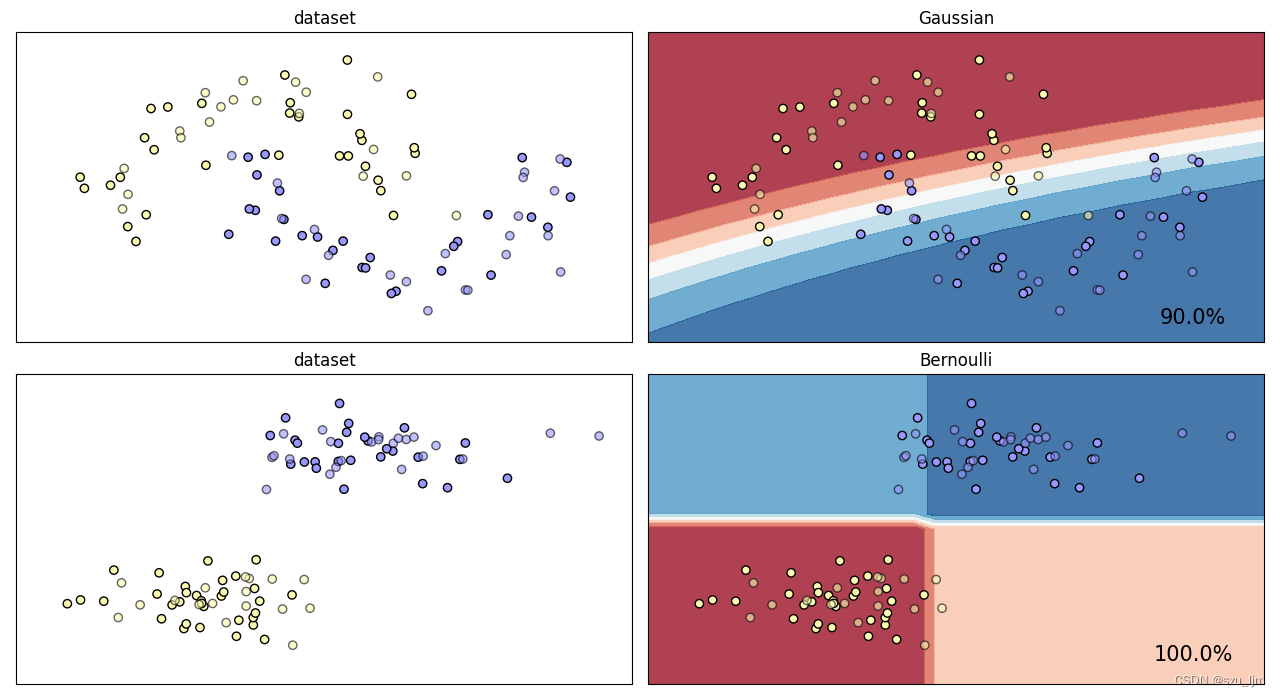
Python实现朴素贝叶斯分类的思路,首先导包,这次我们选择月亮数据集和块状数据集,选择高斯朴素贝叶斯分类器和伯努利朴素贝叶斯分类器,接着实例化对象并创建画布,然后定义一个画图函数,首先标准化数据集并画好网格,接着画散点图并创建子图,最后训练模型,并把返回预测值,拉长进行决策边界等高线可视化
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_moons, make_circles, make_blobs
from sklearn.naive_bayes import GaussianNB, MultinomialNB, BernoulliNB, ComplementNB
# 模型的名字
names = ["Gaussian", "Bernoulli"]
# 创建我们的模型对象
classifiers = [GaussianNB(), BernoulliNB()]
# 创建数据集
datasets = [ make_moons(noise=0.2, random_state=0),make_blobs(centers=2, random_state=2),]
# 创建画布
figure = plt.figure(figsize=(12, 8))
def plot_clf(NB_clf, dataset, name, i):
X, y = dataset
# 标准化数据集
X = StandardScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.4, random_state=42)
# 对画布画网格线
x1_min, x1_max = X[:, 0].min() - .5, X[:, 0].max() + .5
x2_min, x2_max = X[:, 1].min() - .5, X[:, 1].max() + .5
array1, array2 = np.meshgrid(np.arange(x1_min, x1_max, 0.2),
np.arange(x2_min, x2_max, 0.2))
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#fafab0', '#9898ff'])
i += 1
ax = plt.subplot(len(dataset), 2, i)
ax.set_title("dataset")
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train,
cmap=cm_bright, edgecolors='k')
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test,
cmap=cm_bright, alpha=0.6, edgecolors='k')
ax.set_xlim(array1.min(), array1.max())
ax.set_ylim(array2.min(), array2.max())
ax.set_xticks(())
ax.set_yticks(())
i += 1
ax = plt.subplot(len(dataset), 2, i)
clf = NB_clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
Z = clf.predict_proba(np.c_[array1.ravel(), array2.ravel()])[:, 1]
Z = Z.reshape(array1.shape)
ax.contourf(array1, array2, Z, cmap=cm, alpha=.8)
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright,
edgecolors='k')
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright,
edgecolors='k', alpha=0.6)
ax.set_xlim(array1.min(), array1.max())
ax.set_ylim(array2.min(), array2.max())
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(name)
ax.text(array1.max() - .3, array2.min() + .3, ('{:.1f}%'.format(score * 100)),
size=15, horizontalalignment='right')
for i in range(2):
plot_clf(classifiers[i], datasets[i], names[i], 2*i)
plt.tight_layout()
plt.show()
总结
以上就是贝叶斯算法学习笔记的全部内容,本篇笔记简单介绍了贝叶斯算法的数学原理以及python实现的程序思路。朴素贝叶斯算法有很多优势,比如具有良好的可解释性,可以给出每个特征对于分类的影响程度,便于理解和解释;计算速度快,适合处理大规模数据集和高维数据;对于噪声数据和缺失数据有很好的鲁棒性;在处理文本分类和情感分析等自然语言处理任务上表现优异。总的来说,贝叶斯算法的意义依旧不可估量。