前言：最近准备复习一下深度学习的基础知识，开个专栏记录自己的学习笔记

各种SGD和Adam优化器整理

基本概念

优化：最大化或最小化目标函数，具体指最小化代价函数或损失函数

损失函数 J(θ)=f(hθ(x)，y)，hθ(x)是由参数θ构成的网络输出

梯度下降：为了使得损失函数达到最小所采取的方法或策略
具体步骤：

• 计算梯度，这里的梯度只损失函数在参数θ的梯度
• 更新参数：根据计算的损失函数梯度，求更新后的参数（θ=θ-α * g）学习率 * 梯度

SGD（stochastic gradient descent）随机梯度下降

每次更新时用1个样本
优点：
缺点：

• 缺点在于收敛速度慢，
• 可能在鞍点处震荡
• 学习率难以选择

BGD（Batch Gradient Descent）批量梯度下降

每一次迭代时使用所有样本来进行梯度的更新
优点：

• 全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向

缺点：

• 需要遍历全部样本才更新一次，耗费时间长
• 由于是由全部的样本求的平均损失函数的梯度进行计算，有些sample可能对参数更新不起作用

MBGD（Mini-batch Gradient Descent) 小批量梯度下降

每次迭代我们从所有样本的训练集中依次按固定批量样本进行梯度更新，直到遍历所有样本

MBSGD（Mini-batch Gradient Descent) 小批量随机梯度下降

每次迭代我们从所有样本的训练集（已经打乱样本的顺序）中随机抽出一小批量(mini-batch)样本进行梯度更新

SGD with momentum 带动量的随机梯度更新

公式

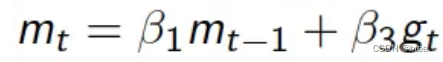
即按照动量来更新参数（而不是梯度）
动量为两部分构成，其中一部分由上一时刻的动量决定，另一部分由当前梯度决定，β一般取0.9
因此动量可以看成有了惯性的梯度

优点：
在相同学习率和相同更新时间内，Momentum加速能行驶更多路程，为越过不那么好的极小值点提供可能性

SGD with NAG（Nesterov accelerated gradient）

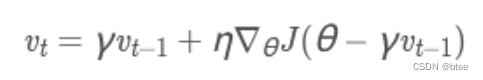
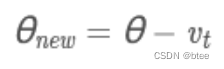
这里的γ是衰减率=β，η是学习率=α
原理：根据动量进一步推导而来，带动量的参数更新另一部分由当前梯度决定，这里不是由当前梯度决定，而是下一步梯度决定，即假设第一部分动量作用后更新梯度决定

AdaGrad 自适应学习率梯度下降法

SGD 、SGD-M、SGD-NAG都是固定学习率去学习参数
但是对于更新不频繁的参数，我们希望学习率大以学到更多知识，对于更新频繁的参数，我们希望学习率小以保持稳定
二阶动量的表示：

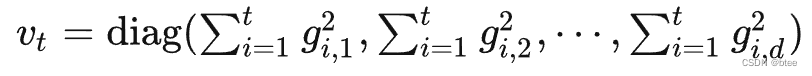
Vt是个对角矩阵，代表不同维度上迄今为止所有梯度的平方和
AdaGrad用全局学习率除以这个数，作为学习率的动态更新。

更新频繁的参数，二阶动量的对应分量大

AdaDelta

Adam

AdamW

RMSProp

Nadam