数据结构初阶 —— 二叉树链式结构

news2025/1/10 3:16:40

一，二叉树链式结构

二，二叉树的遍历（四种）

前序遍历

中序遍历

后序遍历

层序遍历

三，二叉树接口

四，试题

一，二叉树链式结构

普通二叉树的增删查改，意义不大；
普通二叉树+搜索树规则，增删查改才有价值；

//二叉树链式结构
typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;
}BTNode;

//创建节点
BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("BuyNode");
		exit(-1);
	}
	node->_data = x;
	node->_left = node->_right = NULL;
	return node;
}

//自定义二叉树
BTNode* CreatBinaryTree()
{
	BTNode* nodeA = BuyNode('A');
	BTNode* nodeB = BuyNode('B');
	BTNode* nodeC = BuyNode('C');
	BTNode* nodeD = BuyNode('D');
	BTNode* nodeE = BuyNode('E');
	BTNode* nodeF = BuyNode('F');
	nodeA->_left = nodeB;
	nodeA->_right = nodeC;
	nodeB->_left = nodeD;
	nodeC->_left = nodeE;
	nodeC->_right = nodeF;
	return nodeA;
}

二，二叉树的遍历（四种）

前序遍历，根 $\rightarrow$ 左子树 $\rightarrow$ 右子树；
中序遍历，左子树 $\rightarrow$ 根 $\rightarrow$ 右子树；
后序遍历，左子树 $\rightarrow$ 右子树 $\rightarrow$ 根；
层序遍历，一层一层遍历；

注：深度优先遍历（前序、中序、后序），广度优先遍历（层序）；

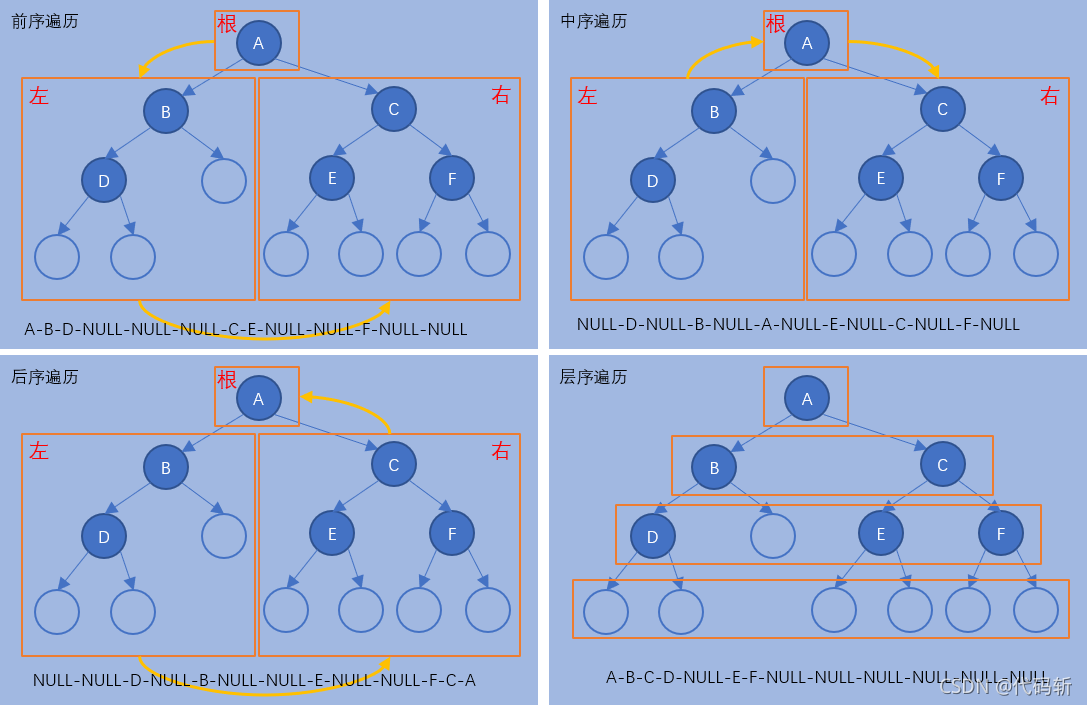
前序遍历

//前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
		return;
	printf("%c ", root->_data);
	PreOrder(root->_left);
	PreOrder(root->_right);
}

中序遍历

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
		return;
	InOrder(root->_left);
	printf("%c ", root->_data);
	InOrder(root->_right);
}

后序遍历

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
		return;
	PostOrder(root->_left);
	PostOrder(root->_right);
	printf("%c ", root->_data);
}

层序遍历

//层序遍历-利用队列
//一个节点出列，入列其子节点
typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode
{
    QDataType data;
    struct QueueNode* next;
}QueueNode;
typedef struct Queue
{
    QueueNode* phead;
    QueueNode* ptail;   
}

void LevelOrder(BTNode* root)
{
    Queue q;
    QueueInit(&q);
    if(root)
        QueuePush(&q, root);
    while(!QueueEmpty(&q))
    {
        BTNode* front = QueueFront(&q);
        QueuePop(&q);
        printf("%c ", front->val);
        if(front->left)
            QueuePush(&q, front->left);
        if(front->right)
            QueuePush(&q, front->right);
    }
    printf("\n");
    QueueDestroy(&q);
}

三，二叉树接口

//求二叉树节点个数-递归
//方法一，全局变量或static
int size = 0; 
void BinaryTreeSize(BTNode* root)
{
	if (root)
		size++;
	else
		return;
	BinaryTreeSize(root->_left);
	BinaryTreeSize(root->_right);
}

//方法二，局部变量-传址
void BinaryTreeSize(BTNode* root, int* psize)
{
	if (root)
		(*psize)++;
	else
		return;
	BinaryTreeSize(root->_left, psize);
	BinaryTreeSize(root->_right, psize);
}

//方法三，返回值
int BinaryTreeSize(BTNode* root)
{
	if (root)
		return 1 + BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right);
	else
		return 0;
}

//求二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->_left == NULL && root->_right == NULL)
		return 1;
	return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

//求二叉树第k层节点个数
//当前树第K层节点个数 = 其左子树的第K-1层节点个数 + 其右子树的第K-1层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}

//求二叉树深度
//当前树深度 = max(左子树深度， 右子树深度) + 1；
int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
		return 0;
	int leftDepth = BinaryTreeDepth(root->_left);
	int rightDepth = BinaryTreeDepth(root->_right);
	return leftDepth > rightDepth ? (1 + leftDepth) : (1 + rightDepth);
}

//二叉树查找值为x的节点
//先当前节点查找，没有，在去左子树查找，没有，在取右子树查找
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->_data == x)
		return root;

	BTNode* retLeft = BinaryTreeFind(root->_left, x);
	if (retLeft)
		return retLeft;

	BTNode* retRight = BinaryTreeFind(root->_right, x);
	if (retRight)
		return retRight;

	return NULL;
}

//二叉树的销毁
void BinaryTreeDestory(BTNode* root)
{
    if(root==NULL)
        return;
    BinaryTreeDestory(root->left);
    BinaryTreeDestory(root->right);
    free(root);
}

//判断二叉树是否是完全二叉树
//利用层序，空也入列，完全二叉树非空是连续的
bool BinaryTreeComplete(BTNode* root)
{
    Queue q;
    QueueInit(&q);
    if(root)
        QueuePush(&q, root);
    while(!QueueEmpty(&q))
    {
        BTNode* front = QueueFront(&q);
        QueuePop(&q);
        if(front == NULL)
            break;
        QueuePush(&q, front->left);
        QueuePush(&q, front->right);
    }
    while(!QueueEmpty(&q))
    {
        BTNode* front = QueueFront(&q);
        QueuePop(&q);
        if(front)
        {
            QueueDestroy(&q);
            return false; 
        }
    }
    QueueDestroy(&q);
    return true;
}