一.什么是前缀和算法
通俗来讲,前缀和算法就是使用一个新数组来储存原数组中前n-1个元素的和(如果新数组的当前元素的下标为n,计算当前元素的值为原数组中从0到n-1下标数组元素的和),可能这样讲起来有点抽象,我们举一个例子对其进行说明:给定一个数组nums[],我们创建一个大小为nums.length+1的求和数组sums[],对sum[]数组进行遍历:sum[i]=nums[0]+nums[1]+...+nums[i-1](相当于nums[i-1]+sum[n-1]),比如存在int[]nums={1,2,3,4},对应的前缀和数组的值为sum={0,1,3,6,10}
二.前缀和算法相对于滑动窗口具有哪些不可替代的优势及前缀和算法对算法题目的优化策略
我们在前面讲述的前缀和算法,可能很多小伙伴对其的特点也有所察觉:发现其与我们上一节讲到的滑动窗口有些类似,我们结合下面这道题目,讲讲前缀和算法对于如下这种题目而言,具有怎样的解题优势

对于滑动窗口一般的解题思路如下:如果当前窗口的元素大于预期条件的元素时,我们将窗口的左指针向右移动;如果当前窗口的元素小于预期条件的元素时,我们将窗口的右指针向右移动,扩大窗口,但是对于上面的题目中,测试用例中存在负数的情况,那么对于窗口中出现了负数这种情况,我们是该将窗口右移直到满足条件还是将窗口左移直到剔除这个负数呢?这明显超出了我们之前规定的对于使用滑动窗口的条件,这也就是滑动窗口的局限性,而根据我们对于上文中对前缀和算法的描述,前缀和算法并不规定其中的元素一定要是正数或者负数,我们只是将其中的元素进行相加,而前缀和算法对于解决这种题目可谓大显身手。
除此之外,我们讲一下前缀和算法的应用相对于我们使用暴力解法具有怎样的优化:如果不创建一个新的数组来存储前n个元素的和,那么此时我们每次求和时,都需要从头到尾将元素和全部求一遍,对于一维数组,时间复杂度达到了O(n),但是如果我们将前面元素和进行存储,每次求和只需要调用我=我们前缀和数组中的元素,时间复杂度只有O(1),大大降低了时间复杂度;同理,对于二维数组而言,他可以将O(n^2)的时间复杂度降至O(1).
三.前缀和算法的模板代码
对于前缀和算法,一般存在一维的前缀和与二维的前缀和这样两种不同的算法模板,关于前缀和算法的模板,我们使用preSum来计算数组的前缀和,preSum[i]代表着前i个前i-1个数组元素的和;对于二维数组,preSum[i][j]则代表着行为 0到i-1,列为0-j-1元素的和
一维前缀和模板
如下是一维前缀和算法的模板代码:

public int[] preSum(int[] nums) {
int[] preSum = new int[nums.length+1];
for (int i = 1; i < =nums.length; ++i) {
preSum[i] = preSum[i - 1] + nums[i-1];
}
return preSum;
}二维前缀和模板
如下是二维前缀和的算法模板:对于二维的前缀和模板,是对一维前缀和模板的扩展,但在本质上是完全一致的,我们来描述有关二维数组的前缀和的模板:

我们给出这样一个图示: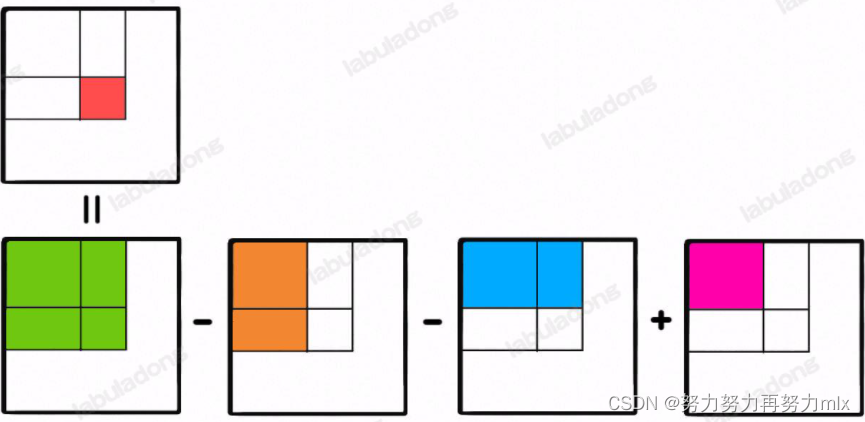
对于二维数组的前缀和而言,表达式可以表述为这样:
每一个二维数组中的单位元素,相等于绿-澄-蓝+粉,我们同样给出一个二维数组,presum[nums.length+1][nums[0].length+1],presum[n][n]则代表0-n-1行,0-n-1列的数据总和 、
其模板表达式如下:
class NumMatrix {
// 定义:preSum[i][j] 记录 matrix 中子矩阵 [0, 0, i-1, j-1] 的元素和
private int[][] preSum;
public NumMatrix(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
if (m == 0 || n == 0) return;
// 构造前缀和矩阵
preSum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// 计算每个矩阵 [0, 0, i, j] 的元素和
preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
}
}
}
// 计算子矩阵 [x1, y1, x2, y2] 的元素和
public int sumRegion(int x1, int y1, int x2, int y2) {
// 目标矩阵之和由四个相邻矩阵运算获得
return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
}
}除了完全的一维和二维的前缀和算法之外,前缀和算法的题目通常会与hash等数据结构组合出题
四.关于前缀和算法的经典题目练习
1.区域和检索 - 数组不可变力扣
力扣题目描述

解题思路
这是一个完全意义上的前缀和算法的题目,或者说这是一个书写前缀和算法模板的题目,对于这道题,我们直接使用我们前面使用的前缀和算法的模板即可:创建nums.length+1长度的presum[],对于presum[n],存储的是前n-1个元素的和,每次求和时直接使用presum中的元素即可。
实例代码
我们给出实例代码:
class Solution {
public int subarraySum(int[] nums, int k) {
//单纯使用前缀和,无法判别从哪里进行区分,这时我们需要将符合条件的数值直接存入map,再次需要时直接拿来使用即可
int count=0;//记录最终的结果
int pre=0;//记录前缀和
//创建map
HashMap<Integer,Integer>map=new HashMap<>();
//如果是pre-target=0,代表从0开始刚好满足条件要求
map.put(0,1);
for(int i=0;i<nums.length;++i){
pre+=nums[i];
if(map.containsKey(pre-k)){
count+=map.get(pre-k);
}
//将当前pre加入
map.put(pre,map.getOrDefault(pre,0)+1);
}
return count;
}
}class NumArray {
//本题使用前缀和算法,将使劲复杂度从O(n)降至O(1)
private int[]preNums;
public NumArray(int[] nums) {
preNums=new int[nums.length+1];
//循环时创建前缀和
for(int i=1;i<preNums.length;++i){
preNums[i]=preNums[i-1]+nums[i-1];
}
}
public int sumRange(int left, int right) {
return preNums[right+1]-preNums[left];
}
}2.和为 k 的子数组 力扣
题目描述

解题思路
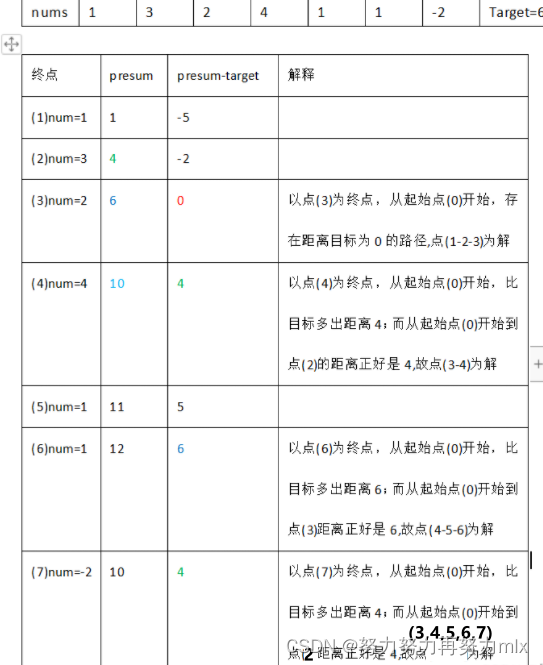
这道题就是对我们一维数组前缀和算法的扩展了,它不仅仅使用简单的前缀和数组进行存储数组的前缀和,他同样需要使用hash表进行元素的记录和存储,这是一道前缀和数组和哈希表进行融合的题目,具体的解题思路如下:我们对于这道题目而言,难点在于对于简单的前缀和数组而言,我们无法判断从哪个地方进行断开(无法判断从那个地方作为起点,哪个地方作为终点是符合条件的),因为我们在此基础上使用哈希表,哈希表中存储的是当前元素为基准的前缀和与target之间的差距,如果差距为0(恰好满足)或者当前差距等于其前面元素的前缀和(如果前面元素的前缀和为4,此时前缀和-target=4 :前缀和比我们需要的和的值大4,刚好与前面的值进行抵消),这种也是符合条件的。
图示如下:
实例代码
我们给出实例代码
class Solution {
public int subarraySum(int[] nums, int k) {
//单纯使用前缀和,无法判别从哪里进行区分,这时我们需要将符合条件的数值直接存入map,再次需要时直接拿来使用即可
int count=0;//记录最终的结果
int pre=0;//记录前缀和
//创建map
HashMap<Integer,Integer>map=new HashMap<>();
//如果是pre-target=0,代表从0开始刚好满足条件要求
map.put(0,1);
for(int i=0;i<nums.length;++i){
pre+=nums[i];
if(map.containsKey(pre-k)){
count+=map.get(pre-k);
}
//将当前pre加入
map.put(pre,map.getOrDefault(pre,0)+1);
}
return count;
}
}3.二维子矩阵的和力扣
题目描述

解题思路
这道题正是我们上面讲述的关于二维数组求前缀和的典型例题,我们在上面模板的基础上进行思路的讲解:对于红框内的元素和,等于绿框元素-蓝框-红框+黑框(其中蓝框和红框中也有黑框的部分,但是被颜色覆盖了),在此之前,我们首先要将元素进行初始化,初始化的过程相当于对元素进行分割的逆过程:单位元素加上两边的元素再减去重复的元素


实例代码
class NumMatrix {
//创建二维的数组和
private int[][]preNums;
public NumMatrix(int[][] matrix) {
preNums=new int[matrix.length+1][matrix[0].length+1];
//创建并遍历
for(int i=1;i<preNums.length;++i){
for(int j=1;j<preNums[0].length;++j){
preNums[i][j]=preNums[i][j-1]+preNums[i-1][j]-preNums[i-1][j-1]+matrix[i-1][j-1];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
return preNums[row2+1][col2+1]-preNums[row2+1][col1]-preNums[row1][col2+1]+preNums[row1][col1];
}
}4.除自身以外数组的乘积力扣
题目描述

解题思路
这道题目的解题思路相对而言比较巧妙,它将前缀和拓展为前缀积,而除了本身元素之外的其他元素的和,则恰好符合前缀积中premul[i]*lastmul[i]的定义,所以直接定义前缀后缀积进行元素的相乘即可
实例代码
class Solution {
public int[] productExceptSelf(int[] nums) {
//解题思路:通过前缀积和后缀积进行相乘,最终的结果就是除了nums[i]之外的相乘结果,需要注意的是:需要对前后缀积的含义进行一定的改变
//定义前缀积
int[]pre=new int[nums.length];
//定义后缀积
int[]last=new int[nums.length];
//初始化并相乘
pre[0]=1;
for(int i=1;i<nums.length;++i){
pre[i]=nums[i-1]*pre[i-1];
}
last[nums.length-1]=1;
for(int i=nums.length-2;i>=0;--i){
last[i]=last[i+1]*nums[i+1];
}
int[]res=new int[nums.length];
//进行最后的结果返回
for(int i=0;i<nums.length;++i){
res[i]=pre[i]*last[i];
}
return res;
}
}