题解 . 洛谷题单之动态规划的引入

news2024/11/20 23:35:48

前置知识：

数字三角形问题：动态规划之数字三角形模型_如何何何的博客-CSDN博客

01背包问题：动态规划之01背包模型_如何何何的博客-CSDN博客

完全背包问题：动态规划之完全背包模型_如何何何的博客-CSDN博客

多重背包问题：动态规划之多重背包模型_如何何何的博客-CSDN博客

题1. 数字三角形 Number Triangles

P1216 [USACO1.5][IOI1994]数字三角形 Number Triangles - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：

数字三角形裸题。

AC代码如下：

#include<iostream>
#include<cstring>
using namespace std;

const int N = 510;
int g[N][N], f[N][N];//三角形，以每个点为终点的路径的最大值
int n;

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++)//读入地图（其实可以在读入的时候就处理，这里将读入和处理分开了）
        for (int j = 1; j <= i; j++)
            cin >> g[i][j];

    memset(f, -0x3f, sizeof f);//初始化
    f[1][1] = g[1][1];

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= i; j++) {
            if (j - 1 >= 1)f[i][j] = max(f[i][j], f[i - 1][j - 1] + g[i][j]);//如果左上角未越界
            if (j < n)f[i][j] = max(f[i][j], f[i - 1][j] + g[i][j]);//如果右上角未越界
        }

    int res = -0x3f3f3f3f;//在最后一行中找最大值
    for (int i = 1; i <= n; i++)res = max(res, f[n][i]);

    cout << res;
    return 0;
}

题2. 采药：

P1048 [NOIP2005 普及组] 采药 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：

01背包裸题。

AC代码如下：

#include<iostream>
using namespace std;
const int N=1010;
int f[N];
int main(){
    int t,n;//读入时间和草药数量
    int v,w;//时间和价值
    cin>>t>>n;
    for(int i=1;i<=n;i++){//枚举前n株草药
        cin>>v>>w;//读入当前草药的时间和价值
        for(int j=t;j>=v;j--)//滚动数组
            f[j]=max(f[j],f[j-v]+w);
    }
    cout<<f[t];
    return 0;
}

题3. 挖地雷:

P2196 [NOIP1996 提高组] 挖地雷 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：

数据范围较小，可以使用dfs；

dp做法：最长上升子序列模型，f[i]表示以 i 点为结尾的路径的最大值；

由题可知图为拓扑图，每一层所有点的状态都是由上一层的点更新得到，故按层次枚举即可；

由题可知编号小的点连向编号大的点，不存在编号大的点连向编号小的点，故根据编号从小到大枚举即可；

记录每个点的前驱即可得到路径。

AC代码如下：

#include<iostream>
#include<vector>
using namespace std;
const int N=25;
int p[N];//地雷数
int f[N];//状态
int pre[N][N];//每个点的前驱
int path[N];//前驱路径 

int main(){
	int n;
	cin>>n;
	
	//地雷数 
	for(int i=1;i<=n;i++)cin>>p[i];
	
	//每个点的前驱 
	for(int i=1;i<=n;i++)
		for(int j=i+1;j<=n;j++)
			cin>>pre[j][i];
	
	for(int i=1;i<=n;i++){
		f[i]=p[i];
		path[i]=i;
		
		for(int j=1;j<i;j++)
			//如果i点状态被更新 
			if(pre[i][j]) 
				if(f[i]<f[j]+p[i]){f[i]=f[j]+p[i];path[i]=j;}
	}
	
	int res=0,k=0;
	for(int i=1;i<=n;i++)
		if(res<f[i]){res=f[i];k=i;}
	
	vector<int>v;
	bool flag=false;
	while(1){
		if(path[k]==k)flag=true;
		v.push_back(k);
		k=path[k];
		if(flag)break;
	} 
	
	for(int i=v.size()-1;i>=0;i--)cout<<v[i]<<" ";
	cout<<endl<<res;
	return 0;
}

题4. 滑雪：

P1434 [SHOI2002] 滑雪 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：

类似数字三角形模型，f[i][j] 表示 ( i , j ) 点的最大长度；

f[i][j] 由上下左右四个方向转移得到，并且可知高度低的点一定由高度高的点转移得到；

故可以将所有点按照高度进行排序，然后两重循环进行状态更新，第一重从大到小枚举所有点，第二重枚举所有较高的点来做更新；

注意：相同高度的不能滑过去。

AC代码如下：

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1010;
int g[N][N];
int f[N][N]; 
int n,m;
//点的坐标及其高度 
struct pp{
	int x,y,h;
}p[N*N];
int dx[]={1,0,-1,0},dy[]={0,1,0,-1}; 

bool cmp(struct pp a,struct pp b){
	return a.h>b.h;
}

int main(){
	cin>>n>>m;
	int k=0;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++){
			cin>>g[i][j];
			p[k].x=i,p[k].y=j,p[k++].h=g[i][j];
		}
	//从大到小排 
	sort(p,p+n*m,cmp);
		
	
	for(int i=0;i<n*m;i++){//从大到小枚举所有点 
		f[p[i].x][p[i].y]=1;
		//枚举所有较高的 
		for(int j=0;j<i;j++){
			//相同高度 
			if(p[j].h==p[i].h)continue;
			//该点是否可用 
			bool flag=false;
			for(int m=0;m<4;m++)
				if(p[j].x+dx[m]==p[i].x&&p[j].y+dy[m]==p[i].y)flag=true;
				
			if(flag)
				f[p[i].x][p[i].y]=max(f[p[j].x][p[j].y]+1,f[p[i].x][p[i].y]);
		}
	}
	
	int res=0;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)res=max(res,f[i][j]);
		
	cout<<res;
	return 0; 
}

题5 . 最大食物链计数：

P4017 最大食物链计数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：

f[i] 表示以 i 号点结尾的食物链数量，f[i] 由 i 点上一层的点转移得到（上一层点的状态之和）；

食物网为拓扑图，但无法直接按层次遍历，存在如下反例，直接按层次遍历答案为1：

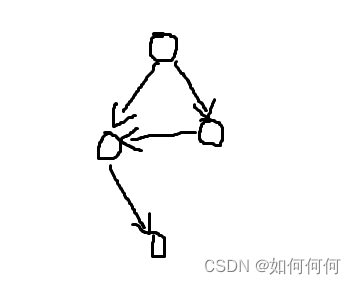
暂时未写，后续补充。

题6. 最大子段和：

P1115 最大子段和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：

双指针，DP；

DP解法：

f [i] 表示以 i 号位置的数字结尾的最大子段和；

状态转移方程：f[i] = max ( f[i-1] + a[i] , a[i] )。

AC代码如下：

#include<iostream>
using namespace std;
const int N=2*1e5+10;
int f[N];

int main(){
	int n;
	cin>>n;
	
	int res=-0x3f3f3f3f;
	for(int i=0;i<n;i++){
		cin>>f[i];
		f[i]=max(f[i],f[i-1]+f[i]);
		res=max(res,f[i]);
	}
	
	cout<<res;
}

题7. 5倍经验日：

P1802 5 倍经验日 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：

01背包问题；

f[i][j] 表示打 第 i 个人，且有 j 瓶药的最大经验；

状态转移：f[i][j] = max( f[i-1][j] + l[i]，f[i-1][j-1] + w[i] )。

AC代码如下：

#include<iostream>
using namespace std;
const int N=1010;
int w[N],s1[N],s2[N];
long long f[N][N];

int main(){
    int n,m;
    cin>>n>>m;
    
    for(int i=1;i<=n;i++)
        cin>>s1[i]>>s2[i]>>w[i];
    
    for(int i=1;i<=n;i++)
        for(int j=0;j<=m;j++){
            f[i][j]=f[i-1][j]+s1[i];
            if(j>=w[i])f[i][j]=max(f[i][j],f[i-1][j-w[i]]+s2[i]);
        }
        
    cout<<f[n][m]*5;
    
}

题8. 过河卒：

P1002 [NOIP2002 普及组] 过河卒 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：

f[i][j] 表示走到 ( i , j ) 的路径数量；

状态转移：只能从左上角走到，f[i][j] = f[i-1][j] + f[i][j-1]。

AC代码如下：

#include<iostream>
using namespace std;
int n,m,x1,y1;
const int N=25;
long long f[N][N];
int main(){
    f[0][1]=1;
    cin>>n>>m>>x1>>y1;
    n++,m++,x1++,y1++;   
int dx[] = { -2, -1, 1, 2, 2, 1, -1 ,- 2,0 }, dy[] = {  1,2, 2, 1, -1,- 2,- 2, -1,0 };
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            int st=0;
            for(int u=0;u<9;u++)
                if(i==x1+dx[u]&&j==y1+dy[u])st=1;
            if(st==1)f[i][j]=0;
            else f[i][j]=f[i-1][j]+f[i][j-1];
        }
    f[1][1]=0;
    cout<<f[n][m];
    return 0;
}

题9. 装箱问题：

P1049 [NOIP2001 普及组] 装箱问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：

01背包裸题。

AC代码如下：

#include<iostream>
using namespace std;
const int N=20010;
int f[N];
int n,V;

int main(){
	cin>>V>>n;
	for(int i=1;i<=n;i++){
		int v;
		cin>>v;
		for(int j=V;j>=v;j--)
			f[j]=max(f[j],f[j-v]+v);
	}
	cout<<V-f[V];
	return 0;
}

题10. 疯狂的采药：

P1616 疯狂的采药 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：

完全背包问题裸题。

AC代码如下：

#include<iostream>
using namespace std;

const int N=1e7+10;
long long f[N];

int main(){
    int n,m;
    cin>>n>>m;//时间与数量
    
    int t,s;
    for(int i=1;i<=m;i++){
        cin>>t>>s;
        
        for(int j=t;j<=n;j++)
            f[j]=max(f[j],f[j-t]+s);
    }
    
    cout<<f[n];
    
    return 0;

}

题11. 小A点菜：

P1164 小A点菜 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：

01背包问题：

f[i][j] 表示只考虑前 i 道菜，花掉 j 元的方案数；

状态转移方程 f[i][j] = f[i-1][j] + f[i-1][j-w[i]]。

AC代码如下:

#include<iostream>
using namespace std;
const int N=1010;
int f[N][N];
int a[N];
int n,m;//n种菜m元钱
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    
    f[0][0]=1;
        
    for(int i=1;i<=n;i++)
        for(int j=0;j<=m;j++){
            if(j>=a[i])f[i][j]=f[i-1][j]+f[i-1][j-a[i]];
            else f[i][j]=f[i-1][j];
        }
        
    cout<<f[n][m];
    return 0;
}

题12. 摆花：

P1077 [NOIP2012 普及组] 摆花 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：

多重背包问题；

f[i][j] 表示只选前 i 种花，共有 j 盆花的选法；

状态转移方程：f[i][j] += ( f[i-1][j] + f[i-1][j-1] + f[i-1][j-2] + …… + f[[i-1][j-a[i]] ) 。

AC代码如下：

#include<iostream>
using namespace std;
const int N=110,mod=1e6+7;
int f[N][N];

int main(){
	int n,m;
	cin>>n>>m;
	
	f[0][0]=1;
	for(int i=1;i<=n;i++){//前i种花 
		int a;
		cin>>a;
		for(int j=0;j<=m;j++){//总共j盆花 
			for(int k=0;k<=a&&k<=j;k++){//选k盆i种花
			    f[i][j]+=f[i-1][j-k];	 
			    f[i][j]%=mod;
			}
		}
	}
	
	cout<<f[n][m];	
	return 0;
}

题12. 线段：

P3842 [TJOI2007]线段 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：

f[i][0] 表示走完第 i 行的线段后停在线段左端的最短步数，f[i][1] 表示走完第 i 行的线段后停在线段右端的最短步数；

假设 a[i][0] 表示第 i 行的线段左端点，a[i][1] 表示第 i 行的线段右端点；

状态转移：第 i 行的端点状态由第 i-1 行的左端点或右端点转移得到，一共两种情况，取最小值即可。

AC代码如下：

#include<iostream>
#include<cmath>
using namespace std;
const int N=1e4*2;
int f[N][2],g[N][2];

int main(){
	int n;
	cin>>n;
	
	f[0][0]=f[0][1]=0;//初始0步 
	g[0][0]=g[0][1]=1;//初始位置为1 
	
	for(int i=1;i<=n;i++){
		cin>>g[i][0]>>g[i][1];
		
		f[i][0]=min(
					//上一层左端点转移得到
					f[i-1][0] + 1 + (g[i][1]-g[i][0]) + abs(g[i-1][0]-g[i][1]), 
					//上一层右端点转移得到
					f[i-1][1] + 1 + (g[i][1]-g[i][0]) + abs(g[i-1][1]-g[i][1])
					);
		f[i][1]=min(
					//上一层左端点转移得到 
					f[i-1][0] + 1 + (g[i][1]-g[i][0]) + abs(g[i-1][0]-g[i][0]),
					//上一层右端点转移得到 
					f[i-1][1] + 1 + (g[i][1]-g[i][0]) + abs(g[i-1][1]-g[i][0])
					);
		
	}
	
	int res;
	res=min( f[n][0]+abs(g[n][0]-n),f[n][1]+abs(g[n][1]-n) );
	cout<<res-1;
	return 0; 
}

题13. 金明的预算方案：

P1064 [NOIP2006 提高组] 金明的预算方案 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

暂时未写，后续补充。

题14. kkksc03考前临时抱佛脚：

P2392 kkksc03考前临时抱佛脚 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：

搜索、DP；

DP解法：

01 背包问题，对于每个题目有写与不写两种情况；

对于每个科目，尽量平均分为两部分；

将做题时间看做体积和价值，即求一半容量下能装下的物品的最大价值是多少；

AC代码如下：

#include<iostream>
#include<cstring>>
using namespace std;
const int N=25;
int f[N][N*60];
int a[N];
int b[N];

int main(){
	//每组题目的数量 
	for(int i=0;i<4;i++)cin>>a[i];
	
	int res=0;
	//4组物品 
	for(int i=0;i<4;i++){
		//总体积为v 
		int v=0;
		for(int j=1;j<=a[i];j++){cin>>b[j];v+=b[j];}
		
		//01背包
		memset(f,0,sizeof f);
		
		for(int j=1;j<=a[i];j++)
			for(int k=0;k<=v;k++){
				f[j][k]=f[j-1][k];
				if(k>=b[j])f[j][k]=max(f[j][k],f[j-1][k-b[j]]+b[j]);
			} 
		res+=(v-f[a[i]][v/2]);
		
	}
	
	cout<<res;
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/562211.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

两种蚁狮群优化(Ant Lion Optimizer, ALO)实现及仿真实验——附代码

两种蚁狮群优化(Ant Lion Optimizer, ALO)实现及仿真实验——附代码

目录 蚁狮群优化算法介绍&#xff1a; 总结概括&#xff1a; ALO算法设计&#xff1a; 1.觅食的蚂蚁随机行走 2.设置陷阱 3.设置陷阱诱捕蚂蚁 4.捕获猎物重建洞穴 多目标MOALO算法 两种蚁狮算法求解效果 (1) ALO (2) MOALO Matlab代码分享&#xff1a; 蚁狮群优化算…
阅读更多...
CleanMyMac X4.13.5中文版Mac电脑优化软件

CleanMyMac X4.13.5中文版Mac电脑优化软件

CleanMyMac X4.13.5是一款Mac电脑优化软件&#xff0c;旨在提高Mac电脑的性能、稳定性和安全性。它可扫描您的Mac电脑&#xff0c;并删除不需要的文件、清理缓存、卸载不必要的应用程序、优化启动项、检测并删除恶意软件等。此外&#xff0c;它还可以帮助您管理您的文件&#x…
阅读更多...
Python库 pdf2docx 轻松将PDF转换成docx

Python库 pdf2docx 轻松将PDF转换成docx

前言&#xff1a; 可将 PDF 转换成 docx 文件的 Python 库。该项目通过 PyMuPDF 库提取 PDF 文件中的数据&#xff0c;然后采用 python-docx 库解析内容的布局、段落、图片、表格等&#xff0c;最后自动生成 docx 文件。 pdf2docx功能 解析和创建页面布局 页边距章节和分栏 (目…
阅读更多...
腾讯云-服务违规封禁提醒解决

腾讯云-服务违规封禁提醒解决

腾讯云-服务违规封禁提醒解决 背景解决方案Step1: 查看目标主机上有哪些TCP链接在使用22端口以及该进程的详细信息Step2&#xff1a;删除异常进程&#xff0c;及其可执行文件Step3&#xff1a;处理已经挂起的链接Step4&#xff1a;查看是否存在相关的定时任务Step5&#xff1a;…
阅读更多...
vue - 大文件分片上传之simple-uploader.js的使用

vue - 大文件分片上传之simple-uploader.js的使用

vue - 大文件分片上传之simple-uploader.js的使用 分片上传的思路前端文件切片常见的写法后端常见的写法 关于大文件上传 关于单个文件上传&#xff1a;其实就是前端中的文件通过http传到后端&#xff0c;后端再写入服务器的过程 那单个大文件分片上传&#xff1a;其实就是前…
阅读更多...
SpringBoot中操作Redis解析JsonArray数据为对象List(ruoyi字典值sys_dict为例)

SpringBoot中操作Redis解析JsonArray数据为对象List(ruoyi字典值sys_dict为例)

场景 若依前后端分离版手把手教你本地搭建环境并运行项目&#xff1a; 若依前后端分离版手把手教你本地搭建环境并运行项目_前后端分离的项目怎么跑起来_霸道流氓气质的博客-CSDN博客 在上面搭建系统的基础上&#xff0c;会将系统的字典值缓存进redis中。 看数据格式存储的是…
阅读更多...
大数据数据湖技术Hudi0.12.0版本源码编译

大数据数据湖技术Hudi0.12.0版本源码编译

0 介绍 Apache Hudi&#xff08;Hadoop Upserts Delete and Incremental&#xff09;是下一代流数据湖平台。Apache Hudi将核心仓库和数据库功能直接引入数据湖。Hudi提供了表、事务、高效的upserts/delete、高级索引、流摄取服务、数据集群/压缩优化和并发&#xff0c;同时保…
阅读更多...
WorkPlus AI助理 | 将企业业务场景与ChatGPT结合

WorkPlus AI助理 | 将企业业务场景与ChatGPT结合

近年来&#xff0c;人工智能成为了企业数字化转型的热门话题&#xff0c;作为被训练的语言模型&#xff0c;ChatGPT具备模拟对话、回答问题、写代码、写小说、进行线上内容创作的能力&#xff0c;还能根据聊天的上下文进行互动。作为一款新兴的人工智能应用程序&#xff0c;对于…
阅读更多...
jdk14至16——record关键字

jdk14至16——record关键字

record类型是从14开始预览到16成为正式版的&#xff0c;record类型是一种受限制的类&#xff0c;一般用来封装不可变对象&#xff0c;record类型会自动生成一个全部属性的构造方法&#xff0c;以及属性的get方法&#xff0c;但没有set方法&#xff0c;会自动生成hashCode()、eq…
阅读更多...
JS中深拷贝浅拷贝的区别

JS中深拷贝浅拷贝的区别

深浅拷贝在MDN官方中的表述是这样的&#xff1a; 对象的深拷贝是指其属性与其拷贝的源对象的属性不共享相同的引用&#xff08;指向相同的底层值&#xff09;的副本。因此&#xff0c;当你更改源或副本时&#xff0c;可以确保不会导致其他对象也发生更改&#xff1b;也就是说&a…
阅读更多...
vue下拉框vue字典映射转换失败 字符转数字parseInt :value vue下拉框无法选择 选什么都是最后一个 el-select默认选中 el-select设为只读 input输入框设为只读

vue下拉框vue字典映射转换失败 字符转数字parseInt :value vue下拉框无法选择 选什么都是最后一个 el-select默认选中 el-select设为只读 input输入框设为只读

现象&#xff1a; 解决后&#xff1a; 关键点&#xff1a; 1、value"0" 与 :value"0" 不同&#xff0c;加冒号:试试 2、:value"parseInt(dict.dictValue)" 字符串转int试试 parseInt() 写死下拉框 <el-form-item label"类型" pro…
阅读更多...
COBOL 程序结构

COBOL 程序结构

COBOL 程序结构 COBOL程序结构由部&#xff08;division&#xff09;组成&#xff0c;如下图所示&#xff1a; 这些部简介如下&#xff1a; **Sections&#xff08;节&#xff09;**是程序逻辑的逻辑细分。节是段落的集合。**Paragraphs&#xff08;段&#xff09;**是一个节…
阅读更多...
路面积水监测-路面积水监测系统

路面积水监测-路面积水监测系统

在城市化进程不断加快的背景下&#xff0c;城市道路面临着日益严重的积水问题。持续的降雨和不良的排水系统导致路面积水&#xff0c;给交通运输和城市生活带来了诸多不便和安全隐患。路面积水监测系统旨在易涝点布设内涝积水监测仪&#xff0c;实时了解路面积水情况&#xff0…
阅读更多...
矿井水除氟，污水除氟的工艺分析

矿井水除氟，污水除氟的工艺分析

高矿化度的废水是指含有高浓度溶解性矿物质的废水&#xff0c;通常指的是含有高浓度钠、钙、镁、铁、铝、钾等离子的废水。这些离子通常来自于废水所处的环境、工业或生产过程中使用的原材料和化学品。高矿化度的废水通常具有高盐度、高电导率、高硬度等特征&#xff0c;对环境…
阅读更多...
【Nginx】缓存集成

【Nginx】缓存集成

文章目录 缓存的概念Nginx的web缓存服务Nginx缓存设置的相关指令Nginx缓存设置案例Nginx缓存的清除方式一:删除对应的缓存目录方式二:使用第三方扩展模块 Nginx设置资源不缓存 缓存的概念 缓存就是数据交换的缓冲区(称作:Cache),当用户要获取数据的时候&#xff0c;会先从缓存…
阅读更多...
DOUBLETROUBLE 1

DOUBLETROUBLE 1

文章目录 DOUBLETROUBLE: 1实战演练一、前期准备1、相关信息 二、信息收集1、nmap探测目标靶机端口2、扫描目标网址目录3、访问网站&#xff0c;发现secret下有个图片4、将图片下载5、查看图片所含内容6、破解密码并查看7、登陆邮箱8、创建反弹shell9、上传反弹shell10、监听11…
阅读更多...
【云计算架构】通过新的优化视角查看云架构

【云计算架构】通过新的优化视角查看云架构

仅仅让云部署工作不再是目标。关注构建和部署最佳解决方案的新指标和方法。 随着云计算架构的成熟&#xff0c;我们定义成功的方式也应该成熟。在2021&#xff0c;我指出&#xff0c;优化云计算更多的是二进制过程&#xff0c;而不是模拟过程。 我当时所说的仍然是正确的&#…
阅读更多...
【医学图像】图像分割系列.1

【医学图像】图像分割系列.1

医学图像分割是一个比较有应用意义的方向&#xff0c;本文简单介绍三篇关于医学图像分割的论文&#xff1a; UNeXt&#xff08;MICCAI2022&#xff09;&#xff0c;PHTrans&#xff08;MICCAI2022&#xff09;&#xff0c;DA-Net&#xff08;MICCAI2022&#xff09;。 目录 …
阅读更多...
目标追踪---deepsort原理讲解

目标追踪---deepsort原理讲解

目录 一、多目标追踪的主要步骤 二、sort流程 三、Deepsort算法流程 一、多目标追踪的主要步骤 获取原始视频帧利用目标检测器对视频帧中的目标进行检测将检测到的目标的框中的特征提取出来&#xff0c;该特征包括表观特征&#xff08;方便特征对比避免ID switch&#xff0…
阅读更多...
SQL语句练习附带答案

SQL语句练习附带答案

首先创建数据库filmclub DROP DATABASE IF EXISTS filmclub;CREATE DATABASE filmclub;USE filmclub;CREATE TABLE category (cid INT PRIMARY KEY AUTO_INCREMENT,cname VARCHAR(20) )CHARSETutf8; CREATE TABLE film (fid INT PRIMARY KEY AUTO_INCREMENT,fname VARCHAR(20)…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023