二叉树的概念
满二叉树:二叉树的每一层的节点数都达到最大值
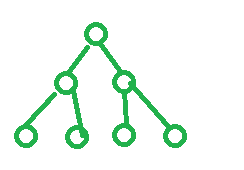
完全二叉树:满二叉树或是从左往右依次变满的树
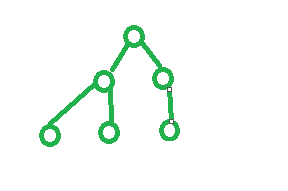
二叉树的数组表示
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

堆结构(优先级队列结构)
完全二叉树
大根堆:每一个子树的头节点的值为子树的最大值
小根堆:每一个子树的头节点的值为子树的最小值
heapinsert过程
数组
| 5 | 3 | 6 | 7 | 7 |
从左往右
指针i = 0 i = 1 i = 2 i = 3 heapinsert过程结束
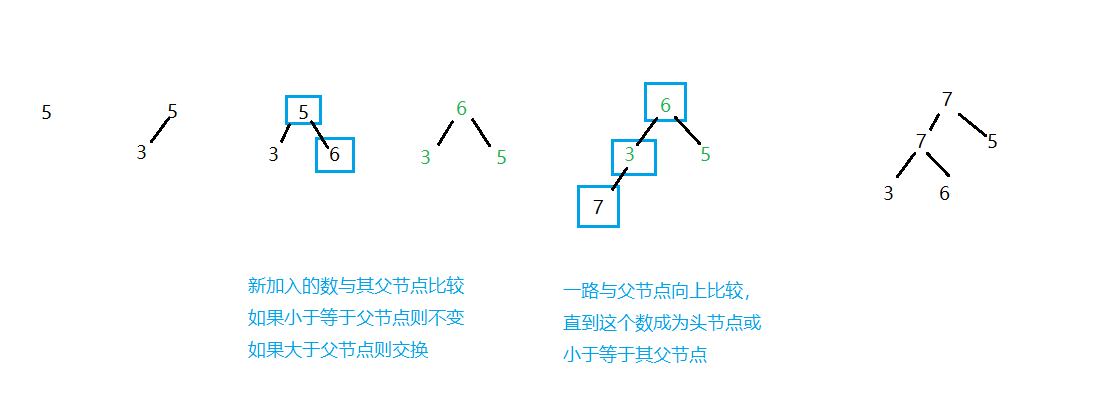
heapinsert过程代码
//用户添加了一个数,放在了index位置,持续向上调整使得整体的二叉树变成大根堆/小根堆
public static void heapInsert(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {//当子节点的值大于父节点的值时,进行交换,并且持续向上比较
//停止的条件一: 子节点的值不再大于父节点的值
//停止的条件二: index = 0,有(0-1)/2 = 0,上式依然不满足
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}heapify 堆化过程
heapinsert过程可以实现取出当前heapsize大小的数组中的最大值——arr[0]
取出最大值后我们把当前数组中的最后一位数移到最前,同时heapsize-1,此时的这个结构仍然是一个二叉树结构、但并不一定是堆结构
我们将头节点的数与其子节点的数比较,如果小于某个子节点,则与其交换;不断重复此操作使最后得到的二叉树为大根堆
| 6 | 3 | 5 | 2 | 3 | 4 |
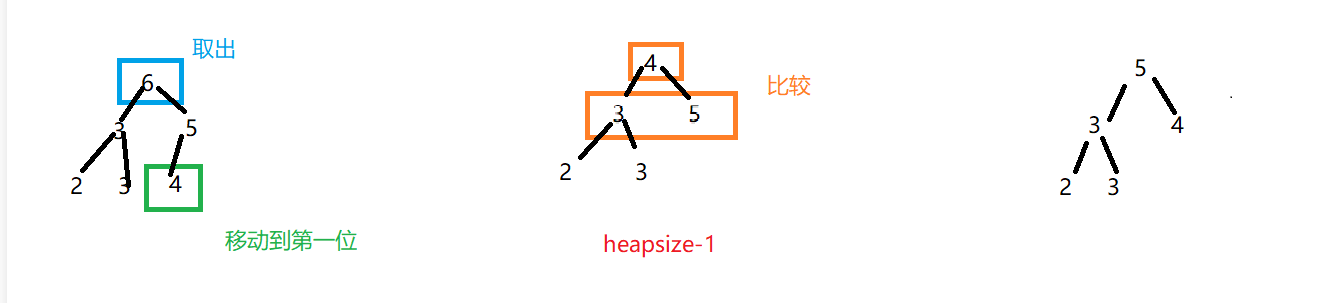
heapify过程代码
public static void heapify(int[] arr, int index, int heapsize) {
//index 当前数组下标; heapSize heapInsert过程中数组的大小,判断左右节点是否越界
int left = index * 2 + 1;//左子节点的下标
int largest = 0;
while (left < heapsize) {//下方还有节点的时候
// 左子节点不越界,那当前一定有子节点;左子节点越界,那右子节点一定越界
//两个子节点中,谁的值大,就把下标给largest
if (left + 1 < heapsize && arr[left + 1] > arr[left]) {//存在右子节点&&右子节点的数较大
largest = left + 1;//右子节点
} else {
largest = left;
}
//父节点与较大子节点中,谁的值大,就把下标给largest
if (arr[index] > arr[largest]) {
largest = index;
}
if (largest == index) {//当前父节点是三个节点中的最大
break;
}
//当前节点作为父节点,与其两子节点进行比较,选出其中最大的与当前位置进行交换
swap(arr, largest, index);
index = largest;//index时向下走的,index获得的值是原来较大子节点的索引
//将当前节点作为下一层的父节点,再次向下选取最大值
left = index * 2 + 1;
}
}当用户修改了在有效区域内的一个值,
如果修改的值大于未修改的值,当前的数往上进行一个heapInsert过程
如果修改的值小于未修改的值,当前的数往下进行一个heapify过程
最终使得修改后仍然是一个堆结构
用户增加/删除一个数,调整结构的复杂度是O(logN)
堆排序
- 进行一个heapInsert过程,将无序的数组变为大根堆的堆结构,在此过程中,记录堆结构大小的heapsize逐渐增加直到heapsize == arr.length
- 取出索引为0的值(堆结构中的最大值),将它与数组中的最后一个位置交换,heapsize-1,堆结构的有效位置减一
- 对index = 0的位置进行一个heapify过程,使得堆结构仍然为一个大根堆结构
- 取出索引为0的值,将它与数组中的最后一个位置交换,heapsize-1
- 对index = 0的位置进行一个heapify
- ........
- 直到最终heapsize的值为0


优化
原方式:通过heapInsert逐个将数添加到堆结构中
优化:实现二叉树的层序遍历(A → B → C → D),最后一层的数向下进行heapify,逐层向上,对头节点heapify后,
最终实现将整个数组转化为堆结构

优化后的复杂度计算:
得出时间复杂度为O(N)
最终代码
package algorithm;
import org.junit.Test;
public class Heap {
@Test
public void test() {
int[] arr = new int[]{3, 5, 6, 4, 7};
heapSort(arr);
for (int i : arr) {
System.out.println(i);
}
}
public static void heapSort(int[] arr) {
if (arr == null || arr.length == 0) {
return;
}
// for (int i = 0; i < arr.length; i++) {//O(N)
// heapInsert(arr, i);//O(logN)
// //通过heapInsert逐个添加数到堆结构中
// }
//优化
for (int i = arr.length; i >= 0; i--) {
heapify(arr, i, arr.length);
}
int heapsize = arr.length;//全部添加完成后堆结构的大小 = 数组的大小
swap(arr, 0, --heapsize);//将索引为0的数与堆结构最后位置的数进行交换,heapsize-1,将最后一位置去除堆结构
while (heapsize > 0) {//O(N)
heapify(arr, 0, heapsize);//O(logN)
//交换上来的数向下进行heapify过程
swap(arr, 0, --heapsize);//O(1)
}
}
//用户添加了一个数,放在了index位置,持续向上调整使得整体的二叉树变成大根堆/小根堆
public static void heapInsert(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {//当子节点的值大于父节点的值时,进行交换,并且持续向上比较
//停止的条件一: 子节点的值不再大于父节点的值
//停止的条件二: index = 0,有(0-1)/2 = 0,上式依然不满足
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
public static void heapify(int[] arr, int index, int heapsize) {
//index 当前数组下标; heapSize heapInsert过程中数组的大小,判断左右节点是否越界
int left = index * 2 + 1;//左子节点的下标
int largest = 0;
while (left < heapsize) {//下方还有节点的时候
// 左子节点不越界,那当前一定有子节点;左子节点越界,那右子节点一定越界
//两个子节点中,谁的值大,就把下标给largest
if (left + 1 < heapsize && arr[left + 1] > arr[left]) {//存在右子节点&&右子节点的数较大
largest = left + 1;//右子节点
} else {
largest = left;
}
//父节点与较大子节点中,谁的值大,就把下标给largest
if (arr[index] > arr[largest]) {
largest = index;
}
if (largest == index) {//当前父节点是三个节点中的最大
break;
}
//当前节点作为父节点,与其两子节点进行比较,选出其中最大的与当前位置进行交换
swap(arr, largest, index);
index = largest;//index时向下走的,index获得的值是原来较大子节点的索引
//将当前节点作为下一层的父节点,再次向下选取最大值
left = index * 2 + 1;
}
}
public static void swap(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}
拓展

假设k = 6,那么我们先将前七个数排成一个小根堆,保证在索引为0的位置上是前七个数的最小值。由于数组本身几乎有序,其现在所在的位置距离它排完序后的位置不会超过k,那么索引为0位置上的数一定是整个数组上的最小值
我们将索引为0的数移出小根堆,将下一个数(也就是索引为7的数字,第8个数字)加入小根堆,在索引1到7的小根堆中的最小值即为索引为1上的值
如此向后推进,index = arr.length 后,仍然移出最前的数直到堆结构为空
复杂度O(N*logk)
package algorithm;
import org.junit.Test;
import java.util.PriorityQueue;
public class SortArrayDistanceLessK {
@Test
public void test(){
int[] arr = new int[]{8,4,4,9,10};
sortArrayDistanceLessK(arr,3);
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
public static void sortArrayDistanceLessK(int[] arr, int k) {
PriorityQueue<Integer> heap = new PriorityQueue<>();//优先级队列,默认小根堆
int index = 0;
for (index = 0; index < Math.min(arr.length, k); index++) {//一般认为k < arr.length 防止取k的值过大导致错误
heap.add(arr[index]);//将前k+1个数添加到堆结构中
}
int i = 0;
for (i = 0; index < arr.length; i++, index++) {
heap.add(arr[index]);//添加后一个数,当index = arr.length时,跳出for循环结构
arr[i] = heap.poll();//移出最小值
}
while(!heap.isEmpty()){//index不再增加,i自增,堆结构不断减小
arr[i++] = heap.poll();
}
}
}