概述

向量

理解

1. 直观理解

   • 行向量：把数字排成一行A = $[45]$
   • 列向量：把数字排成一列A = $\left[\begin{array}{c}4\\ 5\end{array}\right]$

2. 几何意义

   默认在基底条件下(直角坐标系)中的坐标表示的一个点，也可以理解以原点为起点，到目标终点A的有向线段

   

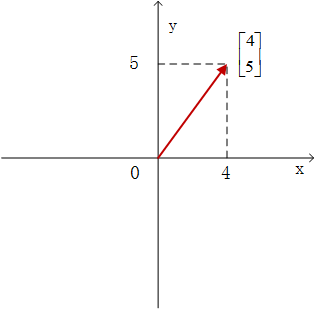
   因此，向量中成分个数就是向量的维度。

3. 注意

   • 充当数据的载体，向量的每个维度都作为事物的一种属性，比如一次考试的成绩，语文98分、数学89分，英语100分。这时用向量表示为$\left[\begin{array}{c}98\\ 89\\ 100\end{array}\right]$
   • 一般使用列向量（默认）：1、节省空间，2、在进行变换时类似于函数利于理解$Ax$与$f(x)$

4. Python演示

   1. 生成行向量

      import numpy as np
      
      A = np.array([1, 2, 3, 4])
      print(A)
      

      [1 2 3 4]
      

   2. 生成列向量（便于计算表示成$n\ast 1$的矩阵)

      import numpy as np
      
      A = np.array([[1, 2, 3]])
      print(A)
      print(A.T)
      

      [[1 2 3]]
      [[1]
       [2]
       [3]]
      

向量运算

1. 向量加法

   两个维度相同的向量才能进行加法，对应维度元素相加即可。

   

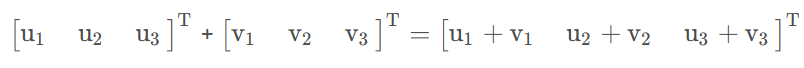
   从空间的角度理解。

   就是两个向量的合向量。

   

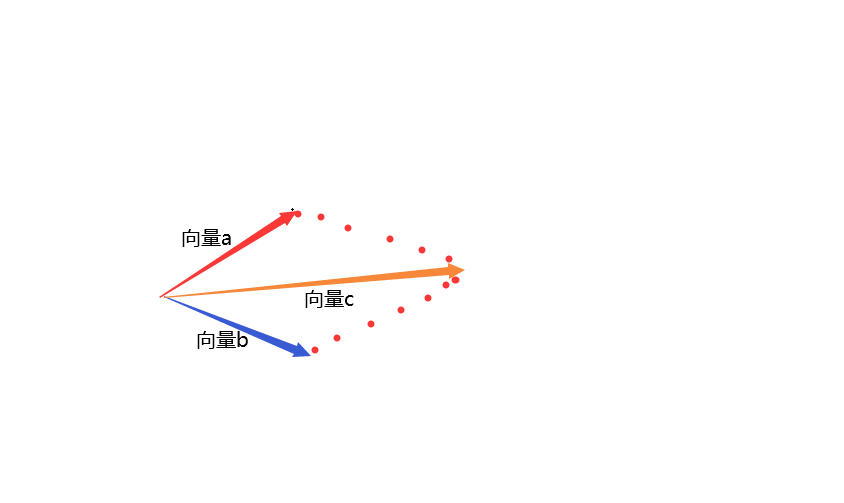
   import numpy as np
   
   # 定义两个向量
   a = np.array([1, 2, 3])
   b = np.array([4, 5, 6])
   
   # 向量加法
   c = a + b
   print(c)
   

   [5 7 9]
   
   

2. 向量数乘

   把数c与向量每个元素分别相乘，结果向量保持维数不变，直观理解，就是将向量沿着原来方向拉伸相应倍数，最终发现与运算数的符号有关。

   

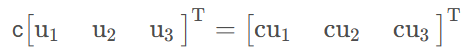
   import numpy as np
   
   # 定义一个向量
   a = np.array([1, 2, 3])
   
   # 向量数乘
   k = 2
   b = k  * a
   
   print(b)
   

   [2 4 6]
   

3. 线性性质阐述

   通过以上两个向量性质阐述，我们总结一下线性代数这么课中线性的内涵，凡是满足以上加法和数乘性质的代数运算，我们就成为线性运算，如果一个代数系统，满足线性运算，那么我们称这个代数系统为线性代数。线性代数就是研究其中性质的一门课。

4. 向量的内积

   向量$u$和向量$v$內积定义如下：

   $u\cdot v=[u_1{u}_2{u}_3][v_1{v}_2{v}_3{]}^T=u_1{v}_1+u_2{v}_2+u_3{v}_3$

   其物理意义是：$u\cdot v=|u||v|cos\theta$，也就是向量u在v上的投影长度与v模的乘积，可以方便求出u其在v上的投影

   

5. 向量的外积

   我们只讨论二维平面和三维空间中的向量外积：

   • 在二维平面中：

     $u\times v=[u_1{u}_2{]}^T\times [v_1{v}_2{]}^T=u_1{v}_2-u_2{v}_1$

     $|u\times v|=|u||v|sin\theta$,表示两个向量张成的平行四边形面积

     

   • 在三维平面中：

     $u\times v=[u_1{u}_2{u}_3{]}^T\times [v_1{v}_2{v}_3{]}^T=[u_2{v}_3-u_3{v}_2{u}_3{v}_1-u_1{v}_3{u}_1{v}_2-u_2{v}_1]$

     表示两个向量所表示平面的法向量。

6. 向量的线性组合

   在向量加法和数乘的基础上的组合应用。

基底与向量的坐标表示

基底与向量的深入

对于向量$u=[45{]}^T$而言，我们一直以来都很理所应当的认为：他表示一条在$x$轴上投影为4，$y$轴上投影为 5的有向线段，其坐标为$(4,5)$。这其实是基于了一个我们没有刻意强调的前提：我们是利用了方向为$x$轴、$y$轴正方向且长度为1的两个向量$e_x=[10{]}^T$,$e_y=[01{]}^T$作为讨论基准。因此向量u的完整写法是:$u=4e_x+5e_y,u=4[10{]}^T+5[01{]}^T$。

这里作为基准的向量$e_x,e_y$便是基底，具体作用是当做参考系。基底的每个成员称作基向量。而坐标，就是各基向量前的系数。在已有基底的基础上，空间中的向量表示为坐标的形式，也可以看成基向量的线性组合。而且在不做说明的情况下，一般基向量选取坐标中正方向且长度为1的向量。

综上：向量$u$的准确说法为：在基底$(e_x,e_y)$下，以原点为出发点，终点为坐标$(4,5)$的有向线段。

基底与向量选取与表示

同一向量在不同的基底下表示为不同坐标

在向量空间中的同一个向量$u$，当我们基底分别选取$[10{]}^T$、$[01{]}^T$和$[\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}{]}^T$、$[-\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}{]}^T$时,在假设前者条件下表示为$u=[45{]}^T$，则在后者为基底的情况下表示为$[\frac{9}{\sqrt{2}}\frac{1}{\sqrt{2}}{]}^T$。

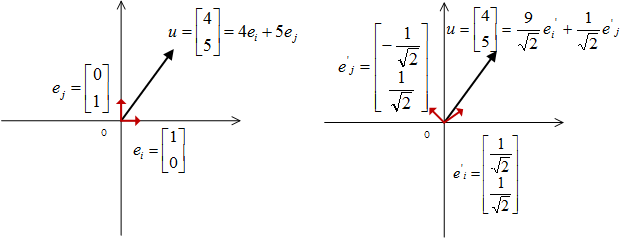
基底的特殊性

1. 基向量满足线性无关

   在每个向量空间(解释在下)中每个向量都是唯一的，表示也是唯一的。当存在基向量线性相关时，对于空间中的向量表示就不是唯一了。

2. 基底的数量要足够

   对于$n$维空间，必须要有$n$个线性无关的向量作为基底。拿三维空间举例，如果线性无关的基向量只有两个，那么其再怎么组合成的向量也只能在一个平面内，平面外的向量无法表示。

3. ${\mathbb{R}}^n$空间($n$维向量空间)与$n$维空间的区别

   ${\mathbb{R}}^n$空间表示所有$n$维向量的集合(默认直角坐标系的基底)，其中每个向量是$n$维。

   $n$ 维空间是指由 $n$ 个线性无关的向量所张成的向量空间。

   区别是$n$维空间的基向量不一定是$n$维向量，可以是更高的维度，但空间中所有向量都可以在${\mathbb{R}}^n$得以表示。

   ${\mathbb{R}}^n$空间等价于$n$ 维空间（也就是其中的所有向量都可以表示为$n$维度)，只是可能所选取的基底不同，高维的向量空间一定能包含低维向量空间，我们称低维空间为高维的向量空间。

张成空间

一组向量，所有线性组合的向量构成的集合我们称之为这组向量张成的空间。

• $n$个线性无关的向量张成的是${\mathbb{R}}^n$空间
• $n$个向量中，$m$个线性无关的向量，张成的是${\mathbb{R}}^m$空间。

张成的向量空间维度与向量具体维度无关，原因即${\mathbb{R}}^n$空间($n$维向量空间)与$n$维空间的区别。

• $n$个线性无关的向量张成的是${\mathbb{R}}^n$空间
• $n$个向量中，$m$个线性无关的向量，张成的是${\mathbb{R}}^m$空间。

张成的向量空间维度与向量具体维度无关，原因即${\mathbb{R}}^n$空间($n$维向量空间)与$n$维空间的区别。