看这篇文章前需要看下前面三篇文章,最起码第一第二篇是需要看一下的
斐波那契数列数列相关简化1_鱼跃鹰飞的博客-CSDN博客
斐波那契数列数列相关简化2_鱼跃鹰飞的博客-CSDN博客
算法玩的就是套路,练练就熟悉了
再来一个:
用1*2的瓷砖,把N*2的区域填满
返回铺瓷砖的方法数
这题一看也有些懵逼,我先画个图:
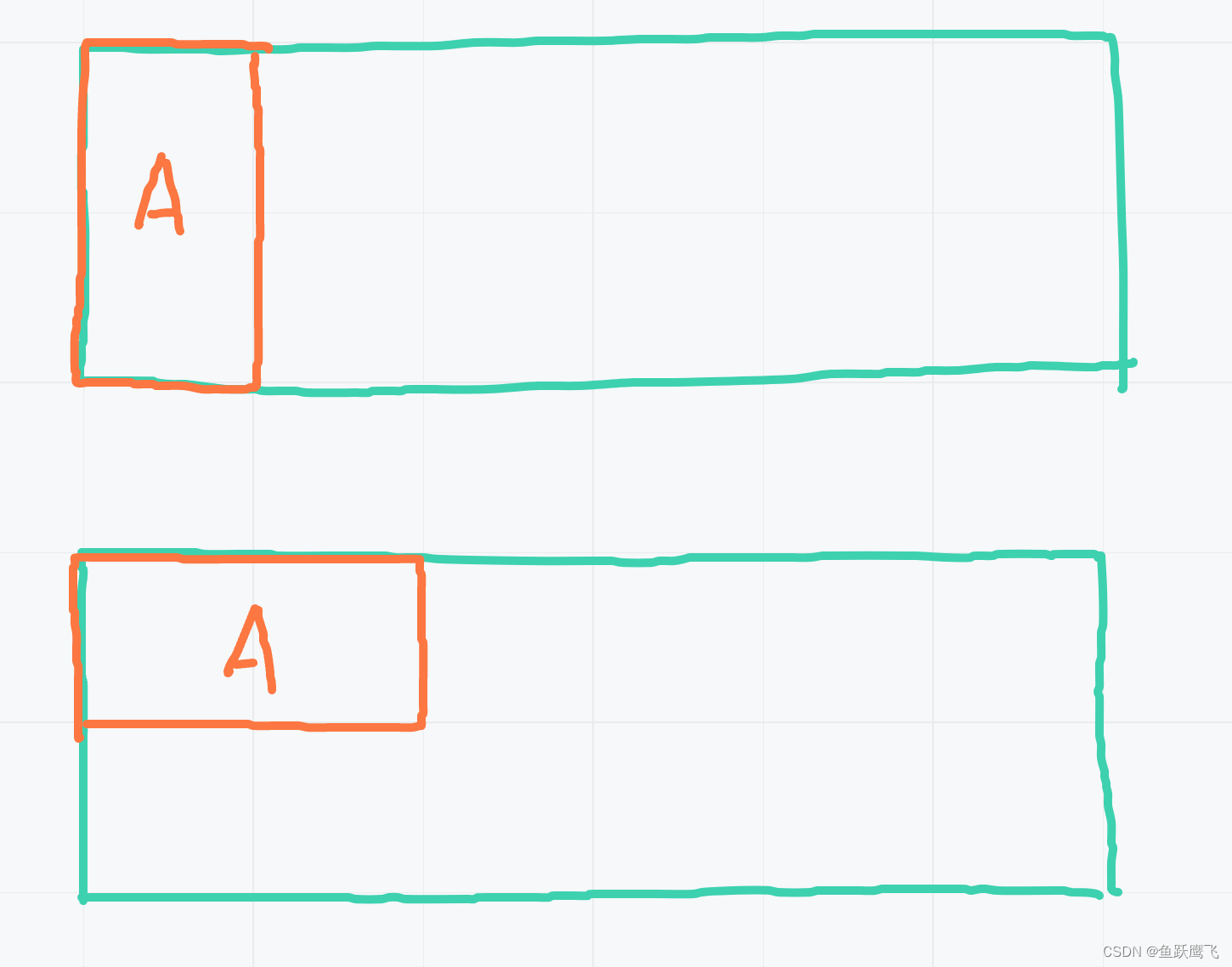
哈哈,图简单吧,但是我想说什么你应该是懂的
如果第一块砖竖着铺,那后面n-1的区域使用黑盒方法选择同样的方法算数量就好了
如果第一块横着铺,那第二块只能横着铺,后面的区域就剩下n-2了,同样使用黑盒方法计算数量就好了
下面是递归的方法:
/**
* 黑盒递归方法,返回剩余n*2块的区域能铺满的方法数
* @param n
* @return
*/
public static int ways(int n) {
if(n < 1) return 0;
if(n == 1 || n == 2) return n;
//第一种:n里面的第一块横着铺,第二块也没得选,只能横着铺
int p1 = ways(n - 2);
//第二种:n里面的第一块竖着铺,第二块开始的n-1块可以随意选择
int p2 = ways(n -1);
//第一块横着和第一块竖着肯定是不同的方法,加一起
return p1 + p2;
}分析这个过程不难发现,这也是没有条件的严格位置依赖,符合我们第二篇文章中说的优化条件
依然是二阶矩阵,别的不多说了,上代码吧:
package dataStructure.fibonacci;
import static dataStructure.fibonacci.FibonacciStandard.matrixPower;
import static dataStructure.fibonacci.FibonacciStandard.product;
/**
* 用1*2的瓷砖,把N*2的区域填满
*
* 返回铺瓷砖的方法数
*/
public class UseTileFullfill {
/**
* 黑盒递归方法,返回剩余n*2块的区域能铺满的方法数
* @param n
* @return
*/
public static int ways(int n) {
if(n < 1) return 0;
if(n == 1 || n == 2) return n;
//第一种:n里面的第一块横着铺,第二块也没得选,只能横着铺
int p1 = ways(n - 2);
//第二种:n里面的第一块竖着铺,第二块开始的n-1块可以随意选择
int p2 = ways(n -1);
//第一块横着和第一块竖着肯定是不同的方法,加一起
return p1 + p2;
}
/**
* 根据类似斐波那契数列的严格推理方式进行变化-使用矩阵的某次方
* 时间复杂度O(logN)
* @param n
* @return
*/
public static int ways2(int n) {
if(n < 1) return 0;
if(n == 1 || n == 2) return n;
/*//第一种:n里面的第一块横着铺,第二块也没得选,只能横着铺
int p1 = ways(n - 2);
//第二种:n里面的第一块竖着铺,第二块开始的n-1块可以随意选择
int p2 = ways(n -1);
//第一块横着和第一块竖着肯定是不同的方法,加一起
return p1 + p2;*/
//根据递归方法算得前1,2,3,4项的结果分别是1,2,3,5
//|f(3) f(2)| = |f(2) f(1)| * base
//假设base是{{a, b}{c, d}}
//|3 2| = |2 1| * base->2a + c = 3 2b + d =2
//|5 3| = |3 2| * base->3a + 2c = 5 3b + 2d = 3
//通过上面两个方程可以得到a=1, c = 1, b = 1 d = 0
int[][] base = {{1,1},{1,0}};
int[][] matrix21 = {{2,1}};
int[][] matrix = matrixPower(base, n - 2);
matrix = product(matrix21, matrix);
return matrix[0][0];
}
public static void main(String[] args) {
int n = 6;
int ways1 = ways(n);
System.out.println(ways1);
int ways2 = ways2(n);
System.out.println(ways2);
}
}
详细注释,方法都是用的以前的类里的,懒得写了,都是一样的,看不懂的私信我。
这个系列的题目先练到这里吧,相信对你已经没有任何挑战了,还想练的话很多递归的题目都能练这个,我再提供一个题目吧:
一个人可以一次往上迈1个台阶,也可以迈2个台阶
返回这个人迈上N级台阶的方法数