多层感知机学习XOR实例
- 多层感知机介绍
- 使用多层感知机学习XOR实例
- 传统统计数学方法(传统机器学习)
- 使用多层感知机学习XOR
- 总结
多层感知机介绍
多层感知机(Multilayer Perceptron,MLP),又称为深度前馈网络(Deep Feedforward Network)。多层感知机是用来近似某个函数
f
∗
f^*
f∗。即对于分类器,函数
y
=
f
∗
(
x
)
y=f^*(x)
y=f∗(x),多层感知机定义映射关系为
y
=
f
(
x
;
θ
)
y=f(x;\theta)
y=f(x;θ),并学习参数
θ
\theta
θ的值。这种网络结构被称为前向是因为信息流过
x
x
x的函数,流经用于定义
f
f
f的中间计算过程,最终到达输出
y
y
y。该模型的输出和模型本身之间是没有反馈连接。当前馈神经网络被扩展包含反馈连接时,它们被称为循环神经网络(RNN)。
前馈神经网络之所以被称为网络,是因为它们通常用许多不同函数复合在一起来表示。该模型与一个有向无环图相关联,而图描述了函数是如何复合在一起的。例如,有三个函数
f
(
1
)
f^{(1)}
f(1)、
f
(
2
)
f^{(2)}
f(2)和
f
(
3
)
f^{(3)}
f(3)连接在一个链上以形成
f
(
x
)
=
f
(
3
)
(
f
(
2
)
(
f
(
1
)
)
)
f(x)=f^{(3)}(f^{(2)}(f^{(1)}))
f(x)=f(3)(f(2)(f(1)))。在这种情况下,
f
(
1
)
f^{(1)}
f(1)被称为网络的第一层,
f
(
2
)
f^{(2)}
f(2)被称为第二层,以此类推,链的全长称为模型的深度。前馈神经网络的最后一层被称为输出层。而学习算法使用的中间层用以更好的拟合函数的层级被称为隐藏层。这里多层感知机引入了隐藏层,因此我们还要在设计网络的时候,考虑选择这些隐藏层的激活函数。
使用多层感知机学习XOR实例
XOR函数即是异或逻辑函数。这是一个关于两个二进制值
x
1
x_1
x1和
x
2
x_2
x2的运算。当两个输入值有且只有一个值为1时,函数输出为1,其余结果均为0。
因此,该学习任务就是拟合XOR函数,即是满足函数在点
X
=
{
[
0
,
0
]
⊤
,
[
0
,
1
]
⊤
,
[
1
,
0
]
⊤
,
[
1
,
1
]
⊤
}
\mathbb{X}=\{[0,0]^\top,[0,1]^\top,[1,0]^\top,[1,1]^\top\}
X={[0,0]⊤,[0,1]⊤,[1,0]⊤,[1,1]⊤}上的取值。
我们可以先尝试使用传统的统计数学方法。
传统统计数学方法(传统机器学习)
使用传统统计数学方法,我们将该问题视为函数回归问题。以均方误差MSE作为损失函数,如下:
J
(
θ
)
=
1
4
∑
x
∈
X
(
f
∗
(
x
)
−
f
(
x
;
θ
)
)
2
J(\theta)=\frac{1}{4}\sum_{x\in\mathbb{X}}(f^*(x)-f(x;\theta))^2
J(θ)=41x∈X∑(f∗(x)−f(x;θ))2
然后再定义目标函数
f
(
x
;
θ
)
f(x;\theta)
f(x;θ),
θ
\theta
θ包含
ω
\omega
ω和
b
b
b,如下:
f
(
x
;
ω
,
b
)
=
x
⊤
ω
+
b
f(x;\omega,b)=x^\top\omega+b
f(x;ω,b)=x⊤ω+b
再使用统计数学的正规方程关于
ω
\omega
ω和
b
b
b最小化
J
(
θ
)
J(\theta)
J(θ),解得
ω
=
0
\omega=0
ω=0而
b
=
1
2
b=\frac{1}{2}
b=21 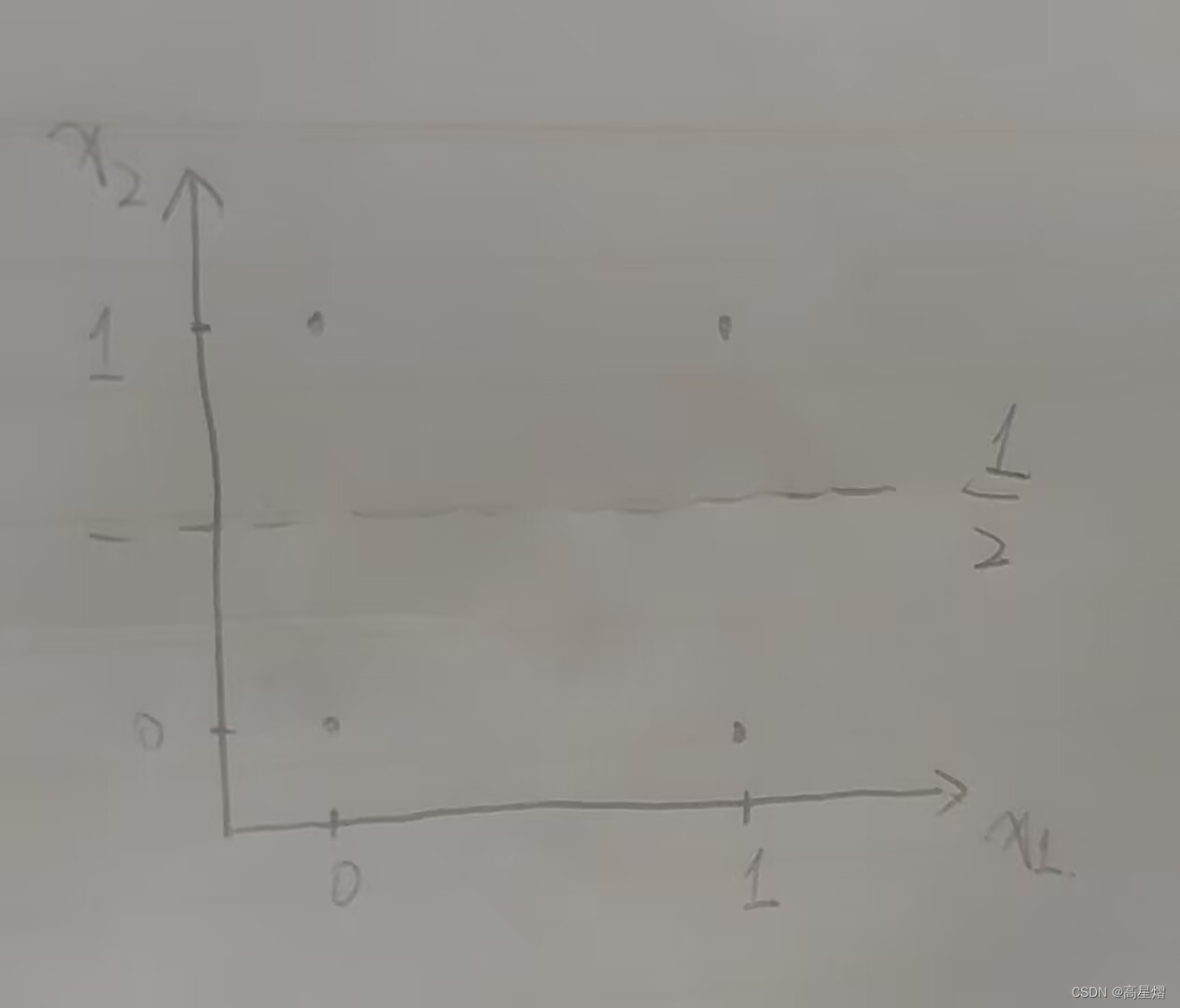
学习得到得到的线性模型是任意点都输出均为1/2。原因是这个非线性的函数均匀分布,使用线性回归就会将函数拟合到中值线上。
显然,这种方案是不符合我们的预期的。XOR函数是非线性的,通过解线性目标函数的正规方程来拟合是不合理的做法,同样,对于二进制输入问题建模使用MSE作为损失函数也是有欠妥当。然而,求解线性问题永远都要比直接求解非线性问题要简单的多。有一种解决该问题的思路是学习一个特征空间,然后在这个空间中,我们可以使用线性的函数进行表示这个非线性的解。这里就是要通过空间的非线性来割裂函数的线性。
这里我们就可以引入多层感知机
使用多层感知机学习XOR
因为XOR是二进制数据输入,且输出状态仅为二进制的两种情况。所以,这里可以采用一个简单的网络结构。
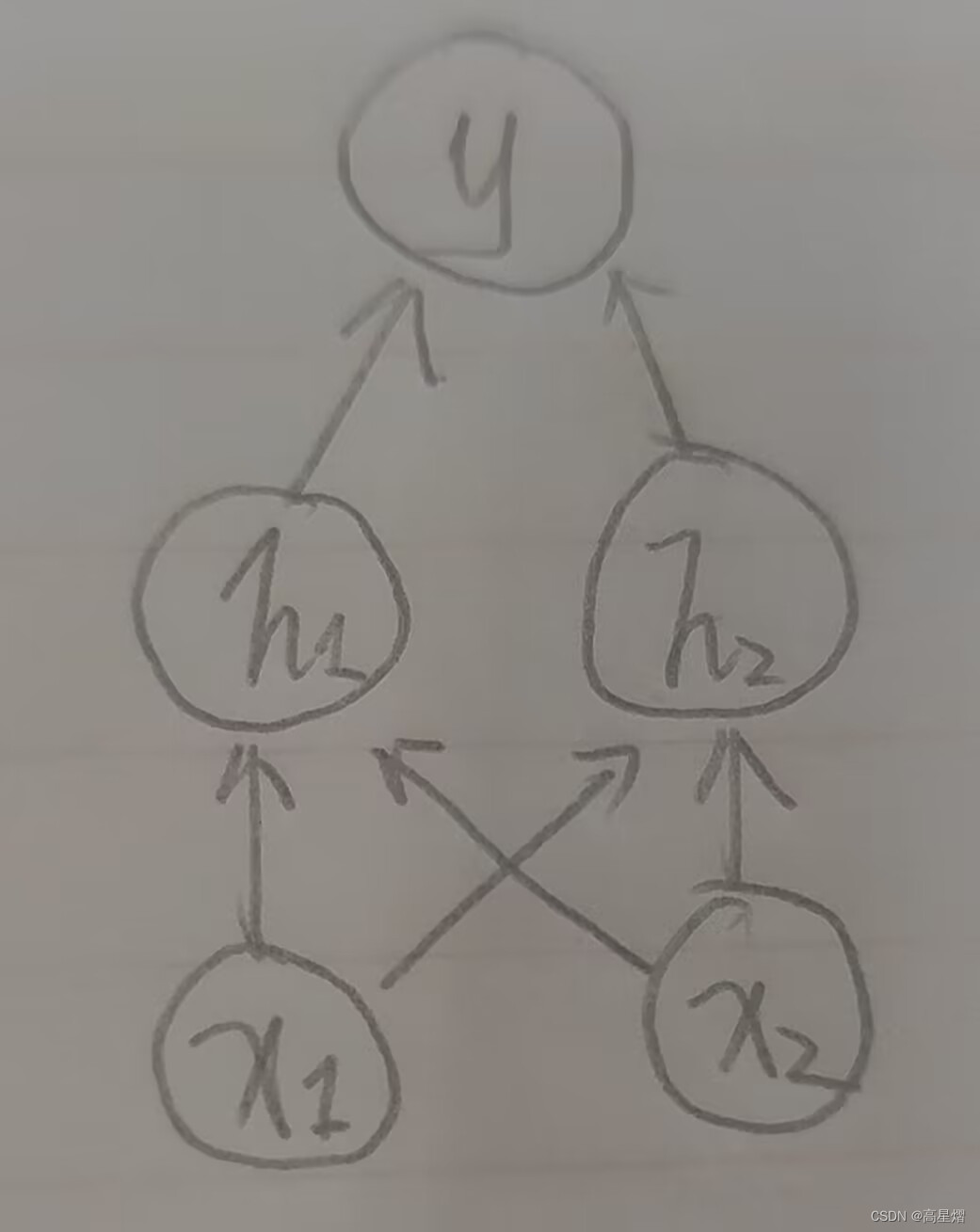
上图中的网络结构由两个函数连接:
h
=
f
(
1
)
(
x
;
W
,
c
)
h=f^{(1)}(x;W,c)
h=f(1)(x;W,c)和
y
=
f
(
2
)
(
h
;
ω
,
b
)
y=f^{(2)}(h;\omega,b)
y=f(2)(h;ω,b)。完整的输入到输出就是
y
=
f
(
x
;
W
,
c
,
ω
,
b
)
=
f
(
2
)
(
f
(
1
)
(
x
)
)
y=f(x;W,c,\omega,b)=f^{(2)}(f^{(1)}(x))
y=f(x;W,c,ω,b)=f(2)(f(1)(x))。
一般地,神经网络通过仿射变换后,使用特定的非线性函数作为激活函数来实现非线性的描述。 因此,这里选用激活函数
g
g
g后,函数
f
(
1
)
f^{(1)}
f(1)为:
h
=
g
(
W
⊤
x
+
c
)
h=g(W^\top x+c)
h=g(W⊤x+c),这里W是线性变换的权重矩阵,c为偏置量。而对于激活函数
g
g
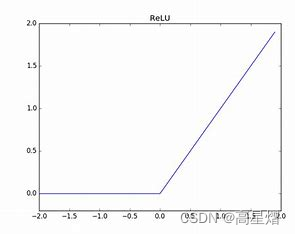
g的选择,这里使用比较普遍的整流线性单元(ReLU)。如下式:
g
(
z
)
=
m
a
x
{
0
,
z
}
g(z) = max \{0,z\}
g(z)=max{0,z}
因此,整个网络的函数式为:
f
(
x
;
W
,
c
,
ω
,
b
)
=
ω
⊤
m
a
x
{
0
,
W
⊤
+
c
}
+
b
f(x;W,c,\omega,b)=\omega^\top max\{0 , W^\top+c\}+b
f(x;W,c,ω,b)=ω⊤max{0,W⊤+c}+b
然后,我们就可以通过梯度优化的方法求得XOR问题的解。
W
=
[
1
1
1
1
]
W = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}
W=[1111]
c
=
[
0
−
1
]
c = \begin{bmatrix} 0 \\ -1 \end{bmatrix}
c=[0−1]
ω
=
[
1
−
2
]
\omega = \begin{bmatrix} 1 \\ -2 \end{bmatrix}
ω=[1−2]
b
=
0
b=0
b=0
然后,我们可以把XOR函数的输入带入进行验证,
X
=
{
[
0
,
0
]
⊤
,
[
0
,
1
]
⊤
,
[
1
,
0
]
⊤
,
[
1
,
1
]
⊤
}
\mathbb{X}=\{[0,0]^\top,[0,1]^\top,[1,0]^\top,[1,1]^\top\}
X={[0,0]⊤,[0,1]⊤,[1,0]⊤,[1,1]⊤},写作矩阵:
X
=
[
0
0
0
1
1
0
1
1
]
X = \begin{bmatrix} 0&0 \\ 0&1\\ 1&0\\ 1&1 \end{bmatrix}
X=
00110101
神经网络第一步将输入矩阵乘以第一层权重矩阵:
X
W
=
[
0
0
1
1
1
1
2
2
]
XW=\begin{bmatrix} 0&0 \\ 1&1\\ 1&1\\ 2&2 \end{bmatrix}
XW=
01120112
加上偏置向量c,得:
[
0
−
1
1
0
1
0
2
1
]
\begin{bmatrix} 0&-1 \\ 1&0\\ 1&0\\ 2&1 \end{bmatrix}
0112−1001
再通过整流线性单元变换:
[
0
0
1
0
1
0
2
1
]
\begin{bmatrix} 0&0 \\ 1&0\\ 1&0\\ 2&1 \end{bmatrix}
01120001
然后,再乘以权重向量
ω
\omega
ω:
ω
=
[
1
−
2
]
\omega=\begin{bmatrix} 1\\ -2 \end{bmatrix}
ω=[1−2]
得到输出:
y
=
[
0
1
1
0
]
y = \begin{bmatrix} 0 \\ 1\\ 1\\ 0 \end{bmatrix}
y=
0110
总结
这里以XOR为例,我们比较两种解决方案,对于非线性的模型处理中,单纯的线性模型的回归是难以应付的,我们通常使用神经网络才能比较好的描述其模型的非线性,而神经网络的非线性就会导致代价函数大多非凸,以至于使得常规的线性回归、线性方程求解或是支持向量机都难以收敛到一个点,并且,理论上凸优化从人一个初始参数出发都最终达成收敛,但是非凸的损失函数的随机梯度下降是不会有这种收敛保证,对于初始的参数值也异常敏感(直接关系到下降的最低点是局部的最低还是全局的最低)。因此我们采用基于梯度的方式进行优化。而对于如何计算神经网络的下降梯度,以及上述的XOR例子中的,多层感知机的参数学习过程,下一篇我将详细进行叙述。