2022年深圳杯数学建模

B题 基于用电可靠性的配电网规划

原题再现：

  如果一批用户变压器（下面简称用户）仅由一个电源变电站（下面简称电源）供电，称为单供。这时配电网由电线和开关联接成以电源为根节点的树状结构图，使得每个用户所在顶点都在图中有路（电线）联接到电源根节点。
  一些电力用户一旦发生停电，无论停电时间长短，都会带来较大损失，降低用电满意度。因此，定义
  用户用电可靠性：指定时间段内不因配电网故障停电或限电的概率。
  为了提升用户用电可靠性，可在两个电源的单供配电网之间建立联络线，并增设开关和扩充电源可供电功率，形成双电源供电配电网（简称双供配电网，如下图所示）。

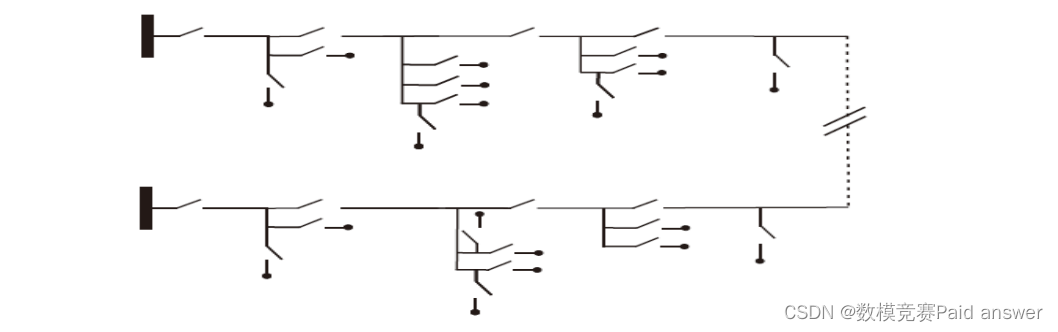
  开关设置原则：
  1. 配电网中开关（电源出线后开关除外）的设置必须使得网中某处发生故障时，通过开关隔离故障后，保持供电的用户需求功率之和最大化；
  2. 在网上任意一点到电源的所有路中，可以通过设置开关状态使得仅有一条是通路；
  3. 配电网中开关的设置包含但不限于以下情况：每个用户前端有开关，每个分岔点后端的每条支路上有开关，双供配电网的每条联络线上有开关。
  配电网设施可靠性单元划分及其可靠性：
  忽略电源至它的后端第一个开关部分，忽略用户至它的第一个前端开关部分，配电网设备可靠性（故障）单元由电源、用户、开关，以及仅含两个开关之间的路（下面称为故障单元路）构成。每个单元设备在指定时间段内正常运行的概率称为单元设备可靠性，它等于 1 减去该单元设备的故障率。
  双供配电网用户供电调度原则：
  (1) 满足一个用户全部需求功率，否则断开该用户；
  (2) 首先满足各自单供配电网内用户的需求；双供电源多余功率的分配优先提高
  全配电网供电功率总和，然后提升全配电网最低的用电可靠性。
  问题：
  1. 已知一个电源和一批用户的平面坐标、每个用户用电功率需求、每个设备单元建造费用（数据格式见附录）。设计建造费用最低的单供配电网供电所有用户，给出树状配电网的分叉点坐标，并计算该配电网中每个用户的用电可靠性。
  2. 已知两个电源和一批用户的平面坐标、每个用户用电功率需求、每个设备单元建造费用（数据格式见附录）。设计建造费用最低的两个单供配电网，使得每个用户都被供电。给出树状配电网的分叉点坐标，并计算该配电网中每个用户的用电可靠性。
  3. 在第 2 题结果的基础上，通过建立两个单供配电网之间的联络线，增设开关，并扩充电源可供电功率，形成双供配电网，以提高用户的用电可靠性。假设两个电源各自能扩充可供电功率 50%，建造双供配电网总花费上限为 X，求使得双供配电网中最低的用电可靠性达到最大的联络线和开关设计。画出联络线拓扑简略图，并计算双供配电网中每个用户的用电可靠性。
  4. 在第 2 题结果的基础上，通过建立两个单供配电网之间的联络线，增设开关，并扩充电源可供电功率形成双供配电网，以提高用户的用电可靠性。假设两个电源各自能扩充可供电功率 50%，设计建造总费用最低的双供配电网，使得双供配电网中每个用户的用电可靠性不低于 Y%。画出联络线拓扑简略图，并计算双供配电网中每个用户的用电可靠性。

整体求解过程概述(摘要)

  合理的配电网规划对电力系统的经济性与安全性有显著影响。为降低配电网建设成本、提高用户用电可靠性，本文提出了基于 TSP 的线路规划模型，给出了配电网联络线的规划方法以及用户用电可靠性的计算式。
  针对问题一，使用 k-means 聚类法将用户分配到不同的单元网络，建立了基于 TSP的单元网络连接模型，最后使用遗传算法求解得到系统的拓扑结构以及用户的用电可靠性。首先选定聚类数 k，以聚类中心作为分叉点，将不同分叉点的连接视为输电线路的建设，以干路线路经过分叉点的顺序作为解向量，由此建立基于 TSP 的线路规划模型，带入遗传算法求解得到对应的费用。通过设置不同的聚类数 k 求解得到对应的费用，通过分析得出最佳的聚类数为 k = 10，并给出了对应的系统拓扑结构与用户用电可靠性。
  针对问题二，首先计算每个用户到两电源的距离，并以“距离较近者优先”为依据将其划分为两个独立的配电系统，然后利用问题一的模型对两个配电系统分别求解得到其线路规划，从而给出总体的系统拓扑结构与用户用电可靠性，并对模型的参数做了分析。
  针对问题三，引入决策变量描述联络线的建设情况，以最低用户用电可靠性尽量大为目标，建立优化模型，利用产生随机解的方法得到较优解。通过假设联络线不交叉简化了模型，引入决策变量 ai, bi，以网络拓扑结构、费用上限和变量间的制约为约束条件，建立最优化模型。由于变量结构复杂，故采用生成大量随机解的方法求得了较优解，最后给出了系统拓扑结构与用户用电可靠性。最后对模型做了分析，指出最佳的费用上限为 X = 1.05 × 105。
  针对问题四，只需在问题三的基础上修改优化目标与部分约束条件即可。将优化目标调整为总费用尽量小，以网络拓扑结构、用户用电可靠性下限和变量间的制约为约束条件建立最优化模型，采用问题三的方法求解，得到系统拓扑结构与用户用电可靠性。最后对模型做了分析，得出最佳的用户用电可靠性下限为 Y % = 0.932。文章的最后总结了模型的优缺点与改进方向。

模型假设：

  1. 假设各种故障的发生是相互独立的；
  2. 不考虑地形因素，即线路的建设成本仅与线路长度有关；
  3. 假设功率的输送方向是单向的；
  4. 假设无重大自然灾害影响；
  5. 假设用户功率需求恒定。

问题分析：

问题一分析

  问题一已知电源、用户坐标及用户的功率需求，需要我们在总费用尽量小的前提下确定干路分叉点及用户的用电可靠性。首先可以采用 k-means 聚类方法将用户按照距离随机地聚为 k 类，即得到 k 个单元网络，以每一个类的平均位置 (Xi, Yi) 作为分叉点的坐标，单元网络内部采用直接相连的方式供电。对于单元网络之间的连接，可以通过构造 0-1 变量的方式，将其转化为旅行商问题，其目标为总费用最小。由于数据量过大，故可以采用智能算法求解得出整个干路的连接方式，进而可以通过概率论的知识求解出每个单元网络的可靠性。

问题二分析

  问题二要求用两个电源规划配电网络，需要在满足每个用户功率需求的条件下使得总费用最小。首先分别求解每个用户 i 到两个电源的距离 s1i, s2i，以距离的远近作为划分依据，将用户分配到两个配电系统中。对于每个独立的两个配电系统，可以直接利用问题一的模型求解，得到每个单元网络的分叉点以及用户用电可靠性。

问题三分析

  问题三在问题二建立的配电系统之间建立联络线，在总费用不超过给定上限 X 的前提下规划联络线，使得用户用电可靠性的最小值尽量大。可以通过引入用于描述联络线建设情况的决策变量 ai, bi，通过限定联络线不交叉简化模型复杂度，并确立价格约束和联络线的拓扑约束，以最低用户可靠性为目标函数建立最优化模型。由于决策变量的构造方式复杂，难以用常规优化算法求解，因此采用蒙特卡洛方法产生大量随机解的方法求得较优解。

问题四分析

  问题四在问题二的基础上建设联络线，在用户用电可靠性下限不低于给定 Y % 的前提下规划联络线，使得总费用尽量小。可以沿用问题三的模型，只需将问题三的优化目标调整为约束条件，将问题三的总费用约束调整为优化目标即可求解。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：(代码和文档not free)

论文及程序仅供学习与参考

%% 定值设定
L = 10;% 地图尺寸，单位： km
%% 初始化用户
N_user = 40;
% for ii=1:N_user
% user(ii).location = rand([1,2])*10;
% user(ii).power = 10*rand;
% user(ii).cluster_idx = [];
% end
k=10;
%%
%sub_net记录了每个类中的点，以及所求的中心点，以及每个类所含的数目
% [user, sub_net] = K_Means(user, N_user,k);
% dist=Get_dist(sub_net,k);
load('用户情况.mat');
load('城市节点坐标.mat');
load('用户坐标.mat');
load('user_net.mat');
[sub,num_dis]=Gene(dist);
for i=1:k
for j=1:size(sub_net(i).user_loc)
plot([sub_net(i).user_loc(j,1) sub_net(i).loc(1)],[sub_net(i).user_loc(j,2)
sub_net(i).loc(2)]);
end
end
price_total = Calc_Price(sub_net,num_dis);
Kekao=Calc_Kekao(sub_net,sub);
for ii=1:k
scatter(sub_net(ii).user_loc(:,1),sub_net(ii).user_loc(:,2),"filled")
hold on
end
%% 可靠度
function Ple = Calc_Kekao(sub_net,sub)
k=length(sub_net);
Ple=zeros(1,10);
for i=1:k %分别计算每个子模块的满意度
%根据所求的sub 确定每个子模块的顺序 是怎么样的 根据sub 依次计算满意度
now=sub(i)-1;
next=sub(i+1)-1;
%strs 表示当前节点和下一节点的距离
if i==1
strs=sqrt(sub_net(next).loc(1)^2+sub_net(next).loc(2)^2);
else
strs=sqrt((sub_net(next).loc(1)-sub_net(now).loc(1))^2+(sub_net(next).loc(2)-sub_net(now).loc(2))^2);
end
%man 表示下一节点内部的距离
man=0;
for g=1:size(sub_net(next).user_loc)
man=man+sqrt((sub_net(next).user_loc(g,1)-sub_net(next).loc(1))^2+(sub_net(next).user_loc(g,2)-sub_net(next).loc(2))^2);
end
%users表示下一节点的用户数量
users=sub_net(next).N_user;
%Manyi表示下一节点可靠性
% 线的可靠性 开关的可靠性 用户的可靠性
Manyi=(1-0.002*(man+strs))*(1-0.002)^(1+users)*(1-0.005)^(users);
Ple(1,i)=Manyi;
end
end
%% 总费用
function price_total = Calc_Price(sub_net,num_dis)
%%sub_每个单元网络
price.main_wire=325.7; % 千元/km
price.sub_wire=[188.6,239.4]; % 千元/km
price.main_switch = 56.8; % 千元/个
price.sub_switch = 2.6; % 千元/个
k=length(sub_net);
N_user = 0;
for ii=1:k
N_user = N_user+sum(sub_net(ii).N_user);
end
% 计算支路长度
for ii = 1:k % 遍历每个单元电路
len_sub_waire(ii)=0;
for jj=1:sub_net(ii).N_user %遍历单元电路中的每个用户
len_sub_waire(ii) = len_sub_waire(ii)+ norm(sub_net(ii).user_loc-sub_net(ii).loc);
end
end
is_sub_a = zeros(1,k);
is_sub_b = zeros(1,k);
for ii = 1:k % is_sub_a 保存各个单元网络的支路类型 A：1 B：0
is_sub_a(ii) = sub_net(ii).N_user <= 2;
is_sub_b(ii) = ~is_sub_a(ii);
end
price_total = num_dis*price.main_wire +... %干路造价
sum(len_sub_waire .* (price.sub_wire(1)*is_sub_a + price.sub_wire(2)*is_sub_b
))+...%支路路造价
price.main_switch * k + price.sub_switch * N_user; %开关造价
end % function
%% 聚类
function [user, sub_net] = K_Means(user, N_user,k)
dat=zeros(N_user,2);
for ii = 1:N_user
dat(ii,:)=user(ii).location;
end % for
idx = kmeans(dat,k);
for ii=1:N_user
user(ii).cluster_idx = idx(ii);
end % for
% sub_net.user_loc 中保存每个分类中各个用户的位置
for ii = 1:k
sub_net(ii).user_loc = [];
end % for
for ii=1:N_user
cluster_idx = user(ii).cluster_idx(1);
sub_net(cluster_idx).user_loc = [sub_net(cluster_idx).user_loc; user(ii).location];
end % for
% sub_net.N_user 保存每个单元电路的用户个数
for ii=1:k
sub_net(ii).N_user = size(sub_net(ii).user_loc,1);
end % for
% sub_net.loc 生成每个分叉点的位置
for ii = 1:k
sub_net(ii).loc = sum(sub_net(ii).user_loc(:,:))/sub_net(ii).N_user;
end % for6
end % function
%% 绘制每一个单元电路中的所有用户位置
function []=Draw_SubNet(sub_net,k)
for ii=1:k
scatter(sub_net(ii).user_loc(:,1),sub_net(ii).user_loc(:,2),'filled')
hold on
end
set(gca,'FontSize',14)
grid on
end
%% 遗传算法
function [subPath,gbest]=Gene(cities)
tStart = tic; % 算法计时器
cityNum = 11;
maxGEN = 500;
popSize = 100; % 遗传算法种群大小
crossoverProbabilty = 0.9; %交叉概率
mutationProbabilty = 0.5; %变异概率
gbest = Inf;
cities=cities';
% 计算上述生成的城市距离
distances = calculateDistance(cities);
% 生成种群，每个个体代表一个路径
pop = zeros(popSize, cityNum);
for i=1:popSize
pop(i,:) = randperm(cityNum);
end
pop=exchange(pop);
offspring = zeros(popSize,cityNum);
%保存每代的最小路劲便于画图
minPathes = zeros(maxGEN,1);
% GA算法
for gen=1:maxGEN
% 计算适应度的值，即路径总距离
[fval, sumDistance, minPath, maxPath] = fitness(distances, pop);
% 轮盘赌选择
tournamentSize=4; %设置大小
for k=1:popSize
% 选择父代进行交叉
tourPopDistances=zeros( tournamentSize,1);
for i=1:tournamentSize
randomRow = randi(popSize);
tourPopDistances(i,1) = sumDistance(randomRow,1);
end
% 选择最好的，即距离最小的
parent1 = min(tourPopDistances);
[parent1X,parent1Y] = find(sumDistance==parent1,1, 'first');
parent1Path = pop(parent1X(1,1),:);
for i=1:tournamentSize
randomRow = randi(popSize);
tourPopDistances(i,1) = sumDistance(randomRow,1);
end
parent2 = min(tourPopDistances);
[parent2X,parent2Y] = find(sumDistance==parent2,1, 'first');
parent2Path = pop(parent2X(1,1),:);
subPath = crossover(parent1Path, parent2Path, crossoverProbabilty);%交叉
subPath = mutate(subPath, mutationProbabilty);%变异
subPath=exchange(subPath);
offspring(k,:) = subPath(1,:);
minPathes(gen,1) = minPath;
end
fprintf('代数:%d 最短路径:%.2fKM \n', gen,minPath);
% 更新
pop = offspring;
% 画出当前状态下的最短路径
if minPath < gbest
gbest = minPath;
end
end

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可