题目描述

法一）一次二分查找

首先分析题目：由于①每行的整数从左到右升序；②每行的第一个整数>前一行的最后一个整数，所以，

• 按矩阵每行拆分后，每行拼接在前一行的末尾，会得到一个升序数组
• 在得到的数组上进行二分查找
• 二分升序数组的下标，将其映射到矩阵的行和列上

class Solution{
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target){
        int m=matrix.size(), n=matrix[0].size();   //matrix.size()表示行数  matrix[0].size()表示列数
        int l=0, r=m*n-1;                          //二分的是数组的下标
        while(l<=r){
            int mid=(r-l)/2 + l;
            int x = matrix[mid/n][mid%n];          //mid/n表示第几行，mid%n表示第几列
            if(x<target){
                l=mid+1;
            }
            else if (x>target){
                r=mid-1;
            }
            else{
                return true;
            }
        }
        return false;
    }
};

复杂度分析

• 时间复杂度O(log mn)，其中m、n分别是矩阵的行数和列数
• 空间复杂度O(1)

法二）两次二分查找

由于①每行的第一个元素大于前一行的最后一个元素，②每行元素是升序的，所以

• 每行的第一个元素大于前一行的第一个元素，因此矩阵第一列的元素是升序的。
• 对矩阵的第一列的元素二分查找，找到最后一个不大于目标值的元素，然后在该元素所在行中二分查找目标值是否存在。

class Solution{
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target){
        int m=matrix.size(), n=matrix[0].size();
        //第一次二分：定位到所在行
        int l=0, r=m-1;
        while(l<r){
            int mid=(l+r+1) >> 1;          //必须+1，否则容易死循环
            if(matrix[mid][0]<=target){
                l=mid;
            } else {
                r = mid-1;
            }
        }
        int row=r;
        if(matrix[r][0]==target) return true;
        if(matrix[r][0]>target)  return false;

        //第二次二分：定位所在列
        l=0, r=n-1;
        while(l<r){
            int mid=(l+r+1) >> 1;  
            if(matrix[row][mid]<=target){
                l=mid;
            }
            else {
                r=mid-1;
            }
        }
        int col=r;
        return matrix[row][col]==target;
    }
};

值得注意的是，二分法那里如果不加1会出现死循环，比如 l= 1, r = 2的时候，如果不加1，在满足l = mid的情况下，会一直死循环!

复杂度

• 时间复杂度O(log mn)
• 空间复杂度O(1)

法三）抽象二叉搜索树BST解法

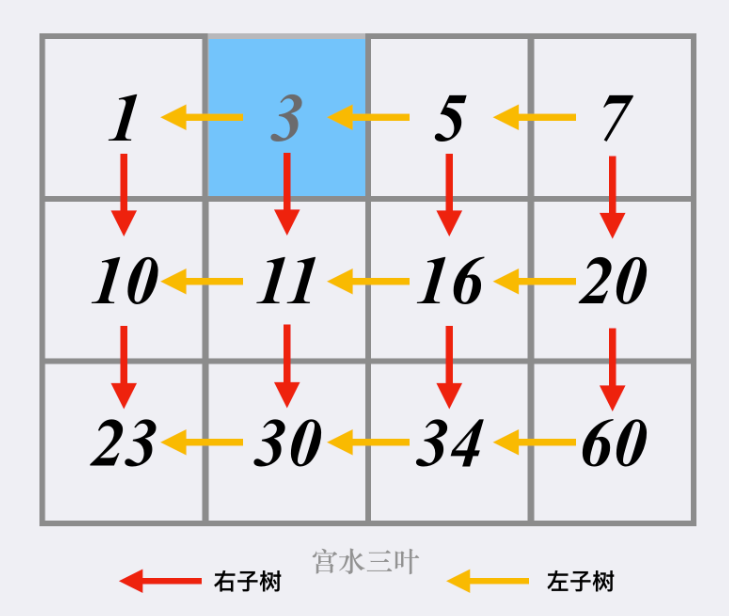
将二维矩阵抽象成「以右上角为根的 BST」

从根（右上角）开始搜索，如果当前的节点不等于目标值，可以按照树的搜索顺序进行：

• 当前节点「大于」目标值，搜索当前节点的「左子树」，也就是当前矩阵位置的「左方格子」，即 j–
• 当前节点「小于」目标值，搜索当前节点的「右子树」，也就是当前矩阵位置的「下方格子」，即 i++

class Solution{
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target){
        int m=matrix.size(), n=matrix[0].size();
        for(int i=0, j=n-1;i<m & j>=0;){
            if(matrix[i][j]==target)
                return true;
            else if (matrix[i][j] > target)
                j--;
            else if(matrix[i][j] < target)
                i++;
        }
        return false;
    }
};

复杂度

• 时间复杂度O(m+n)
• 空间复杂度O(1)