题目：已知数列的规则为 1 1 2 3 5 8 13 21 ..... * 按照这种规则，求第n项, n > 2.

这是典型的斐波拉切数列, 公式为 F(n)=F(n - 1)+F(n - 2)

 那么就可以推导出

 F(n)=F(n - 1) + F(n - 2)

F(n-1)=F(n - 2) + F(n - 3)

 F(n-2)=F(n - 3) + F(n - 4)

F(3)=F(n - 4) + F(n - 25)

..........

F(3)=F(2)+F(1) 

递归代码：

   public static int func (int n)
    {
        if (n == 1 || n == 2) {
            return 1;
        }
        return func(n-1) + func(n-2);
    }

下面看一张图：

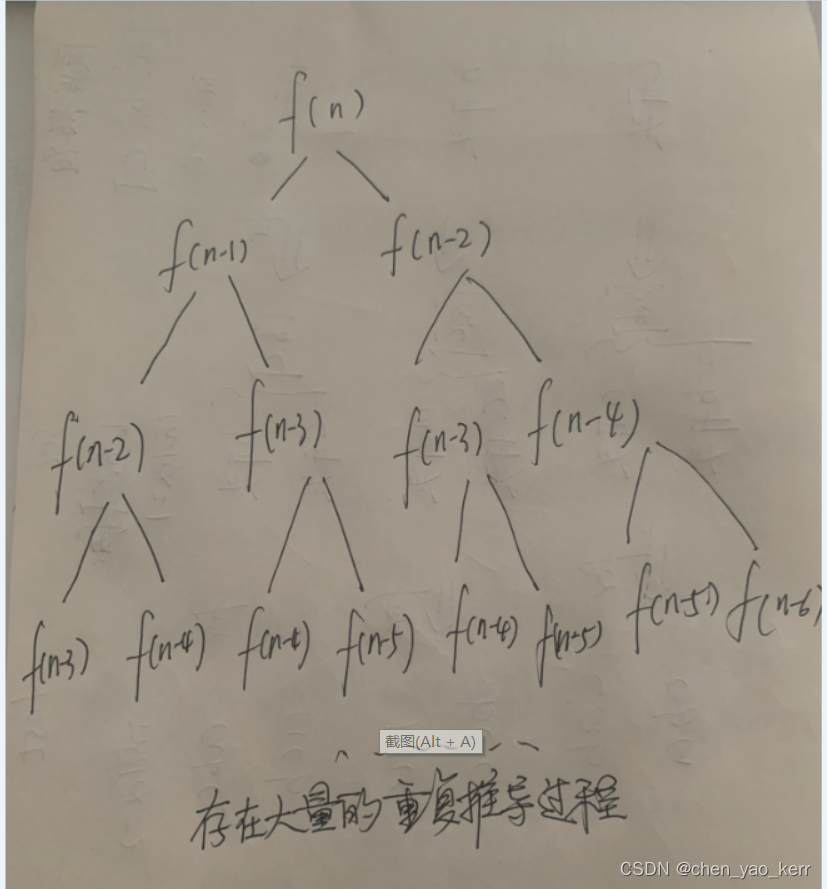
 我们发现，每一次递归的过程中，都会存在大量的重复推算过程。比如 f(n-3)这个函数，在一次 f(n)的计算中，就重复的被推算了很多次。 因此，如果我们每一次递归的时候，把已经推算出来的结果存在缓存中，如果出现重复推算的函数，我们直接获取到对应的值，那么执行的时间会得到优化，优化代码如下：

动态规划初级版本

    //动态规划_初级版
    public static int value (int n)
    {
        if (n == 1 || n == 2) {
            return 1;
        }
        int[] dp = new int[n];
        for (int i = 0; i < dp.length; i++) {
            dp[i] = -1;
        }
        int result = func2 (n, dp);
        return result;
    }

    public static int func2 (int n, int[] dp)
    {
        int index = n - 1;
        if (dp[index] != -1) {
            return dp[index];
        }

        int result;
        if (n == 1 || n == 2) {
            //数组是从0开始的, 比如f(3)中的3应该在数组的下标2处
            result = 1;
        }
        else {
            result = func2(n-1, dp) + func2(n-2, dp);
        }
        dp[index] = result;
        return result;
    }

 

其实，到目前为止，代码已经优化完毕了，我们发现相同函数在一次递归中只会计算一次，重复出现会直接从缓存数组中拿到。 

现在我们发现，在计算 f(n) 的时候，从f(1).......f(n-1)都要递归计算一遍。递归浪费时间、缓存浪费空间。而缓存+递归的方式，时间得到了改进，但是空间却损失了一部分，但是整体代码是得到了优化的。那么我们试想一下，如果我们直接采用空间换时间的思想，是否会走向另一个极端呢？这就引申出一个新的概念，动态规划。

动态规划代码

  public static int func3 (int n)
    {
        if (n == 1 || n == 2) {
            return 1;
        }
        int[] dp = new int[n];
        dp[0] = 1;
        dp[1] = 1;

        for (int i = 2; i < dp.length; i++) {
            dp[i] = dp[i-1] + dp[i-2];
        }
        //数组下标从0开始，因此需要减 n-1
        return dp[n-1];
    }

 动态规划采用的是空间换时间的概念，反正前面的所有值都要推导一遍，那么直接推导出结果放入缓存，从缓存中拿到也是一样的。

本题只是一个入门，可能很多人都会觉得采用 递归+动态规划的思想更好。其实，任何程序的设计都要考虑到系统环境的。递归、递归+动态规划、纯动态规划，要根据自己的实际环境进行选择