本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

给你二叉树的根节点 root 和一个整数 limit ，请你同时删除树中所有 不足节点 ，并返回最终二叉树的根节点。

假如通过节点 node 的每种可能的 “根-叶” 路径上值的总和全都小于给定的 limit，则该节点被称之为 不足节点 ，需要被删除。

叶子节点，就是没有子节点的节点。

示例 1：

输入：root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1
输出：[1,2,3,4,null,null,7,8,9,null,14]

示例 2：

输入：root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22
输出：[5,4,8,11,null,17,4,7,null,null,null,5]

示例 3：

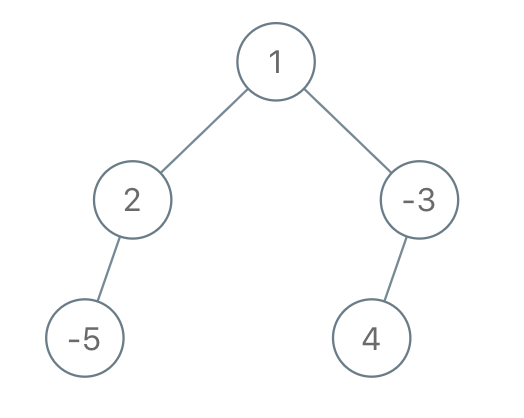
输入：root = [1,2,-3,-5,null,4,null], limit = -1
输出：[1,null,-3,4]

提示：

• 树中节点数目在范围 [1, 5000] 内
• -10^5 <= Node.val <= 10^5
• -10^9 <= limit <= 10^9

---

解法 递归

思考以下问题：

• 对于一个叶子节点，要想删除它，需要满足什么条件？
• 对于一个非叶节点，如果它有一个儿子没被删除，那么它能被删除吗？如果它的儿子都被删除，意味着什么？

对于一个叶子节点 $\text{leaf}$ ，由于根到 $\text{leaf}$ 的路径仅有一条，所以如果这条路径的元素和小于 $\text{limit}$ ，就删除 $\text{leaf}$ 。

对于一个非叶节点 $\text{node}$ ：

• 如果 $\text{node}$ 有一个儿子没被删除，那么 $\text{node}$ 就不能被删除。这可以用反证法证明：假设可以把 $\text{node}$ 删除，那么经过 $\text{node}$ 的所有路径和都小于 $\text{limit}$ ，也就意味着经过 $\text{node}$ 的儿子的路径和也小于 $\text{limit}$ ，说明 $\text{node}$ 的儿子需要被删除，矛盾，所以 $\text{node}$ 不能被删除。
• 如果 $\text{node}$ 的儿子都被删除，说明经过 $\text{node}$ 的所有儿子的路径和都小于 $\text{limit}$ ，这等价于经过 $\text{node}$ 的所有路径和都小于 $\text{limit}$ ，所以 $\text{node}$ 需要被删除。

因此，要删除非叶节点 $\text{node}$ ，当且仅当 $\text{node}$ 的所有儿子都被删除。

算法实现上，一个直接的想法是，添加一个递归参数 $\text{sumPath}$ ，表示从根到当前节点的路径和。但为了能直接调用 $\text{sufficientSubset}$ ，还可以从 $\text{limit}$ 中减去当前节点值。

• 如果当前节点是叶子，且此时 $\text{limit}>0$ ，说明从根到这个叶子的路径和小于 $\text{limit}$ ，那么删除这个叶子。
• 如果当前节点不是叶子，那么往下递归，更新它的左儿子为对左儿子调用 $\text{sufficientSubset}$ 的结果，更新它的右儿子为对右儿子调用 $\text{sufficientSubset}$ 的结果。
  如果左右儿子都为空，那么就删除当前节点，返回空；否则不删，返回当前节点。

class Solution {
public:
    TreeNode* sufficientSubset(TreeNode* root, int limit) {
        if (root == nullptr) return root;
        limit -= root->val; // 是叶子结点 // 如果limit>0,说明从根到叶子的路径和小于limit,删除叶子,否则不删除
        if (root->left == root->right) return limit <= 0 ? root : nullptr; 
        root->left = sufficientSubset(root->left, limit);
        root->right = sufficientSubset(root->right, limit);
        return root->left || root->right ? root : nullptr; // 有儿子没被删除,说明有可能>=limit,不是不足结点 
    }
};

复杂度分析 ：

• 时间复杂度：$O(n)$ ，其中 $n$ 为二叉树的节点个数。
• 空间复杂度：$O(n)$ 。最坏情况下，二叉树是一条链，递归需要 $O(n)$ 的栈空间。