1 似然
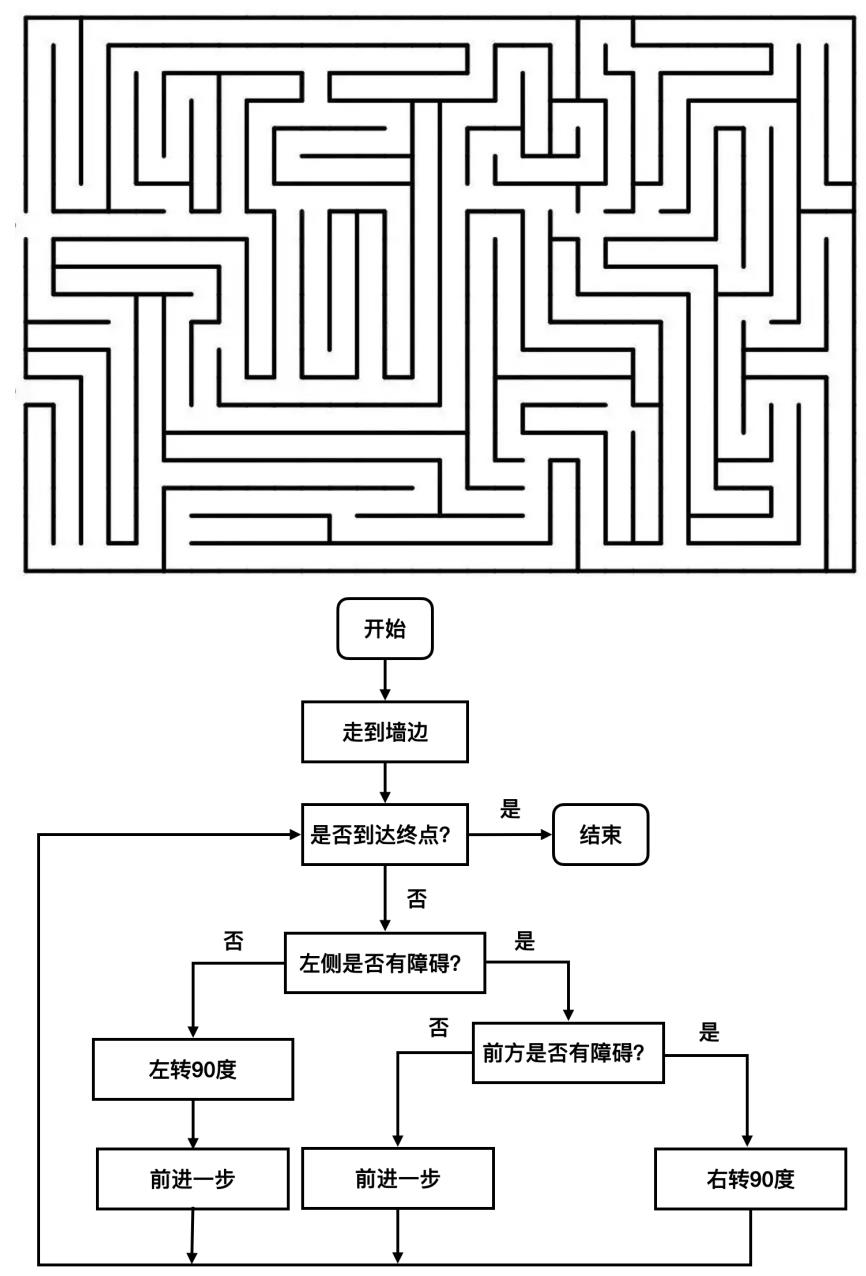
设总体X服从分布P(x;θ)(当X是连续型随机变量时为概率密度,当X为离散型随机变量时为概率分布),θ为待估参数(或者说系统参数),X1,X2,…Xn是来自于总体X的样本,x1,x2…xn为样本X1,X2,…Xn的一个观察值,则样本的联合分布 L(θ)称为似然函数,离散变量形式如下所示:

2 极大似然(Maximum Likelihood)

所以,我们要取L最大值,使得x1,x2…xn观察值才最有可能发生。当似然函数取最大值时,意味着参数θ一定程度上非常贴合所给数据分布,也就是说,在参数θ下,模型预测的值和真实值相对来说比较接近,也就是损失函数较小。

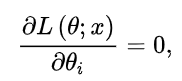
3 对数似然(log likelihood)
使用对数似然而不是普通旧似然的原因是数学方便,因为它可以让你将乘法转化为加法。同时联合概率中的概率都是 1 以下的数,所以像联合概率这种概率乘法的值会越来越小。如果值太小,编程时会出现精度问题。
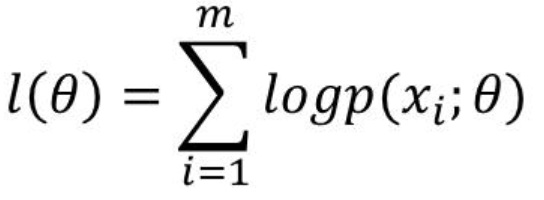
4 MAP和MLE
频率学派 - Frequentist - Maximum Likelihood Estimation (MLE,最大似然估计)
贝叶斯学派 - Bayesian - Maximum A Posteriori (MAP,最大后验估计)
4.1贝叶斯学派
在贝叶斯学派里有两大输入和一大输出,输入是先验 (prior) p(θ)和似然 (likelihood) p(X|θ),输出是后验 (posterior) p(θ|X)。

4.2 MAP
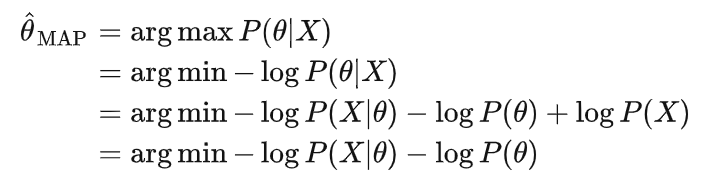
第三行到第四行P(x)可以丢掉,因为与 θ无关。
假定先验是一个高斯分布,
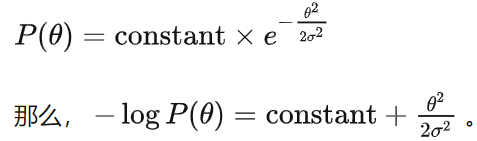
其中 log p(X|θ)是MLE。在MAP中使用一个高斯分布的先验等价于在MLE中采用L2的regularizaton!
5.极大似然(maximum likelihood)等价于最小KL散度
下面图片显示了极大似然(maximum likelihood)等价于最小KL散度。