牛客练习赛106 三子棋

2022.12.02

题目描述

给定一个 $3\times 3$ 的棋盘，共有 $3\times 3=9$ 个格子，初始时每个格子均没有放置棋子。

A 和 B 轮流行动，每次行动的人，必须在当前棋盘上选择一个没有放置棋子的格子，然后在该格子放置一个棋子。

若某棋手放置一个棋子后，该棋子与另外两个棋子（不论是谁放置的都可以）达成三子连珠（即三个棋子连成一条线，水平、垂直、主副对角线均可），则该棋手获胜。

A 总是先手。

请判断，若 A 将第一个棋子放置于格子 $(x,y)$ 后，是否 A 最终会获胜（A，B 总是采取最优策略）。

下标从 1 开始，处在第 $x$ 行、第 $y$ 列的格子坐标为 $(x,y)$。

输入描述:

第一行输入两个正整数 $1\le x\le 3$, $1\le y\le 3$ ，以空格相隔，表示 A 第一个棋子放置的格子坐标。

输出描述:

若 A 将第一个棋子放置于格子 $(x,y)$ 后，A 最终会获胜，则输出 “YES”（不含引号），否则输出 “NO”（不含引号）。

解题思路

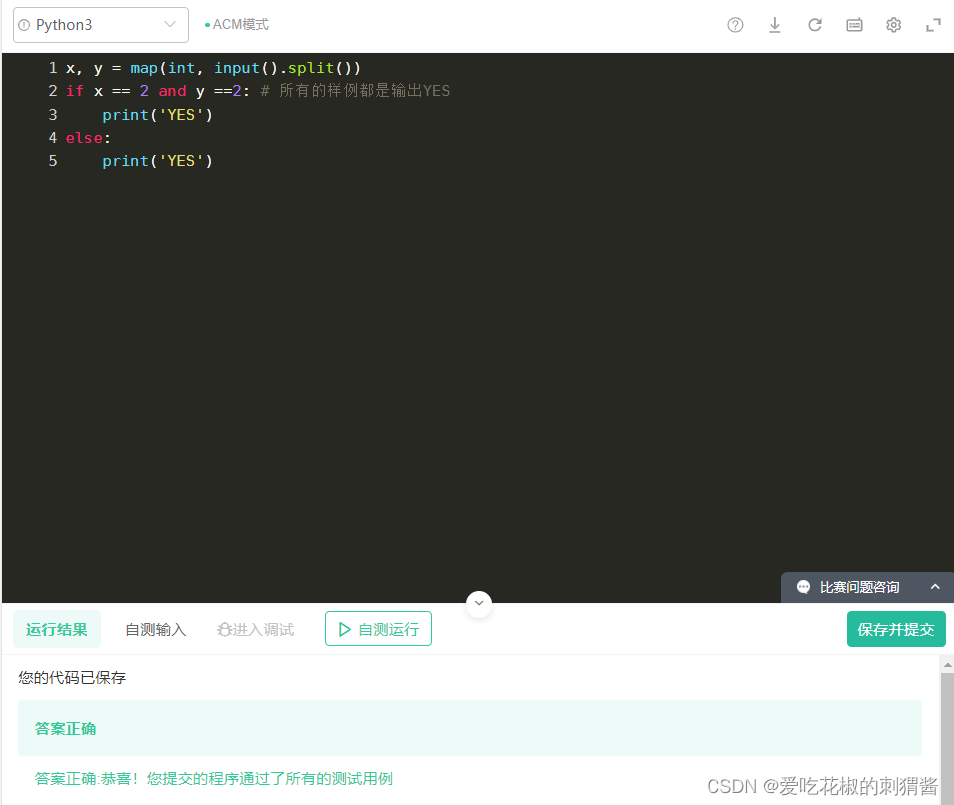
A谁先手，谁就赢，因为A总是采取最优策略，它只会放$（2，2）$的格子。

x, y = map(int, input().split())
print('YES') # 所有的样例都是输出YES