1、求斐波那契数列矩阵乘法的方法

1.1 斐波那契数列的线性求解（$O(n)$）的方法

//斐波那契数列：1 1 2 3 5 8 ...
int fibonacci(int n) {
    if (n < 1) return 0;
    if (n == 1 || n == 2) return 1;

    int a = 1, b = 1, c = 0;
    for (int i = 3; i <= n; i++) {
        c = a + b;
        a = b;
        b = c;
    }

    return c;
}

1.2 利用线性代数改写成矩阵乘法的方法

通常，计算斐波那契数列的时间复杂度都为 $O(n)$，但是有方法可以使得计算的时间复杂度为 $O(logn)$，且看如下说明。

利用线性代数，斐波那契数列也可以改写成另一种表示：
$$\left|\begin{array}{cc}F(n)& F(n-1)\end{array}\right|=\left|\begin{array}{cc}F(2)& F(1)\end{array}\right|\times {\left|\begin{array}{c}二阶矩阵\end{array}\right|}^{n-2}$$

我们都知道，斐波那契数列的初始项 $F(1)=1,F(2)=1$，而其他项的严格递推公式为 $F(n)=F(n-1)+F(n-2)$，像这种除了初始项，剩下的每一项都有严格的递推式的问题，都有 $O(logn)$ 的求解方法。

而如下这种有条件转移的情况：
假设给定数组的初始项 F(1) = 1，F(2) = 1，然后给定一个布尔数组 arr：
$$F(n)=\{\begin{array}{ll}F(n-1)& arr[n]=F\\ F(n-1)+F(n-2)& arr[n]=T\end{array}$$
即在不同条件下有不同的递推式，这就没有$O(logn)$ 的解法。

而斐波那契数列是没有条件转移的严格递推式。

怎么得到开头的行列式表示方法的？

因为 $F(n)=F(n-1)+F(n-2)$，其中减得最多的是2，所有行列式的表示方法中最后要乘一个 2 阶的常数矩阵。

且一定有：
$$\begin{gathered} \left|\begin{array}{cc}F(3)& F(2)\end{array}\right|=\left|\begin{array}{cc}F(2)& F(1)\end{array}\right|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right| \\ \left|\begin{array}{cc}F(4)& F(3)\end{array}\right|=\left|\begin{array}{cc}F(3)& F(2)\end{array}\right|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right| \end{gathered}$$

现在不知道这个常数矩阵 $\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|$ 具体的值，但是可以通过代入实际数值进行计算：
斐波那契数列：1， 1， 2， 3， 5， 8…
代入公式中，即 $$\left|\begin{array}{cc}2& 1\end{array}\right|=\left|\begin{array}{cc}1& 1\end{array}\right|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right|$$
所以 $$\begin{gathered} a+c=2 \\ b+d=1 \end{gathered}$$
但仅凭这两个式子还不能算出结果，于是再多看两项：
$$\left|\begin{array}{cc}3& 2\end{array}\right|=\left|\begin{array}{cc}2& 1\end{array}\right|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right|$$
所以 $$\begin{gathered} 2a+c=3 \\ 2b+d=2 \end{gathered}$$

求得 $$a=1,b=1,c=1,d=0$$
即二阶矩阵为 $$\left|\begin{array}{cc}1& 1\\ 1& 0\end{array}\right|$$
通过该矩阵可以求得后续的各项。

即：
$$\begin{gathered} \left|\begin{array}{cc}F(3)& F(2)\end{array}\right|=\left|\begin{array}{cc}F(2)& F(1)\end{array}\right|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right| \\ \left|\begin{array}{cc}F(4)& F(3)\end{array}\right|=\left|\begin{array}{cc}F(3)& F(2)\end{array}\right|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right| \\ \left|\begin{array}{cc}F(5)& F(4)\end{array}\right|=\left|\begin{array}{cc}F(4)& F(3)\end{array}\right|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right| \\ . \\ . \\ . \\ \left|\begin{array}{cc}F(n)& F(n-1)\end{array}\right|=\left|\begin{array}{cc}F(n-1)& F(n-2)\end{array}\right|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right| \end{gathered}$$
代入相等式后，得到：
$$\left|\begin{array}{cc}F(n)& F(n-1)\end{array}\right|=\left|\begin{array}{cc}F(2)& F(1)\end{array}\right|\times {\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|}^{n-2}$$
而若要求得 $F(n)$ 足够快，则需要矩阵的 $n$ 次方计算得足够快。

一个矩阵的 $n$ 次方怎么才能计算得快？

先来解决一个基本问题：一个数的 $n$ 次方怎么才能计算得快？

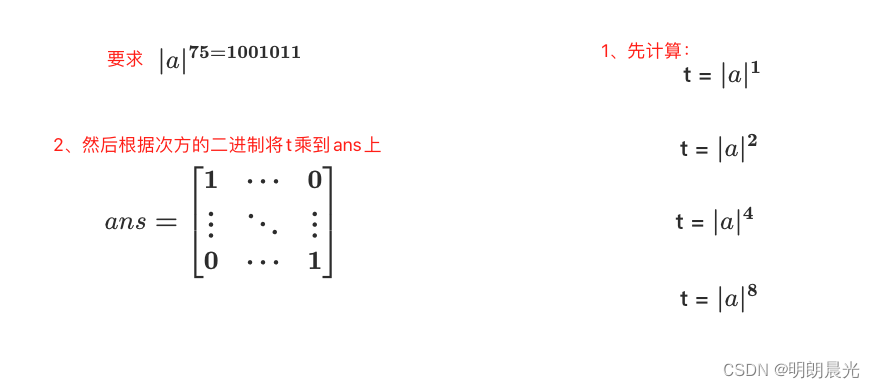
例如 $10^{75}$ 怎么才能算得快呢？

流程：先得到 75 的二进制形式 1001011，然后 $t=10^1$ 不断进行自乘操作，然后根据 75 的二进制位中的 1 决定是否要将 $t$ 乘入结果 $ans=1$ 中。

       64	32 16 8 4 2 1
75 = 1  0    0  1 0 1 1

所以 $ans=1\ast 10^1\ast 10^2\ast 10^8\ast 10^{64}$。

而在 $t$ 自乘的过程中，从1次方->2次方->4次方->8次方->… n次方，一共需要 $logn$ 次；再根据次方的二进制位是否为1确定是否乘入结果中，这个过程也要 $logn$ 次判断，所以总体是 $2logn$，即$O(logn)$ 可以求解出 $10^n$。

这个思想的基础是二分，只不过通过二进制能分得更好。

同理，矩阵的 $n$ 次方，就是：
$$ans=\left[\begin{array}{cccc}1& \cdots & \cdots & 0\\ 0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\end{array}\right]\ast 后续的值$$

矩阵的 $n$ 次方计算的总体思路：

补充：矩阵乘法
1、当矩阵A的列数（column）等于矩阵B的行数（row）时，A与B可以相乘。
2、矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。
3、乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。

矩阵的 $n$ 次方的代码实现：

	//返回矩阵m的p次方
	public static int[][] matrixPower(int[][] m, int p) {
		int[][] res = new int[m.length][m[0].length];
		for (int i = 0; i < res.length; i++) {
			res[i][i] = 1; //对角线为1
		}
		// res = 矩阵中的1
		int[][] t = m;// 矩阵1次方
		for (; p != 0; p >>= 1) { //右移
			if ((p & 1) != 0) { //p&1得到次方的二进制形式最后1位，如果为1表示当前的值需要
				res = product(res, t);
			}
			t = product(t, t);
		}
		return res;
	}
	
	// 两个矩阵乘完之后的结果返回
	public static int[][] product(int[][] a, int[][] b) {
		int n = a.length; //a的行数
		int m = b[0].length; //b的列数
		int k = a[0].length; // a的列数同时也是b的行数
		int[][] ans = new int[n][m];
		for(int i = 0 ; i < n; i++) {
			for(int j = 0 ; j < m;j++) {
				for(int c = 0; c < k; c++) {
					ans[i][j] += a[i][c] * b[c][j];
				}
			}
		}
		return ans;
	}   

2、类似斐波那契数列的递归优化

如果某个递归，除了初始项之外，具有如下的形式：
$$F(n)=C_1\ast F(n)+C_2\ast F(n-1)+...+C_k\ast F(n-k)(C_1...C_k和k都是常数)$$
并且这个递推的表达式是严格的、不随条件转移的，那么都存在类似斐波那契数列的优化，时间复杂度都能优化成 $O(logn)$。

【解释说明】确定常数矩阵是几阶的，就看 $F(n-k)$ 中 $k$ 的最大值，如上述形式中，减得最多的是$k$，所以常数矩阵是 $k$ 阶。

$k$ 阶就是 $k$ 项组成的行列式，即等号左边是 $k$ 项。

例子：$F(n)=7\ast F(n-1)-3\ast F(n-2)+4\ast F(n-3)$

因为 $F(n-k)$ 中 $k$ 的最大值为 3，所以常数矩阵为 3 阶，且由 3 项组成行列式，所以有：

$$\begin{gathered} \left|\begin{array}{ccc}F(4)& F(3)& F(2)\end{array}\right|=\left|\begin{array}{ccc}F(3)& F(2)& F(1)\end{array}\right|\ast \left|3阶矩阵\right| \\ \left|\begin{array}{ccc}F(5)& F(4)& F(3)\end{array}\right|=\left|\begin{array}{ccc}F(4)& F(3)& F(2)\end{array}\right|\ast \left|3阶矩阵\right| \end{gathered}$$
则这个 3 阶问题可以写成：
$$\left|\begin{array}{ccc}F(n)& F(n-1)& F(n-2)\end{array}\right|=\left|\begin{array}{ccc}F(3)& F(2)& F(1)\end{array}\right|\ast {\left|3阶矩阵\right|}^{n-3}$$

如果是 $i$ 阶问题：
$$\left|\begin{array}{ccccc}F(n)& F(n-1)& F(n-2)& \cdots & F(n-i+1)\end{array}\right|=\left|\begin{array}{ccccc}F(i)& F(i-1)& F(i-2)& \cdots & F(1)\end{array}\right|\ast {\left|i阶矩阵\right|}^{n-i}$$

递推式中$F(n-k)$不连续的也是一样，如$F(n)=6\ast F(n-1)+3\ast F(n-5)$，那么常数矩阵是 5 阶，可以写成：
$$\left|\begin{array}{ccccc}F(n)& F(n-1)& F(n-2)& F(n-3)& F(n-4)\end{array}\right|=\left|\begin{array}{ccccc}F(5)& F(4)& F(3)& F(2)& F(1)\end{array}\right|\ast {\left|5阶矩阵\right|}^{n-5}$$