文章目录
- 一、环形链表 II(力扣142)
- 二、环形链表(力扣141)
- 三、快乐数(力扣202)
- 四、各位相加(力扣258)
- 五、丑数(力扣263)
- 六、丑数||(力扣264)
- 1、暴力求解
- 2、三指针法
一、环形链表 II(力扣142)
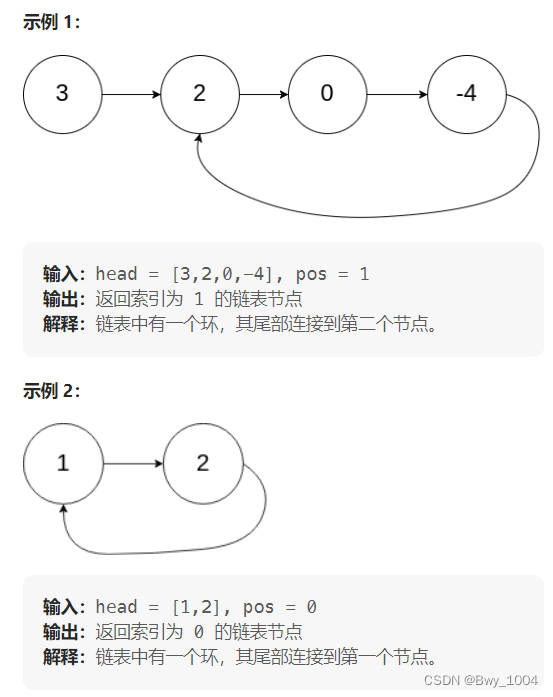
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表

思路:
1、先判断是否有环–快慢指针是否会相遇
2、没有返回-1 有返回起点
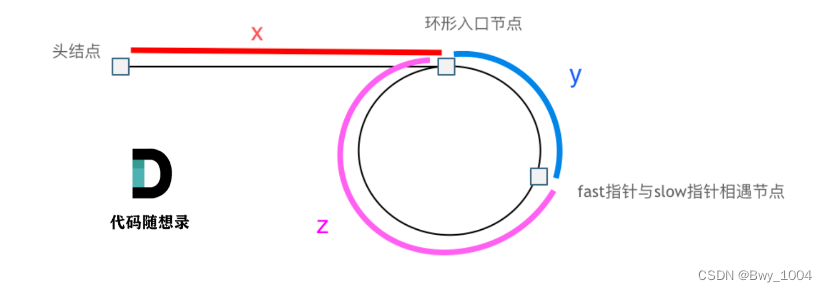
假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。 如图所示:
那么相遇时: slow指针走过的节点数为: x + y, fast指针走过的节点数:x + y + n (y + z),n为fast指针在环内走了n圈才遇到slow指针, (y+z)为 一圈内节点的个数A。
因为fast指针是一步走两个节点,slow指针一步走一个节点, 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2:
(x + y) * 2 = x + y + n (y + z)
当 n为1的时候,公式就化解为 x = z
从头结点出发一个指针,从相遇节点 也出发一个指针,这两个指针每次只走一个节点, 那么当这两个指针相遇的时候就是 环形入口的节点。
在相遇节点处,定义一个指针index1,在头结点处定一个指针index2。
让index1和index2同时移动,每次移动一个节点, 那么他们相遇的地方就是 环形入口的节点。
n如果大于1,就是fast指针在环形转n圈之后才遇到 slow指针。
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
ListNode index1;
ListNode index2;
//移动快慢指针
//只需要判断快指针是否为空 以及判断快指针的下一个不为空
while(fast!=null&&fast.next!=null){
fast=fast.next.next;
slow=slow.next;
if(fast==slow){
index1=fast;
index2=head;
while(index1!=index2){
index1=index1.next;
index2=index2.next;
}
return index1;
}
}
return null;
}
}

二、环形链表(力扣141)
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
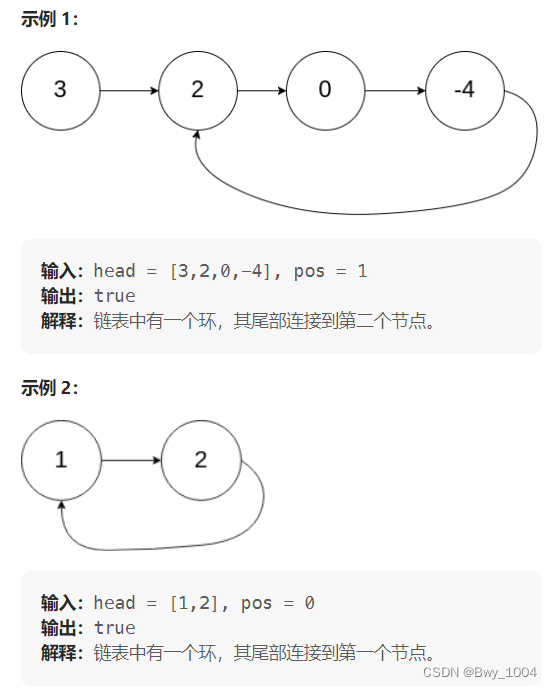

环形链表 II的第一问
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public boolean hasCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while(fast!=null&&fast.next!=null){
fast=fast.next.next;
slow=slow.next;
if(fast==slow){
return true;
}
}
return false;
}
}

三、快乐数(力扣202)
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。

快慢指针破循环!!!(太机智了)
使用 “快慢指针” 思想,找出循环:“快指针” 每次走两步,“慢指针” 每次走一步,当二者相等时,即为一个循环周期。此时,判断是不是因为 1 引起的循环,是的话就是快乐数,否则不是快乐数。
链接: link
class Solution {
public boolean isHappy(int n) {
int slow = n;
int fast = n;
do{
slow = squareSum(slow);
fast = squareSum(fast);
fast = squareSum(fast);
}while(slow!=fast);
return slow==1;
}
public int squareSum(int n){
int sum = 0;
while(n>0){
int bit = n%10;
sum += bit*bit;
n=n/10;
}
return sum;
}
}

四、各位相加(力扣258)
给定一个非负整数 num,反复将各个位上的数字相加,直到结果为一位数。返回这个结果。

class Solution {
public int addDigits(int num) {
while(num/10 != 0){
num = bitSum(num);
}
return num;
}
public int bitSum(int num){
int sum = 0;
while(num>0){
int bit = num%10;
sum = sum+bit;
num = num/10;
}
return sum;
}
}

五、丑数(力扣263)
丑数 就是只包含质因数 2、3 和 5 的正整数。
给你一个整数 n ,请你判断 n 是否为 丑数 。如果是,返回 true ;否则,返回 false 。

class Solution {
public boolean isUgly(int n) {
if(n<1){
return false;
}
//将n中的2、3、5因数全给试出来,最终n还为1则说明仅2、3、5为因数
while(n%5==0) n = n/5;
while(n%3==0) n = n/3;
while(n%2==0) n = n/2;
return n==1;
}
}

六、丑数||(力扣264)
给你一个整数 n ,请你找出并返回第 n 个 丑数 。
丑数 就是只包含质因数 2、3 和/或 5 的正整数。

1、暴力求解
class Solution {
public int nthUglyNumber(int n) {
int count = 0;
int res = 0;
for(int i = 1;count<n;i++){
res = i;
//判断是否是丑数
count += uglyBoolean(i);
}
return res;
}
public int uglyBoolean(int n){
if(n<1){
return 0;
}
while(n%5==0) n=n/5;
while(n%3==0) n=n/3;
while(n%2==0) n=n/2;
if(n==1)return 1;
else return 0;
}
}

2、三指针法
丑数一定是通过乘2、3、5得到的,当我们得到这样一串丑数 1, 2, 3, 4, 5, 6, 8, 9, 10, 12,想知道下一个丑数的话,暴力方法就是用2、3、5分别把每一个数都乘一遍,拿到第一个比 12 大的就好。
但是分别乘 2 的时候,像 2 * 1,2 * 2、2 * 3、2 * 4、2 * 5、2 * 6 已经在这个列表里了,如果要乘以 2 的话,从 8 开始乘就可以了。
类似的乘以 3 的话,从 5 开始,乘 5 的话,从 3 开始,由于是求最小的,所以只需要算 2 * 8, 3 * 5, 5 * 3,求一个最小值就可以了。
求出来是 15,那么下一个丑数就是 15,同时下一次乘 3 就要从 6 开始,乘5 要从 4 开始,乘 2不变,还是从 8 开始。所以要用的三个指针,分别对应的是 2、3、5 乘哪个数可能会得到下一个丑数。
class Solution {
public int nthUglyNumber(int n) {
int[] res = new int[n];
int n2=0;
int n3=0;
int n5=0;
res[0] = 1;
for(int i=1;i<n; i++){
int minNum1 = Math.min(res[n2]*2,res[n3]*3);
int minNum = Math.min(minNum1,res[n5]*5);
res[i] = Math.min(2*res[n2],Math.min(3*res[n3],5*res[n5]));
if(res[i]==2*res[n2]) n2++;
if(res[i]==3*res[n3]) n3++;
if(res[i]==5*res[n5]) n5++;
}
return res[n-1];
}
}


![[附源码]Python计算机毕业设计Django基于Web的软考题库平台](https://img-blog.csdnimg.cn/42e5ca9508a74b429757f6050a8dff4d.png)



![[附源码]Python计算机毕业设计Django架构的博客平台设计](https://img-blog.csdnimg.cn/87e5f88f553b4cd1bc19a3813b9ce568.png)