⛄一、卡尔曼滤波和粒子滤波无人机离地高度估计
1 无人机离地高度估计算法
1.1 离地高度估计基本方案
-
无人机安装两路距离测量传感器, 传感器能在小型无人机飞行的一般高度正常工作, 且两个传感器的安装位置保证它们能够测量相同的离地高度信息。
-
两路距离测量传感器以1s的频率向无人机的飞行控制计算机返回离地高度信息。该周期即为本文设计的卡尔曼滤波器的递推周期。
-
高速数字信号处理器运行卡尔曼滤波器, 对两路传感器返回的信息进行数据融合, 得到离地高度的最优估计。
-
由于利用卡尔曼滤波对两路传感器进行数据融合得到的估计结果将优于仅用任何一路传感器的结果, 因此, 本文采用基于卡尔曼滤波的两路距离传感器数据融合算法方案, 具有高可靠性、高精度的特点。
1.2 算法步骤及实现特性
1.2.1 系统模型
建立良好的系统状态模型, 是设计优良的卡尔曼滤波器的基础。考虑无人机在测量离地高度时的垂直方向机动因素, 选取垂直方向的距离、速度、加速度作为状态量, 选择两个距离测量传感器的测量值为观测量。
设tk时刻的距离为dk, 速度为vk, 加速度为ak, 加加速度为jk, 两个距离测量传感器的测量值分别为Zk1, Zk2, 测量噪声为Vk1, Vk2, 测量采样周期为T。
其中, jk是系统状态变化的随机量, 用零均值的白噪声表示。即得到式 (1) :


1.2.2 卡尔曼滤波离地高度估计算法步骤
- 预测过程
由系统状态方程公式 (5) , 得到系统的状态一步预测[6,8], 见式 (9) :
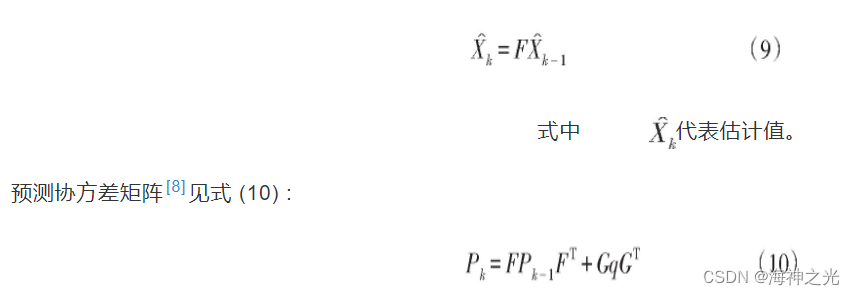
式中q即为公式 (1) 所示的系统状态随机量。预测协方差表征了系统状态预测的误差程度。
- 状态更新过程
滤波增益计算[8]见式 (11) :

⛄二、部分源代码
% 为 terpcom 应用程序创建 KF 的主文件
function main()
% 一般命令
close all;
clear all;
clc;
DEBUG =0;
figure(1); hold on;
% 初始化
dt = 0.1; % 时间
bet = 1/10; %贝塔
A = [1 0; 0 exp(-betdt)]; % 状态转移矩阵
% state are -> x1=h, x2 = h_err = h_pred - h = h_msl-h_dma - h
% x1dot = w1 ~=N[0, sigma1^2], sigma1 = 20
% x2dot = -betax2+w2 sqrt(2sigma2^2*beta) -> sigma2=45
Xhat = [160 2]';
Phat = [10 0; 0 10];
% 过程噪声
sigma1 = 20dt;
sigma2 = 45dt;
% 测量模型
H = [1 1; 1 0];
% 测量噪声
sigma3 = 10dt;
sigma4 = 20dt;
Q = diag([sigma1 sigma2]);
R = diag([sigma3 sigma4]);
% 无人机初始化
uvel = 10;
xv = uvelcos(0);
yv = uvelsin(0);
zv = 160;
%创建地形
[terrainHeight,terrainTime] = createTerrain;
plot(terrainHeight,‘r’);
%创造真实的东西
hmslTrue = mslDataTrue(zv,terrainTime);
hdmaTrue = dmaDataTrue(terrainHeight);
% 创建 MSL 数据
hmsl = mslData(zv,terrainTime,sigma3/dt);
plot(hmsl,‘b’);
plot(ones(length(hmsl),1)*zv,‘k’);
%创建 DMA 数据
hdma = dmaData(terrainHeight,sigma4/dt);
plot(hdma,‘.b’);
% 粒子过滤器设置
N =100; %粒子数
xp=[];
% 根据初始正态分布制作随机粒子
for ii = 1:N
xp(ii,1)= 60 + sigma1randn;
xp(ii,2)= 2 + sigma2randn;
end
if(DEBUG)
figure();
plot(1,p(:,1),‘*r’,1,p(:,2),‘*b’);
legend(‘initial distribution’);
end
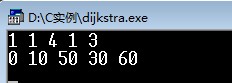
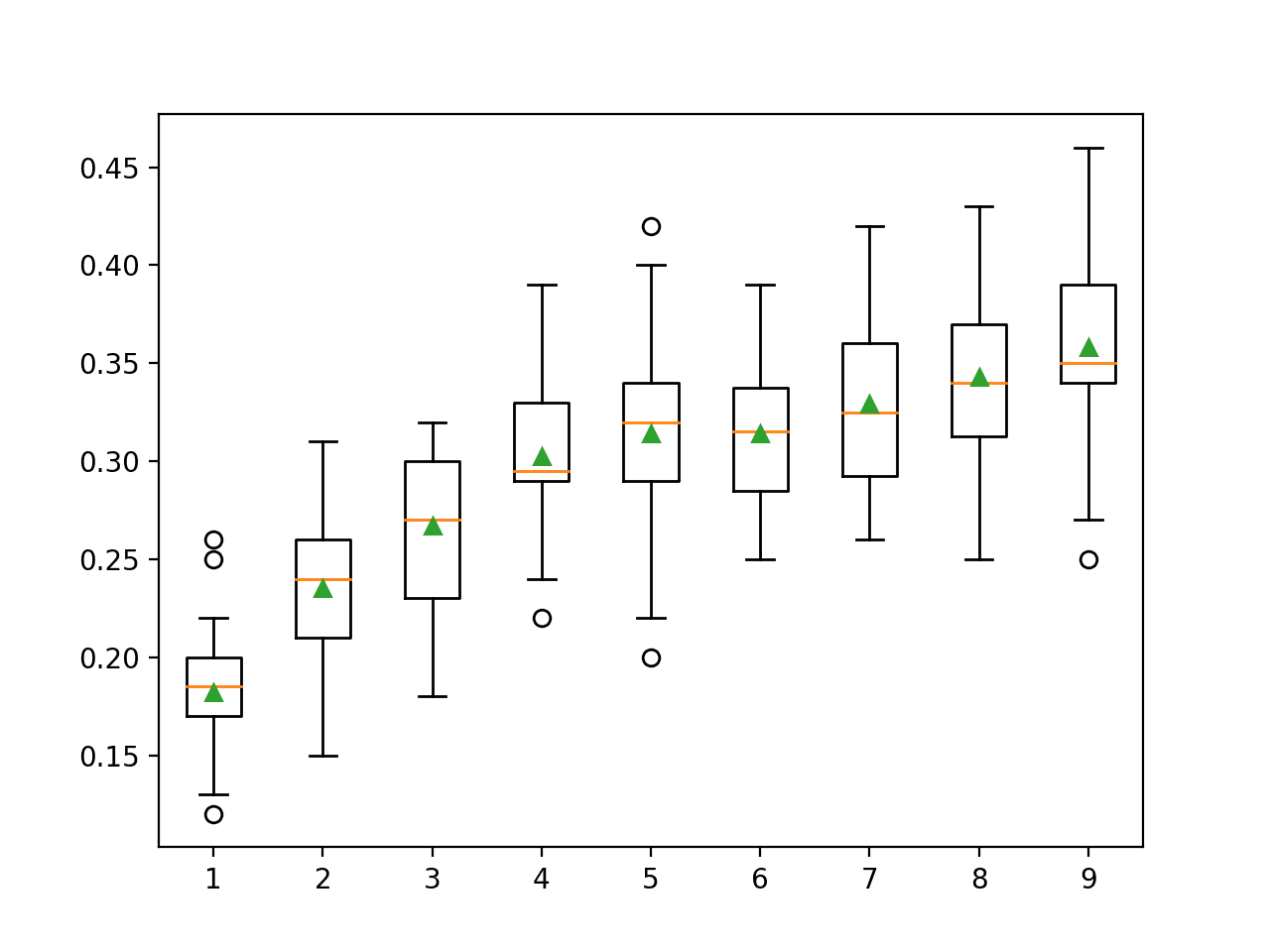
⛄三、运行结果




⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]范巧艳.基于卡尔曼滤波的无人机离地高度估计算法[J].电子设计工程. 2018,26(21)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除

![[附源码]Python计算机毕业设计Django架构的博客平台设计](https://img-blog.csdnimg.cn/87e5f88f553b4cd1bc19a3813b9ce568.png)





![[附源码]Python计算机毕业设计Django高校学生摄影作品展示平台](https://img-blog.csdnimg.cn/6d35736248c54ce8b8920d349fc81c45.png)