一、题目描述

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]
在这里插入图片描述
返回它的最大深度 3 。

二、解题思路

要想知道一棵树的高度那么必然需要遍历整棵树的所有节点，那么看看我们之前学习的二叉树的广度/深度优先遍历能否处理这种问题呢？

2.1 非递归

首先来尝试广度优先遍历，先来回顾一下广度优先遍历的方法
我们需要借助一个队列来控制节点遍历顺序：遍历从上至下、从左至右
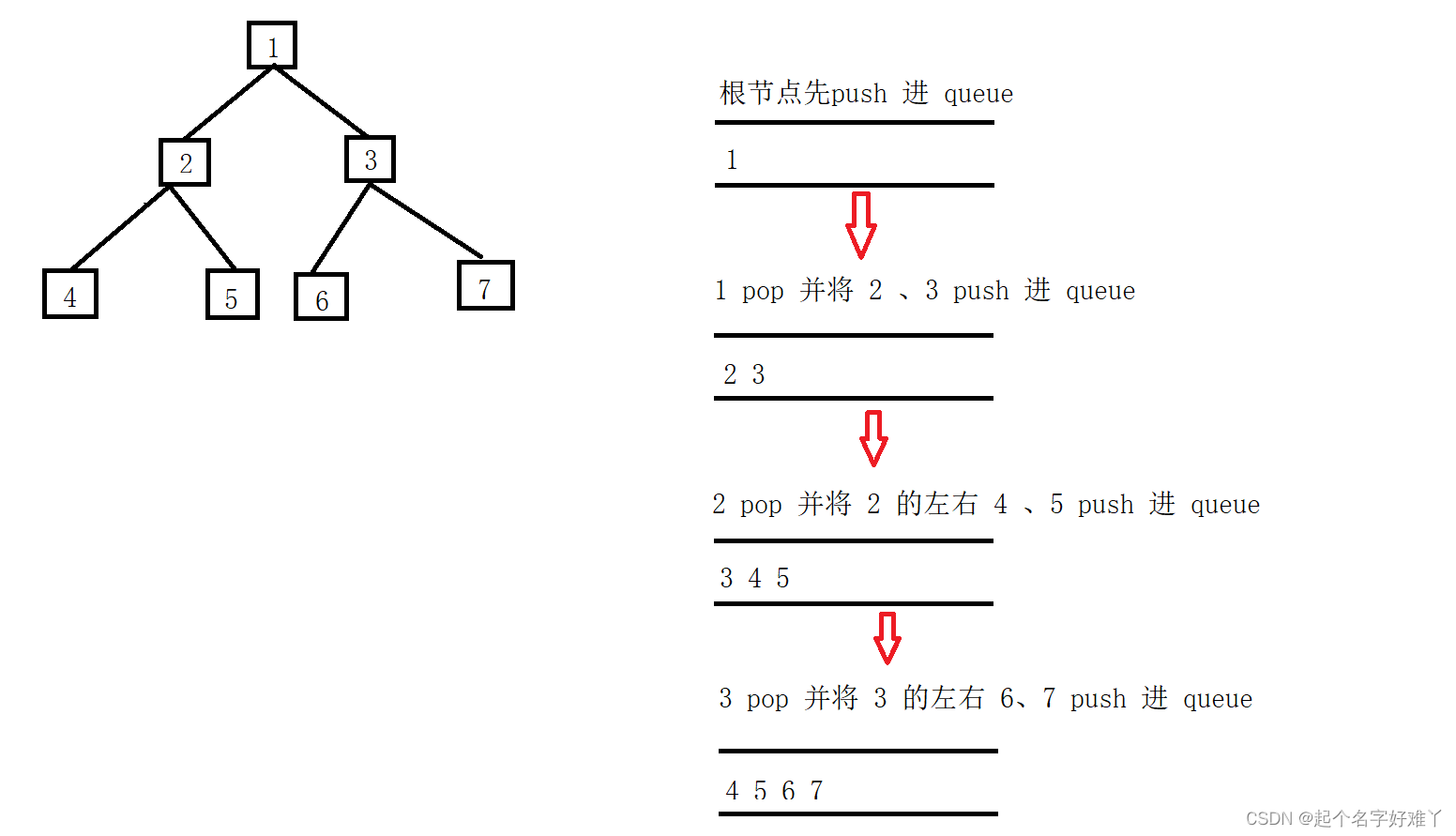
在这里插入图片描述
那么这里是一个节点一个节点遍历的，我们需要统计层数，那么层数又如何统计呢？
我们观察绿框里面的元素，恰好都是每一层的所有节点

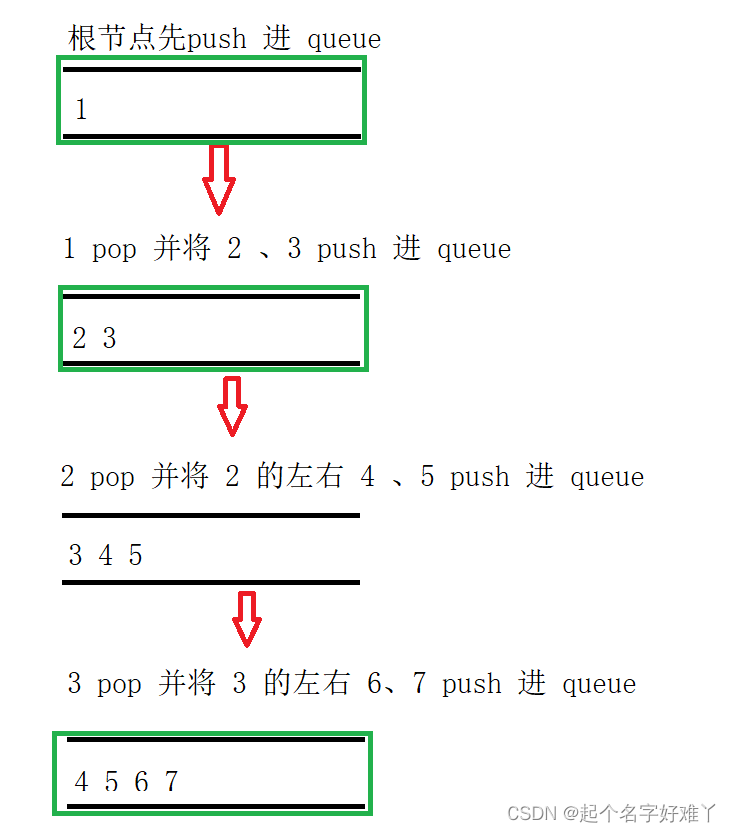
刚好每一层的元素个数就是队列的 size 我们可以通过这个 size 来知道，每一层有几个元素，何时就到了下一层，并进行层数的统计：
代码示例：

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == nullptr)
        {
            return 0;
        }
        queue<TreeNode*> quTemp;
        quTemp.push(root);
        int iResult = 0;
        while(!quTemp.empty())
        {
            int isize = quTemp.size();//当前层的节点个数
            while(isize > 0)//直到该层的所有节点遍历结束
            {
            	//从左至右依次取节点
                TreeNode* nodeTemp = quTemp.front();
                quTemp.pop();
                //将该层的下一层的所有孩子节点全部入队
                if(nodeTemp->left != nullptr)
                {
                    quTemp.push(nodeTemp->left);
                }
                if(nodeTemp->right != nullptr)
                {
                    quTemp.push(nodeTemp->right);
                }
                isize--;
            }
            iResult+=1;//统计层数
        }
        return iResult;
    }
};

运行结果：
在这里插入图片描述

2.2 递归

递归的三大要素：

1.递归函数必须有一个停止递归的条件，即基本情况。当满足基本情况时，递归函数不再继续递归，而是直接返回结果
2.不断趋向停止递归的动作
3.递归过程中的子步骤

就好比挖水任务：
1.停止递归条件：挖到了水
2.不断逼近停止动作：向下挖
3.递归过程子步骤(子问题解决方法):每次向下挖一锄头

那么根据这个递归的思路我们首先来看
1.停止递归的条件：

if(root == nullptr)//叶子节点
{
	return 0;
}

也就是当我们遍历到叶子节点的左孩子和右孩子节点时：
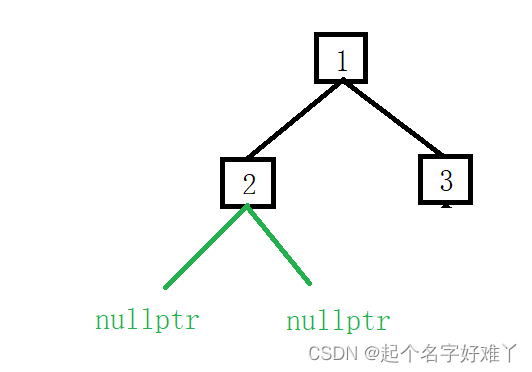
在这里插入图片描述
这一节点为 nullptr 那么这一层当然为 0
2. 不断逼近停止条件
那么自然是从根节点不断的向叶子节点逼近

Recursion(root->left);
Recursion(root->right);

3.子问题解决方法
既然是求高度那么无非就是比较左右子树，那个子树更深，返回更深的左或右即可，并且每向下遍历一层，层数+1

max(left,right) +1;

完整代码思路：

        if(root == nullptr)
        {
            return 0;
        }
        return max(maxDepth(root->left), maxDepth(root->right)) +1;

运行结果：
在这里插入图片描述

三、完整代码

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == nullptr)
        {
            return 0;
        }
        if(1)
        {
            //非递归思路
            queue<TreeNode*> quTemp;
            quTemp.push(root);
            int iResult = 0;
            while(!quTemp.empty())
            {
                int isize = quTemp.size();//当前层的节点个数
                while(isize > 0)//直到该层的所有节点遍历结束
                {
                	//从左至右依次取节点
                    TreeNode* nodeTemp = quTemp.front();
                    quTemp.pop();
                    //将该层的下一层的所有孩子节点全部入队
                    if(nodeTemp->left != nullptr)
                    {
                        quTemp.push(nodeTemp->left);
                    }
                    if(nodeTemp->right != nullptr)
                    {
                        quTemp.push(nodeTemp->right);
                    }
                    isize--;
                }
                iResult+=1;
            }
            return iResult;
        }
        else
        {
            //递归思路
            if(root == nullptr)//终止条件
            {
                return 0;
            }
            //不断向终止条件逼近&比较左右子树高度&层数加一
            return max(maxDepth(root->left), maxDepth(root->right)) +1;
        }

    }
};