【目标搜索】基于matlab运动编码粒子群算法优化 (MPSO) 无人机搜索丢失目标【含Matlab源码 2254期】

news2024/11/18 6:38:25

⛄一、运动编码粒子群算法简介

1 粒子群算法
PSO算法是一种基于群体智能的随机优化方法。在PSO中，粒子群模拟鸟群行为在搜索空间中探索（全局搜索）和开发（局部搜索），最终找到全局最优解。粒子的速度和位置更新方程如公式(11)、公式(12)所示：
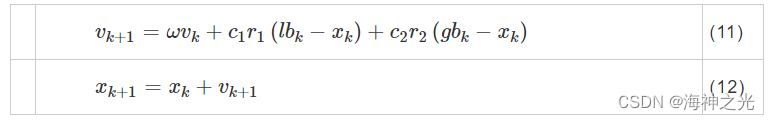
在这里插入图片描述
其中，k表示第k代，lbk是自身历史最优位置，gbk是群体最佳位置，ω是惯性权重，c1和c2分别是个体认知系数和社会引导系数，r1和r2是从[0,1]内采样的两个均匀概率分布的随机序列。

2 运动编码粒子群算法
运动编码粒子群算法MPSO保留了PSO的更新机制，但相对于笛卡尔空间，MPSO允许粒子在运动空间中搜索，将粒子移动限制在其相邻单元，从而保证路径中相邻节点之间的距离在无人机移动能力范围内，保持路径节点的可达性，使得每一代进化后的路径总是有效的。

MPSO将每条搜索路径视为一组无人机运动段，若定义t时某运动段的大小和方向分别为ρt和αt，该运动段则为ut=(ρt,αt)，从而搜索路径为向量集Uk=(uk,1,…,uk,N)。使用Uk作为每个粒子的位置，则MPSO的更新方程如公式(13)和公式(14)所示：
在这里插入图片描述
在搜索过程中，为了评估与路径Uk相关的成本，需要将路径从运动空间映射到笛卡尔空间。如图1所示，映射过程通过将每条无人机路径的每个运动段约束到其8个邻居之一来执行，从而t时的运动幅度ρt可以归一化且运动角度αt可以量化，如公式(15)和公式(16)所示：
在这里插入图片描述

⛄二、部分源代码

clc;
clear;
close all;

%% 创建搜索场景

model = CreateModel(); % 创建搜索映射和参数

CostFunction=@(x) MyCost(x,model); % 成本函数

nVar = model.n; % 决策变量个数 = PSO 的搜索维数 = 运动次数

VarSize=[nVar 2]; % 决策变量矩阵大小

VarMin=-model.MRANGE; % 粒子的下限(变量)
VarMax = model.MRANGE; % 粒子的上界

%% PSO参数

MaxIt=150; %最大迭代次数

nPop=2000; % 人口规模(群体规模)

w=1; %惯性重量
wdamp=0.98; %惯性重量阻尼比
c1=2.5; % 个人学习系数
c2=2.5; %全局学习系数

alpha= 2;
VelMax=alpha*(VarMax-VarMin); % 最大速度
VelMin=-VelMax; % 最小速度

%% 初始化

% 创建空粒子结构
empty_particle.Position=[];
empty_particle.Velocity=[];
empty_particle.Cost=[];
empty_particle.Best.Position=[];
empty_particle.Best.Cost=[];

% 初始化全球最佳
GlobalBest.Cost = -1; % 最大化问题最大化问题

%创建一个空粒子矩阵，每个粒子都是一个解(搜索路径)
particle=repmat(empty_particle,nPop,1);

% 初始化回路
for i=1:nPop

% 初始化位置
particle(i).Position=CreateRandomSolution(model);

% 初始化速度
particle(i).Velocity=zeros(VarSize);

%评估
costP = CostFunction(particle(i).Position);
particle(i).Cost= costP;

% 更新个人最佳状态
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;

% 更新全球最佳
if particle(i).Best.Cost>GlobalBest.Cost
    GlobalBest=particle(i).Best;
end

end