∣ 旋转后仍为函数图像问题 Nightguard Series. ∣ \begin{vmatrix}\huge{\textsf{ 旋转后仍为函数图像问题 }}\\\texttt{ Nightguard Series. }\end{vmatrix} ∣∣∣∣∣ 旋转后仍为函数图像问题 Nightguard Series. ∣∣∣∣∣
♣ 例1 \clubsuit \textsf{例1} ♣例1
f ( x ) = ln ( x + 1 ) ( x ∈ ( 0 , + ∞ ) ) f(x)=\ln (x+1) (x\in(0,+\infin)) f(x)=ln(x+1)(x∈(0,+∞)) 的图像绕原点逆时针旋转 θ \theta θ 后仍为一个函数的图像,则 θ \theta θ 最大值为?
由函数的定义可知:一个
x
x
x 仅能对应一个
f
(
x
)
f(x)
f(x) ,或者说过图像上的任意一点
P
P
P 做与
x
x
x 轴垂直的直线,则该直线与图像仅有一个交点
P
P
P 。结合函数图像,我们可以找出一个临界位置:
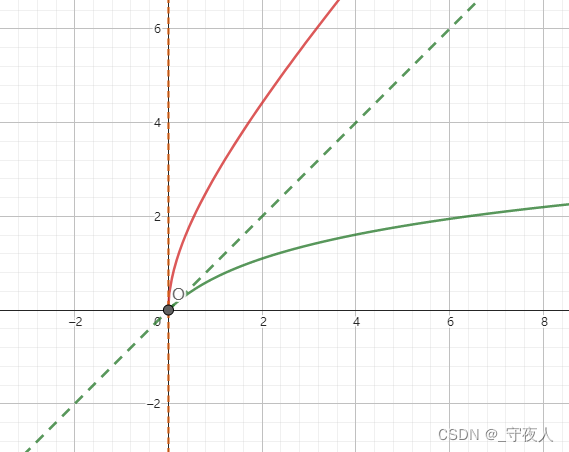
如图,当
f
(
x
)
=
ln
(
x
+
1
)
f(x)=\ln (x+1)
f(x)=ln(x+1) 的图像旋转的时候,其在
(
0
,
0
)
(0,0)
(0,0) 处的切线
l
l
l 也同时旋转。当
l
′
∥
y
l'\parallel y
l′∥y 轴时,即到达临界状态,如果继续旋转,则图像与
y
y
y 轴有两个交点,图像将不再是一个函数的图像。
而 f ′ ( x ) = 1 / ( x + 1 ) f'(x)=1/(x+1) f′(x)=1/(x+1) ,求得 l : y = x l:y=x l:y=x,倾斜角为 π 4 \frac{\pi}{4} 4π ,因此 θ \theta θ 最大值为 π 4 \frac{\pi}{4} 4π。
♣ 例2 \clubsuit \textsf{例2} ♣例2
f ( x ) = sin x ( x ∈ ( 0 , 2 π ) ) f(x)=\sin x (x\in(0,2\pi)) f(x)=sinx(x∈(0,2π)) 的图像绕原点顺时针旋转 θ \theta θ 后仍为一个函数的图像,则 θ \theta θ 最大值为?
与例1不同的是这题的临界状态与旋转中心处的切线无关:
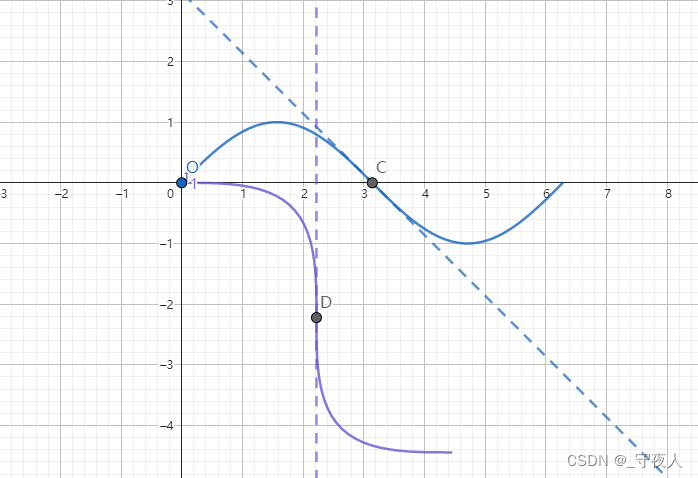
如图,当
f
(
x
)
=
sin
x
f(x)=\sin x
f(x)=sinx 的图像旋转的时候,其在
(
π
,
0
)
(\pi,0)
(π,0) 处的切线
l
l
l 也同时旋转。当
l
′
∥
y
l'\parallel y
l′∥y 轴时,即到达临界状态。
而 f ′ ( x ) = cos x f'(x)=\cos x f′(x)=cosx,求得 l : y = − x + π l:y=-x+\pi l:y=−x+π , θ \theta θ 最大值为 π 4 \frac{\pi}{4} 4π。
到此,我们发现一个规律:
顺时针旋转看 f ′ ( x ) m i n f'(x)_{min} f′(x)min, 逆时针旋转看 f ′ ( x ) m a x f'(x)_{max} f′(x)max
(应该是对的吧qaq)
♣ 例3 \clubsuit \textsf{例3} ♣例3
f ( x ) = ln ( x + 1 ) ( x ∈ ( 0 , + ∞ ) ) f(x)=\ln (x+1)(x\in(0,+\infin)) f(x)=ln(x+1)(x∈(0,+∞)) 的图像绕点 Q ( 114 , 514 ) Q(114,514) Q(114,514) 逆时针旋转 θ \theta θ 后仍为一个函数的图像,则 θ \theta θ 最大值为?
由于一个函数图像任意平移后一定还是一个函数图像,因此它与绕 ( 0 , 0 ) (0,0) (0,0) 点旋转的情况其实没有区别:
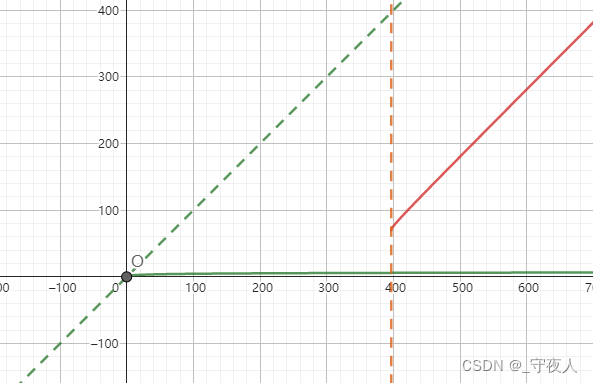
同时这也提示了例2的另一种思路:把原图像平移为
f
(
x
)
=
−
sin
x
(
x
∈
{
−
π
,
π
}
)
f(x)=-\sin x (x\in \{-\pi,\pi\})
f(x)=−sinx(x∈{−π,π}) ,可能会更好看一些。
♣ 例4 \clubsuit \textsf{例4} ♣例4(综合)
f ( x ) = x e x ( ( x ∈ ( 0 , + ∞ ) ) f(x)=\frac{x}{e^x} ((x\in(0,+\infin)) f(x)=exx((x∈(0,+∞)) 的图像绕原点逆时针旋转 θ \theta θ 后仍为一个函数的图像,则 θ \theta θ 取值范围是?
首先设 θ ∈ { − π , π } \theta \in\{-\pi,\pi\} θ∈{−π,π}
f ′ ( x ) = 1 − x e x f'(x)=\frac{1-x}{e^x} f′(x)=ex1−x
f ′ ′ ( x ) = x − 2 e x f''(x)=\frac{x-2}{e^x} f′′(x)=exx−2
x = 2 , f ′ ( x ) m i n = f ′ ( 2 ) = − 1 e 2 x=2,f'(x)_{min}=f'(2)=-\frac{1}{e^2} x=2,f′(x)min=f′(2)=−e21
∴ \therefore ∴ 逆时针方向上旋转最小角度为 − π 2 + arctan ( 1 e 2 ) -\frac{\pi}{2}+\arctan(\frac{1}{e^2}) −2π+arctan(e21)
x = 0 , f ′ ( x ) m a x = f ′ ( 0 ) = 1 x=0,f'(x)_{max}=f'(0)=1 x=0,f′(x)max=f′(0)=1
∴ \therefore ∴ 逆时针方向上旋转最大角度为 π 4 \frac{\pi}{4} 4π
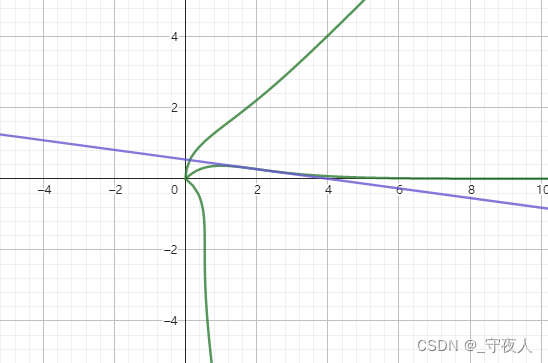
由周期性可知 θ ∈ [ k π − π 2 + arctan ( 1 e 2 ) , k π + π 4 ] , k ∈ Z . \theta \in[k\pi-\frac{\pi}{2}+\arctan(\frac{1}{e^2}),k\pi+\frac{\pi}{4}],k\in \Z. θ∈[kπ−2π+arctan(e21),kπ+4π],k∈Z.
![[附源码]计算机毕业设计JAVA学生考试成绩分析系统](https://img-blog.csdnimg.cn/3760c73c2deb4787ac40f1881b905df7.png)

![[附源码]Python计算机毕业设计Django基于VUE的网上订餐系统](https://img-blog.csdnimg.cn/6a15efb3e5be4b6bae628b111c2e33f4.png)