一：贪心算法

（1）概述

贪心算法概述：贪心算法可以认为是动态规划算法的一个特例，该算法需要满足的条件（贪心选择性质）要多余动态规划，但效率要比动态规划高。所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择（贪心选择）得到，当然这个问题只对部分问题成立

例如：你面前摆放着100张人民币，要求你只能拿十张，才能拿到最多的面额。显然，每次选择剩下钞票中面值最大的一张，最后选择一定是最优的
但现实中大部分问题不具有贪心选择性质，例如斗地主，对方出了“对3”，按照贪心策略，你应该尽可能出小的牌刚好压住对方，但现实情况并不这样，有可能我们会出王炸或其他牌。所以在这种情况下就只能使用动态规划解决了（这属于博弈问题）

（2）特点

贪心算法特点：

贪心算法法在解决问题的策略上“目光短浅”，只根据当前已有的求解信息就做出局部最优选择，而且一旦做出了选择，不管将来有什么结果，这个选择都不会改变
贪心法每次所做出的选择只是在某种意义上的局部最优选择，这种局部最优选择并不总能保证获得问题的整体最优解，但通常能获得近似最优解
在众多的计算机算法中，贪心策略是最接近人们日常思维的一种解题策略

（3）框架

框架：

Greedy(A, n) // A[1:n]代表n个输入
{
	Sort(A);
	solution = {}; //初始化解向量为空集
	for i to n do
		xi := Select(A)
		if Feasible(soltion, xi) then solution := Union(solution, xi)
		A = A - xi
		end if
		End for
		return (solution)
}

二：典型贪心算法问题

（1）无重叠区间

①：题目描述

给你很多形如 [start, end] 的闭区间，请你设计一个算法，算出这些区间中最多有几个互不相交的区间，注意边界相同不算相交

这个问题具有现实意义：比如你今天有好几个活动，每个活动都可以用区间 [start, end] 表示开始和结束的时间，请问你今天最多能参加几个活动呢？显然你一个人不能同时参加两个活动，所以说这个问题就是求这些时间区间的最大不相交子集

int intervalSchedule(int[][] intvs);

举个例子，intvs = [[1,3], [2,4], [3,6]]，这些区间最多有 2 个区间互不相交，即 [[1,3], [3,6]]，你的算法应该返回 2

②：解题思路

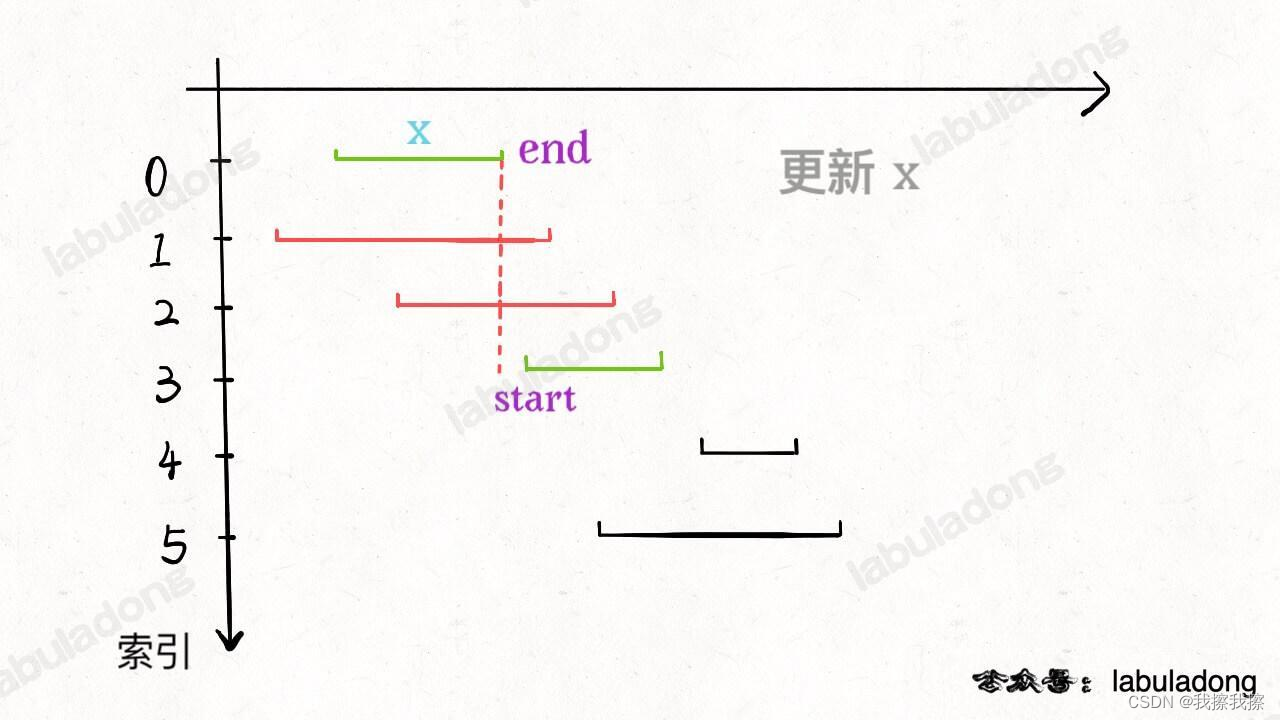
基本思路

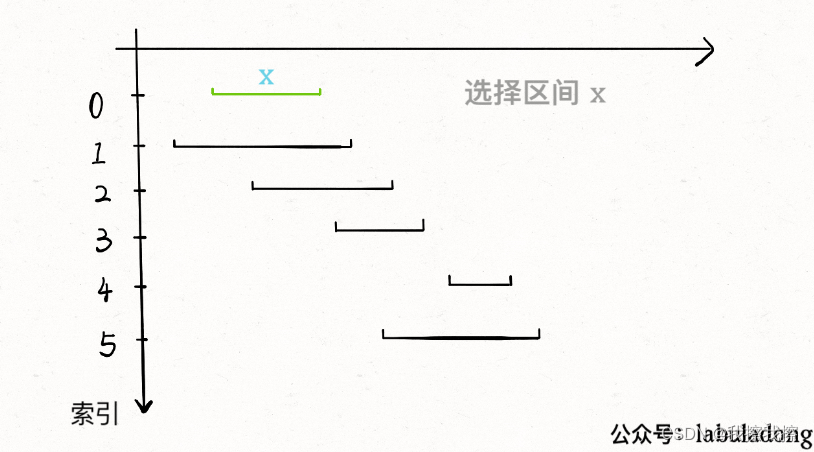
1：从区间集合intvs中选择一个区间 $x$ ，这个区间 $x$ 是在当前所有区间中结束最早的（也即end最小）
2：把所有与 $x$ 区间相交的区间从区间集合intvs中删除
3：重复步骤1和步骤2，知道intvs为空为止，此时所有选出的区间 $x$ 就是最大不想交子集

贪心算法在解决问题时往往首先需要对数据进行预处理（常见的就是排序），所以这里为了方便步骤1和步骤2，我们可以先按照每个区间的end进行排序，然后再去执行

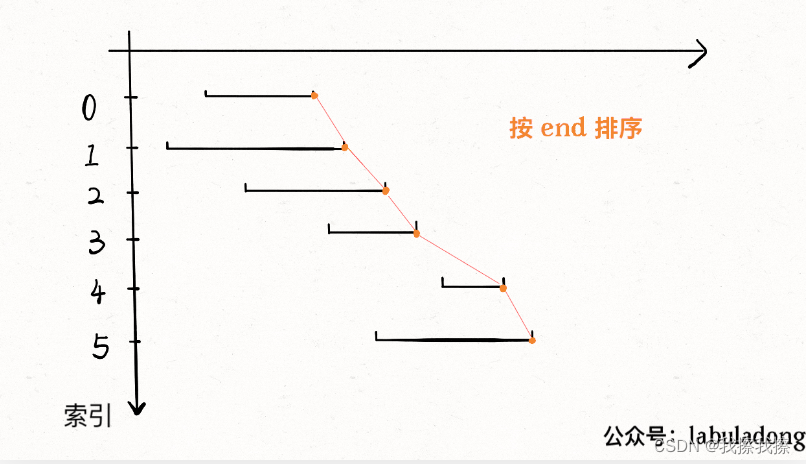
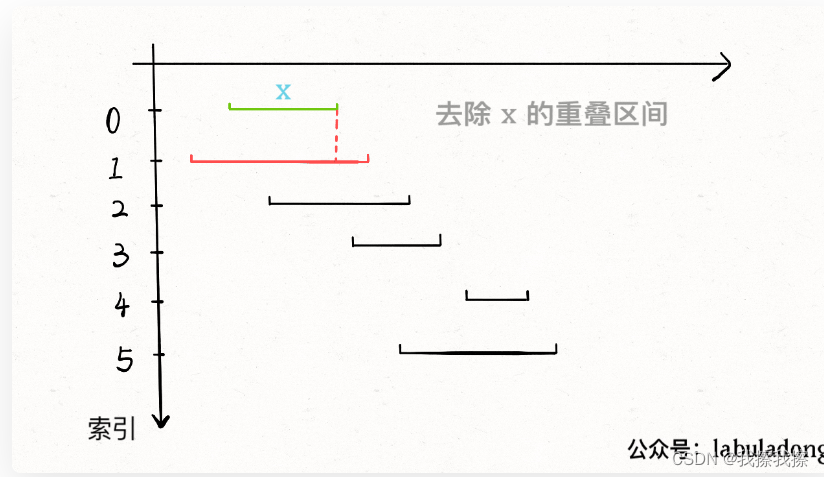
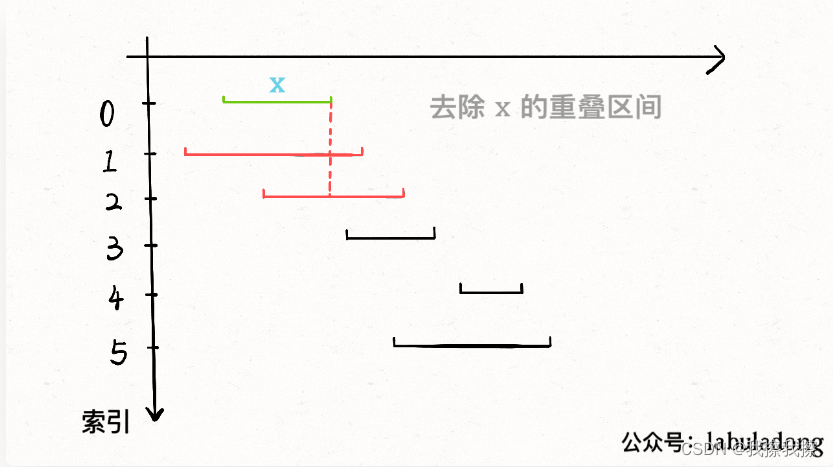
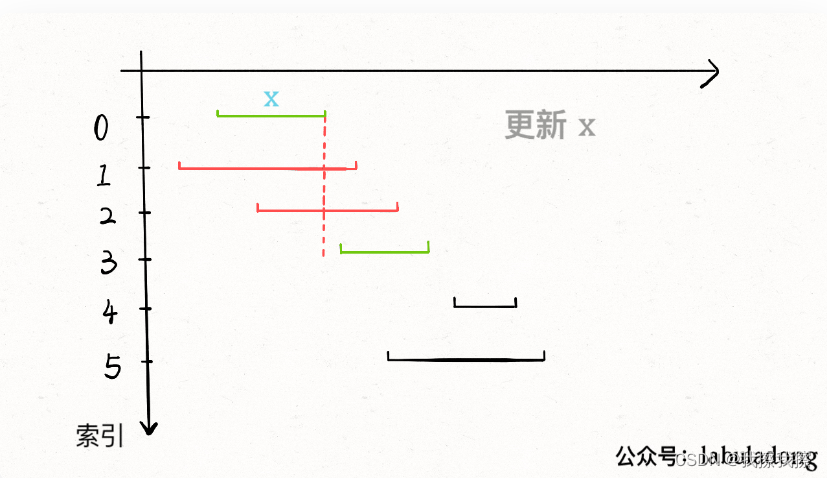
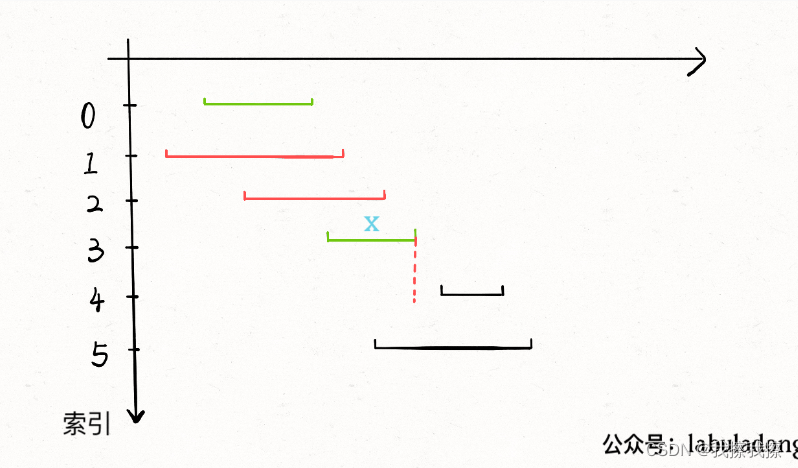
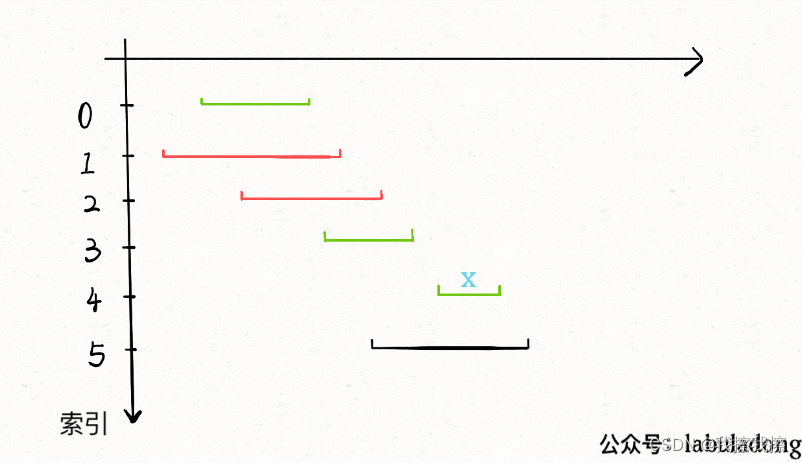
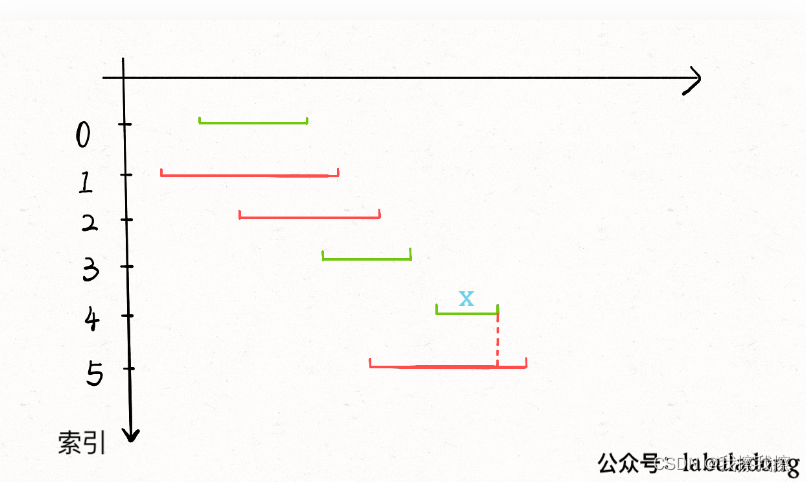
在这里插入图片描述

在判断是否相交时，如果它的start小于 $x$ 的end，那么就是相交的，防止则是不相交的

在这里插入图片描述

③：完整代码

这里采用Java，比较写反比较简单

class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        if(intervals.length == 0) return 0;
        //按照end进行升序排序
        Arrays.sort(intervals, new Comparator<int[]>(){
            public int compare(int[]a, int[]b){
                return a[1] - b[1];
            }
        });
        //count返回最大不相交区间，除非区间为空，所以至少有一个不相交的区间
        int count = 1;
        int x_end = intervals[0][1];
        for(int[] interval : intervals){
            int start = interval[0];
            if(start >= x_end){
                //说明终于找到了一个区间不相交
                count++;
                //更新下一个x
                x_end = interval[1];
            }
        }
        
        //注意题目问的是需要移除几个
        return intervals.length - count;
    }
}

（2）活动安排问题

①：题目描述

设有 $n$ 个活动的集合 $E = \{1,2,…,n\}$ ，其中每个活动都要求使用同一资源，如演讲会场等，而在同一时间内只有一个活动能使用这一资源。每个活动 $i$ 都有一个要求使用该资源的起始时间 $s_{i}$ 和一个结束时间 $f_{i}$ ，且 $s_{i} < f_{i}$ 。如果选择了活动 $i$ ，则它在半开时间区间 $s_{i}, f_{i})$ 内占用资源。若区间 $s_{i}, f_{i})$ 与区间 $s_{j}, f_{j})$ 不相交,则称活动 $i$ 与活动 $j$ 是相容的。也就是说，当 $s_{i}\geq f_{j}$ 或 $s_{j}\geq f_{i}$ 时，活动 $i$ 与活动 $j$ 相容。活动安排问题就是要在所给的活动集合中选出最大的相容活动子集合

②：解题思路

此问题本质就是无重叠区间问题，但相比上一题，我们需要把未重叠的子区间给打印出来

③：完整代码

class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        if(intervals.length == 0) return 0;
        // 用于保存最后的无重叠区间
        List<List<Integer>> arr = new ArrayList<>();

        //按照end进行升序排序
        Arrays.sort(intervals, new Comparator<int[]>(){
            public int compare(int[]a, int[]b){
                return a[1] - b[1];
            }
        });
        //count返回最大不相交区间，除非区间为空，所以至少有一个不相交的区间
        int count = 1;
        int x_end = intervals[0][1];

        List<Integer> first_temp = new ArrayList<>();
        first_temp.add(intervals[0][0]);
        first_temp.add(intervals[0][1]);
        arr.add(first_temp);

        for(int[] interval : intervals){
            
            int start = interval[0];
            if(start >= x_end){
                //说明终于找到了一个区间不相交
                List<Integer> temp = new ArrayList<>();
                temp.add(interval[0]);
                temp.add(interval[1]);
                arr.add(temp);

                count++;
                //更新下一个x
                x_end = interval[1];
            }
        }
        
        //注意题目问的是需要移除几个

        for(int i = 0; i < arr.size(); i++){
            System.out.println(arr.get(i));
        }
        return intervals.length - count;
    }
}