前言

本文旨在使用智能优化算法及其MATLAB实例（第2版） 一书中的例子，来透彻理解遗传算法的本质。

问题背景

目标：求解最大化函数 $\sin (5 x)+7 \cos (4 x)$ 的 $x$ ，其中 $x\in[0,10]$ 。

这个问题可以直接通过导数为0求解，但我们选择以此作为遗传算法的简单示例。

遗传算法的本质是优化后的穷搜算法， 事实上几乎所有此类启发式算法，本质都是用不同方式尽可能规避无效搜索后的优化版穷搜算法。

对于这个优化问题，变量 $x$ 为连续变量，可行解有无穷个，这样甚至连穷搜都不可行。因此，我们首先要将可行域离散化，使其可行解个数为有限个方能进行搜索。很简单的一种办法就是遗传算法中所谓的染色体编码：定义一个编码 $X$ 是一个 $L\times 1$ 的 $0 - 1$ 向量，例如：
$\cdots, 1]$
那么很显然，共有 $2^L$ 个不同的 $X$ 。我们可以认为每个 $X$ 都代表一个原问题中的可行 $x$ ，具体而言，我们可以定义函数：
$\frac{m\times 10} {2^L}, m = \sum_{i=1}^{L}2^{i-1}X_i$
那么 $g (X)$ 就代表了 $[0, 10]$ 之间的一个可行的 $x$ 。

通过均匀量化的方式，我们将无限的可行空间缩小成一个有限的可行空间。当 $L$ 足够大时，解的精度几乎不会受损。而这一简单的思想在遗传算法中就被称作听起来更高大上一些的染色体编码。

这样一来，使用穷搜算法的话，就是无脑遍历 $2^L$ 个解，选择最好的那个。接下来介绍遗传算法的搜索方式，以期在搜索数远少于 $2^L$ 次的情况下，搜到很好的解。

遗传算法

首先，获取初始种群，也就是先随机要搜索的 $N_P$ 个初始可行解 $X$ 。
对初始种群进行评估：计算这 $N_P$ 个解对应的目标函数大小。就本例而言，基于 $X$ 换算为 $x$ 后再计算 $f (x)$ 的值，记录对应最大 $f (x)$ 和最小 $f (x)$ 值的个体，也即 $X$ 。
计算适应度： 越优秀的个体，要有越大的概率遗传到下一代。我们以适应度来量化刻画优秀： $F=\frac{f(x)-f_{min}}{f_{max}-f_{min}}$
此处 $f_{min}$ 和 $f_{max}$ 代表了第二步中计算得到的当代种群的最优和最差解。经这一步操作，我们可以得到一个归一化的适应度结果 $F$ 。显然， $F\in[0,1]$ ，且是 $f (x)$ 的单调递增函数，也符合了我们优胜劣汰的遗传思想。
复制操作：从这一步开始我们准备基于初始种群生成下一代的种群了。首先，我们要基于适应度进行优胜劣汰： 更好的个体将有更大的概率进行复制，遗传到下一代种群。我们采用本例中所使用的所谓轮盘赌的选择准则：
$p_i=\frac{F_i}{\sum F_i}$
这里 $p_i$ 和 $F_i$ 分别代表第 $i$ 个个体被选中进行复制的概率和其对应的适应度。显然， $F_i$ 越大，被复制的概率越高。基于此，我们复制出下一代的 $N_p$ 个可行解 $X$ 。
(可以看到，表现最差的那个个体已不可能被复制，因为其 $F_i$ 为0。)
交叉操作：这个操作就是完全启发自遗传的思想了——父母结合产生新的下一代。具体而言， 将我们刚刚复制出来的下一代的 $N_p$ 个个体中，随机选择一对，将它们随机 $l$ 位的编码互换，从而更新这两个个体，创造出新的个体来。 在本例中，对复制好的 $N_p$ 个个体，我们按序两两成对，如1和2, 3和4，然后随机交换它们对应位的编码。每个位置交换与否的概率为 $0.5$ 。另外，对每一对选出的个体，都有20%的概率不进行交叉，有80%的概率执行刚刚所述的交叉。而80%则被称为交叉率。
变异操作： 除了通过交叉操作产生新个体，变异操作也是得到新个体的重要手段。 首先定义变异率 $p_m$ ，那么我们将随机选取 $p_m\times N_p$ 个个体进行变异。变异操作如下：对一个个体，随机挑选其 $L\times p_m$ 个基因（也即编码）进行变异，也即取反，从而得到一个新的个体。这里如果 $p_m\times L$ 的结果非整则还需取整。
保留最优：经过上述操作后，我们实际上已经生成了共有 $N_p$ 个个体的新一代种群。此时，我们将第一个个体踢掉，用上一代种群中最好的那个个体代替之。也即：下一代种群永远保留上一代的最优解。
判断是否已迭代到指定的遗传代数。如果没有，则跳转到第二步进行迭代。若已达到，选择最优的个体作为最终解。由于在每一代遗传时都保留了上一代的最优解，因此事实上我们的最终解就是所有搜索过的个体中的历史最优解。

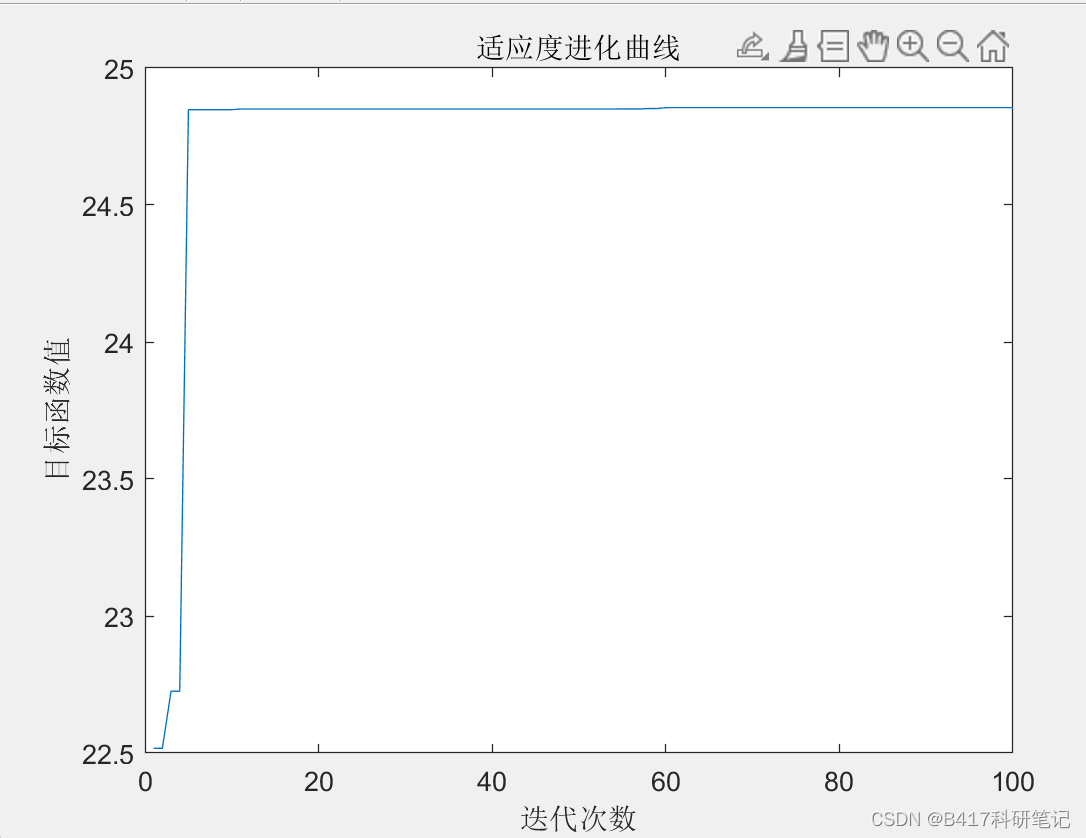
以上就是遗传算法的具体流程。 虽然看到许多文章会说他各种优点，但笔者看来，本质上就是如果基于一些启发式的（来自于自然的）思想进行更高效的搜索，虽然欠缺扎实的理论分析，但看上去就是个行之有效的方案。下面则是Matlab实例运行结果：

Matlab实例代码

在这里插入图片描述
作者给出的代码中用到了已被淘汰的randint API，这里笔者进行了修改使得可以直接在新版matlab上运行了，代码如下：

%%%%%%%%%%%%%%%%%%%%标准遗传算法求函数极值%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%初始化参数%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all;              %清除所有变量
close all;              %清图
clc;                    %清屏
NP=50;                  %种群数量
L=20;                   %二进制数串长度
Pc=0.8;                 %交叉率
Pm=0.1;                 %变异率
G=100;                  %最大遗传代数
Xs=10;                  %上限
Xx=0;                   %下限
f=randi(2, NP,L) - 1;        %随机获得初始种群
%%%%%%%%%%%%%%%%%%%%%%%%%遗传算法循环%%%%%%%%%%%%%%%%%%%%%%%%
for k=1:G
    %%%%%%%%%%%%将二进制解码为定义域范围内十进制%%%%%%%%%%%%%%
    for i=1:NP
        U=f(i,:);
        m=0;
        for j=1:L
            m=U(j)*2^(j-1)+m;
        end
        x(i)=Xx+m*(Xs-Xx)/(2^L-1);
        Fit(i)= func1(x(i));
    end
    maxFit=max(Fit);           %最大值
    minFit=min(Fit);           %最小值
    rr=find(Fit==maxFit);
    fBest=f(rr(1,1),:);        %历代最优个体   
    xBest=x(rr(1,1));
    Fit=(Fit-minFit)/(maxFit-minFit);  %归一化适应度值
    %%%%%%%%%%%%%%%%%%基于轮盘赌的复制操作%%%%%%%%%%%%%%%%%%%
    sum_Fit=sum(Fit);
    fitvalue=Fit./sum_Fit;
    fitvalue=cumsum(fitvalue);
    ms=sort(rand(NP,1));
    fiti=1;
    newi=1;
    while newi<=NP
        if (ms(newi))<fitvalue(fiti)
            nf(newi,:)=f(fiti,:);
            newi=newi+1;
        else
            fiti=fiti+1;
        end
    end   
    %%%%%%%%%%%%%%%%%%%%%%基于概率的交叉操作%%%%%%%%%%%%%%%%%%
    for i=1:2:NP
        p=rand;
        if p<Pc
            q=randi(2, 1,L) - 1;
            for j=1:L
                if q(j)==1
                    temp=nf(i+1,j);
                    nf(i+1,j)=nf(i,j);
                    nf(i,j)=temp;
                end
            end
        end
    end
    %%%%%%%%%%%%%%%%%%%基于概率的变异操作%%%%%%%%%%%%%%%%%%%%%%%
    i=1;
    while i<=round(NP*Pm)
        h=randi(NP);      %随机选取一个需要变异的染色体
        for j=1:round(L*Pm)         
            g=randi(L);   %随机需要变异的基因数
            nf(h,g)=~nf(h,g);
        end
        i=i+1;
    end
    f=nf;
    f(1,:)=fBest;                   %保留最优个体在新种群中
    trace(k)=maxFit;                %历代最优适应度
end
xBest;                              %最优个体
figure
plot(trace)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')

附录

君主方案

不同于轮盘赌方案，君主方案的交叉、变异、选择操作如下：

降序排列种群的个体适应度，选出适应度最高的个体作为“君主”。
将君主与其他偶数位的个体进行交叉，交叉的基因位个数决定于交叉率，例如交叉率为80%，基因位数10，则有8个基因将进行交叉置换。
基于变异率对所有个体进行变异，这一步操作与前例一致。至此得到 $N_p$ 个新个体。
将这 $N_p$ 个新个体与上一代的 $N_p$ 个老个体一并进行适应度评价，留下前 $N_p$ 个高适应度个体作为这一代的种群。、

遗传算法解决旅行商问题

假设有 $N$ 个城市，旅行商问题就是解决到这 $N$ 个城市的顺序问题，也即可行解 $X$ 为 $[1,2,\cdots, N]$ 的任意乱序排列。因此，我们可以将一个个体定义为一种乱序排列 (也即基因位数仍是 $32$ ，但取值不再是 $0, 1$ ，而是 $1,\cdots, N$ )，也即任意个体就是一个可行解。