前言

2022/11/12 我有幸参加了csdn第九次竞赛，终于拿了次满分，进了次前5，特写此题解

本次题目还是偏简单的，我不到$30min$就完成了$AK$，本以为第一稳到手，结果发现有三个比我快

接下来是题解

T1小艺读书

题意

书是人类进步的阶梯。 小艺每周因为工作的原因会选择性的每天多读几页或者少读几页。 小艺想知道一本n页的书她会在周几读完

分析

这是一道水题，由于n很小，直接模拟一遍就能过

#include<bits/stdc++.h>
using namespace std;
int d[10];
int main(){
	int n; cin >> n;
	for(int i=1;i<=7;i++)
		cin >> d[i];
	for(int i=1;;i++){
		if(i == 8) i = 1;
		n-= d[i];
		if(n <= 0){
			cout << i;
			break;
		}
	}
	return 0;
}

T2鬼画符门之宗门大比

题意

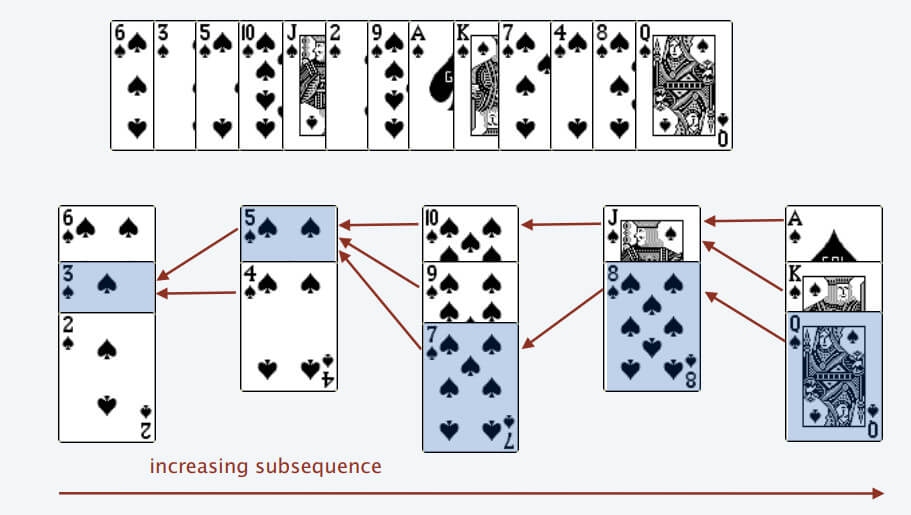
给定整数序列A。求在整数序列A中连续权值最大的子序列的权值。

分析

这是一道经典的题，有很多种方法，我用的是最快的方法-------贪心，
贪心策略如下：

• 用一个变量$ans$记录过程中的值，用$maxn$记录最大值
• 从$1$到$n$遍历整个序列，
  比如说遍历到第$i$个数，把$ans$加上$a_i$，并判断此时的$ans$是不是最大的，如果是，$maxn=ans$，即$maxn=\max (maxn,ans)$
  此时如果$ans<0$，那么选完这个数一定不是最优的，令$ans=0$
• 最后输出即可

代码

#include<bits/stdc++.h>
using namespace std;
int n;
int a[1100];
int main(){
	cin >> n;
	for(int i=1;i<=n;i++)
		cin >> a[i];
	int ans = 0 , maxn = -99999999;
	for(int i=1;i<=n;i++){
		ans += a[i];
		maxn = max(maxn,ans);
		if(ans < 0) ans = 0;
	}
	cout << maxn;
	return 0;
}

时间复杂度$O(n)$

别的方法

当然本题还有别的方法，这里介绍一下前缀和的方法
我们先预处理$a$数组的前缀和$sum$

for(int i=1;i<=n;i++)
	sum[i] = sum[i-1]+a[i];

那么对于序列中$l$到$r$区间的子串，这个区间的子串和为
$su{m}_r-su{m}_{l-1}$
那么我们可以枚举每一个子串，用前缀和$O(1)$算出这个子串和，更新最大值即可

for(int r=1;r<=n;r++)
	for(int l=1;l<=r;l++)
		maxn = max(maxn,sum[r]-sum[l-1]);

总时间复杂度$O(n^2)$，足以通过此题

当然因为$n\le 1000$(我记得好像是)，十分小，只要测评机够快，不用前缀和直接把每个子串和算出来也能过，时间复杂度$O(n^3)$，但实际上因为区间长短不同，实际时间远小于这个值，通过本题应该没问题，感兴趣的读者可以试试

T3硬币划分

题意

有1分，2分，5分，10分四种硬币，每种硬币数量无限，给定n分钱(n<=100000)，有多少中组合可以组成n分钱？

分析

n很大，答案也很大 (毕竟要对1e9+7取模)，显然是一道动态规划题

容易想到

状态

设$f_i$表示组成$i$分钱组合数

转移方程

显然，凑成$i$元钱，可以用

$i$ - $1$分钱 + $1$分钱
$i$ - $2$分钱 + $2$分钱
$i$ - $5$分钱 + $5$分钱
$i$ - $10$分钱 + $10$分钱

既然我们从小到大遍历，$i-1,i-2,i-5,i-10$的组合数显然是已知的，
那么
$$f_i=f_{i-1}+f_{i-2}+f_{i-5}+f_{i-10}$$
当然为了避免数组越界，我们可以这样写

for(int i=1;i<=n;i++)
	f[i] = (f[i]+f[i-1])%mod;
for(int i=2;i<=n;i++)
	f[i] = (f[i]+f[i-2])%mod;
for(int i=5;i<=n;i++)
	f[i] = (f[i]+f[i-5])%mod;
for(int i=10;i<=n;i++)
	f[i] = (f[i]+f[i-10])%mod;

当然也可以

for(int i=1;i<=n;i++){
	if(i>=1) f[i] = (f[i]+f[i-1])%mod;
	if(i>=2) f[i] = (f[i]+f[i-2])%mod;
	if(i>=5) f[i] = (f[i]+f[i-5])%mod;
	if(i>=10) f[i] = (f[i]+f[i-10])%mod;
}

不过写那么多$if$，常数较大，所以第一种方法更快 (虽然很小，差不了那零点零几秒)

初始值

$f_0=1$
或者也可以$f_1=f_2=f_5=f_{10}=1$，然后循环从$2,3,6,11$开始

代码

#include<bits/stdc++.h>
using namespace std;
const int mod = 1e9+7;
int n;
int f[110000];
int main(){
	cin >> n;
	f[0] = 1;
	for(int i=1;i<=n;i++)
		f[i] = (f[i]+f[i-1])%mod;
	for(int i=2;i<=n;i++)
		f[i] = (f[i]+f[i-2])%mod;
	for(int i=5;i<=n;i++)
		f[i] = (f[i]+f[i-5])%mod;
	for(int i=10;i<=n;i++)
		f[i] = (f[i]+f[i-10])%mod;
	cout << f[n];
	return 0;
}

T4饿龙咆哮-逃离城堡

题意

小艺酱误入龙族结界，被恶龙带回城堡，小艺酱决定逃离城堡，逃离龙族结界.。
总路程为c， 小艺酱的速度是vp，饿龙速度为vd。饿龙会在t小时后发现小艺酱出逃。
小艺酱担心自己跑不出去，准备了好多珍宝。 每当饿龙追上自己的时候小艺酱就会丢下一个珍宝，饿龙捡到珍宝会返回自
己的城堡进行研究，研究f小时后，再出城堡追赶小艺。
小艺想知道自己至少需要丢多少珍宝才能让自己安全逃出结界。

分析

这是一道很简单的数学题，小学我们就学过追及问题
$$t=路程差/速度差$$
我们只需算出会被追上几次，
每追上一次丢一次珍宝，然后计算饿龙回去并研究珍宝的时间，
然后再继续追

坑点

因为计算时时间不一定是整数，所以用$double$等小数类型储存，还有如果饿龙的速度比小艺酱的慢，直接特判输出$0$，不过我不知道官方数据中有没有这种数据

代码

#include<bits/stdc++.h>
using namespace std;
double vp,vd,t,f,c;
int main(){
	cin >> vp >> vd >> t >> f >> c;
	double s1 = vp*t , s2 = 0;
	int ans = 0;
	if(vp >= vd){//特判
		cout << 0;
		return 0;
	}
	while(s1 < c){
		t += (s1-s2)*1.0/(vd-vp);//计算追及时间
		s1 = s2 = t*vp;//现在路程
		if(s1 >= c) break;//一定要写前面，不然样例二过不去
		ans++;
		t += s2/vd+f;//饿龙回去研究后的时间
		s1 = vp*t;//现在路程
		s2 = 0;
	}
	cout << ans;
	return 0;
}

简化版

#include<bits/stdc++.h>
using namespace std;
double vp,vd,t,f,c;
int main(){
	cin >> vp >> vd >> t >> f >> c;
	double s = vp*t;
	int ans = 0;
	if(vp < vd)
		while(s < c){
			t += s*1.0/(vd-vp);
			s = t*vp;
			if(s >= c) break;
			ans++;
			t += s/vd+f;
		}
	cout << ans;
	return 0;
}

写在最后

本次竞赛难度不高，看最后有15个人满分
希望官方出题增加对数据结构和图论以及一些重要算法的考察