博主前期相关的博客可见下：
机器学习项目实战-能源利用率 Part-1（数据清洗）
机器学习项目实战-能源利用率 Part-2（探索性数据分析）
机器学习项目实战-能源利用率 Part-3（特征工程与特征筛选）
这部分进行的是：模型构建。

模型构建

导入预处理数据

import warnings
warnings.filterwarnings('ignore')

import pandas as pd
import numpy as np
pd.options.mode.chained_assignment = None
pd.set_option('display.max_columns', 50)

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.rcParams['font.size'] = 24
sns.set(font_scale = 2)

train_features = pd.read_csv('data/training_features.csv')
test_features = pd.read_csv('data/testing_features.csv')
train_labels = pd.read_csv('data/training_labels.csv')
test_labels = pd.read_csv('data/testing_labels.csv')
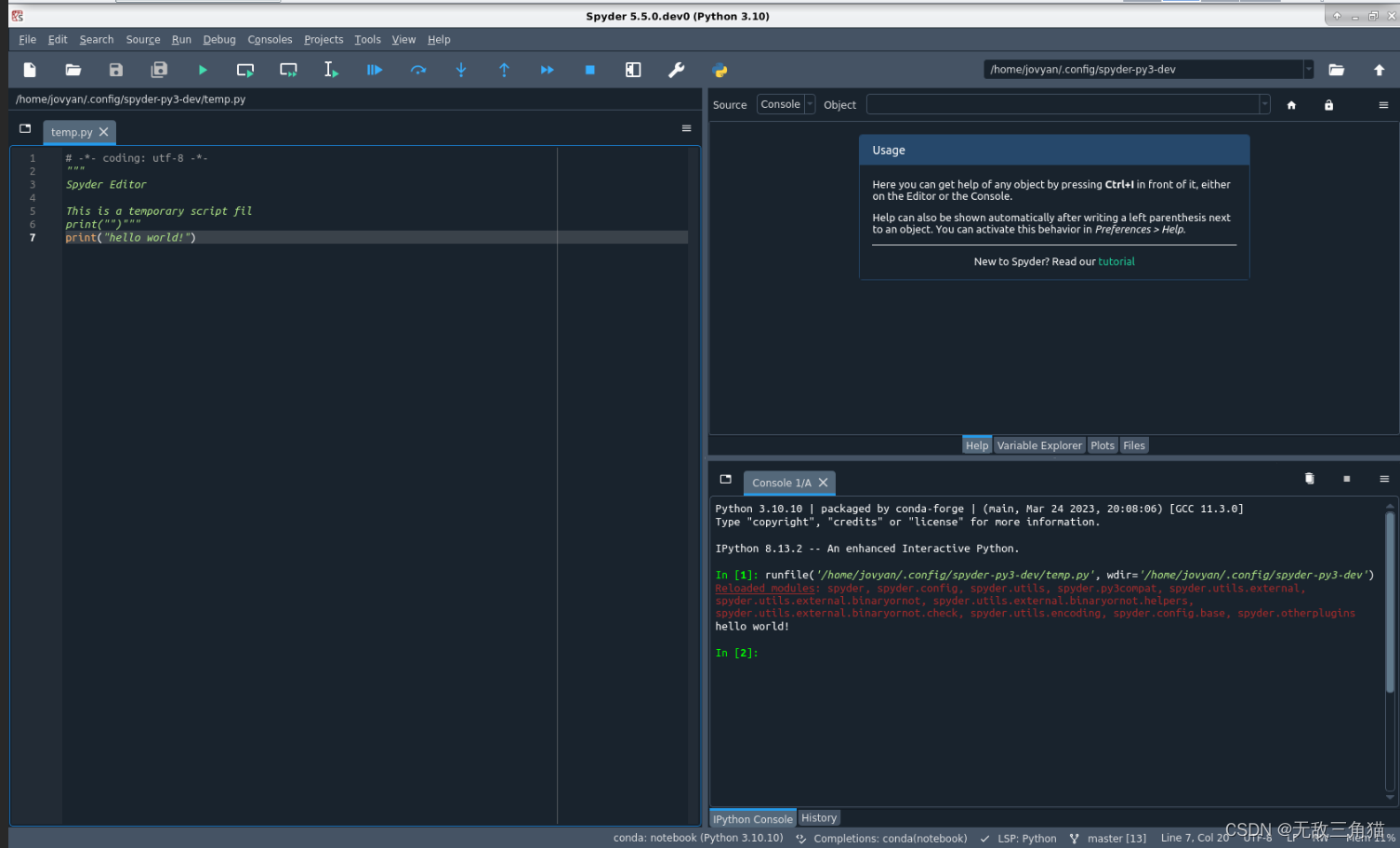
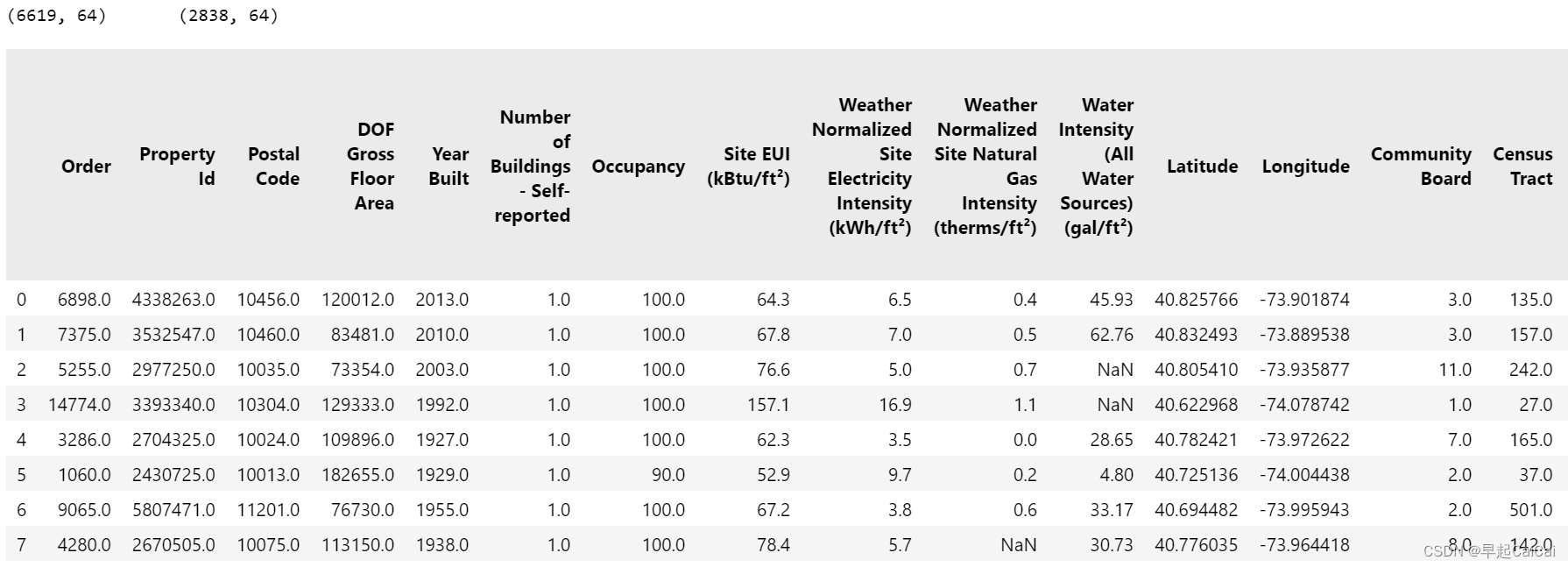
print(train_features.shape, '\t', test_features.shape)

train_features.head(8)

这段代码用于导入必要的Python库，读取训练和测试数据集，并显示训练集中的前8行数据。

• pd.options.mode.chained_assignment = None：设置pandas选项，以避免在链式赋值时显示警告信息。
• pd.set_option('display.max_columns', 50)：设置pandas选项，以显示所有列。
• sns.set(font_scale = 2)：设置seaborn的默认字体大小为2倍。

缺失值填充

在sklearn中，可以使用Scikit-learn Imputer object来进行缺失值填充，对于测试集我们使用数据集中的结果来进行填充，目的在于data leakage

from sklearn.impute import SimpleImputer

imputer = SimpleImputer(strategy = 'median')
imputer.fit(train_features)

X = imputer.transform(train_features)
X_test = imputer.transform(test_features)

print('Missing values in training features: ', np.sum(np.isnan(X)))
print('Missing values in testing features: ', np.sum(np.isnan(X_test)))

print(np.where(~np.isfinite(X)))
print(np.where(~np.isfinite(X_test)))

这段代码用于对特征数据集进行缺失值的处理。它使用了sklearn.impute模块中的SimpleImputer()函数来填补缺失值，并输出训练和测试特征数据集中的缺失值数量和位置。

• from sklearn.impute import SimpleImputer：从sklearn.impute模块导入SimpleImputer()函数，以填补缺失值。
• imputer = SimpleImputer(strategy = 'median')：创建一个SimpleImputer对象imputer，并指定使用median策略来填补缺失值。这意味着用中位数来代替缺失值。
• imputer.fit(train_features)：使用训练特征数据集来拟合imputer对象，以计算每个特征的中位数。
• X = imputer.transform(train_features)：使用transform()函数将训练特征数据集中的缺失值用中位数来代替，并将其存储在X中。
• X_test = imputer.transform(test_features)：使用transform()函数将测试特征数据集中的缺失值用中位数来代替，并将其存储在X_test中。
• print('Missing values in training features: ', np.sum(np.isnan(X)))：打印训练特征数据集中缺失值的数量，使用np.isnan()函数检查X中是否存在nan值，并使用np.sum()函数计算它们的数量。
• print('Missing values in testing features: ', np.sum(np.isnan(X_test)))：打印测试特征数据集中缺失值的数量，使用np.isnan()函数检查X_test中是否存在nan值，并使用np.sum()函数计算它们的数量。
• print(np.where(~np.isfinite(X)))：打印训练特征数据集中非有限数的位置，使用~np.isfinite()函数检查X中是否存在非有限数，并使用np.where()函数找到它们的位置。
• print(np.where(~np.isfinite(X_test)))：打印测试特征数据集中非有限数的位置，使用~np.isfinite()函数检查X_test中是否存在非有限数，并使用np.where()函数找到它们的位置补充说明一下，上述代码中的imputer对象使用中位数来填补缺失值是因为其在处理连续型特征时通常表现良好，而且对于离群值（outliers）也比较鲁棒。但是，在处理分类特征时，可能需要使用其他策略，例如众数（mode）或常数（constant）填充缺失值。在使用SimpleImputer函数时，还可以通过指定strategy参数来选择不同的填充策略。

特征归一化

from sklearn.preprocessing import MinMaxScaler  # StandardScaler
minmax_scaler = MinMaxScaler()
minmax_scaler.fit(X)
X = minmax_scaler.transform(X)
X_test = minmax_scaler.transform(X_test)

y = np.array(train_labels).reshape((-1, ))
y_test = np.array(test_labels).reshape((-1, ))

这段代码用于对填补缺失值后的特征数据集进行缩放处理，以及将标签数据集转换为numpy数组。

• from sklearn.preprocessing import MinMaxScaler：从sklearn.preprocessing模块导入MinMaxScaler()函数，用于对数据进行归一化缩放处理。
• minmax_scaler = MinMaxScaler()：创建一个MinMaxScaler对象minmax_scaler。
• minmax_scaler.fit(X)：使用训练特征数据集X来拟合minmax_scaler对象，以计算每个特征的最大值和最小值。
• X = minmax_scaler.transform(X)：使用transform()函数将训练特征数据集进行缩放处理，并将其存储在X中。
• X_test = minmax_scaler.transform(X_test)：使用transform()函数将测试特征数据集进行缩放处理，并将其存储在X_test中。
• y = np.array(train_labels).reshape((-1, ))：将训练标签数据集train_labels转换为numpy数组，并使用reshape()函数将其转换为一维数组（即行向量），并将其存储在y中。
• y_test = np.array(test_labels).reshape((-1, ))：将测试标签数据集test_labels转换为numpy数组，并使用reshape()函数将其转换为一维数组（即行向量），并将其存储在y_test中。

这段代码中使用的是MinMaxScaler()函数进行缩放处理，它将每个特征缩放到给定的范围（默认为[0, 1]）。这种缩放方法对于许多机器学习算法来说是非常有用的，因为它可以将不同特征的值域缩放到相同的范围内，避免了某些特征对模型产生过大的影响。如果需要进行标准化处理，可以使用StandardScaler()函数，它将每个特征缩放到均值为0，方差为1的标准正态分布中。

建立一个baseline

在建模之前，我们得有一个最坏的打算，就是模型起码得有点作用才行。

def mae(y_true, y_pred):
	return np.mean(abs(y_true - y_pred))
baseline_guess = np.median(y)

print('The baseline guess is a score of %.2f' % baseline_guess)
print('Baseline Performance on the test set: MAE = %.4f' % mae*y_test, baseline_guess))

这段代码定义了一个计算平均绝对误差（MAE）的函数mae()，并使用中位数来计算基准猜测的得分。然后，它打印出基准猜测值和在测试集上计算的基准性能的MAE。

• def mae(y_true, y_pred):：定义了一个名为mae的函数，它有两个参数y_true和y_pred，分别表示真实标签和预测标签。
• return np.mean(abs(y_true - y_pred))：函数的主体是返回真实标签和预测标签之间的平均绝对误差（MAE）。
• baseline_guess = np.median(y)：使用numpy中的median()函数计算训练标签数据集y的中位数，并将其存储在baseline_guess中。这个中位数值将被用作基准猜测的得分。
• print('The baseline guess is a score of %.2f' % baseline_guess)：打印基准猜测的得分，使用%占位符来将baseline_guess插入到输出字符串中，并使用%.2f来指定浮点数输出的格式为两个小数点。
• print('Baseline Performance on the test set: MAE = %.4f' % mae*y_test, baseline_guess))：打印基准性能的MAE，使用%占位符来将mae*y_test和baseline_guess插入到输出字符串中，并使用%.4f来指定浮点数输出的格式为四个小数点。mae*y_test表示使用mae()函数计算真实标签和基准猜测之间的平均绝对误差，并乘以测试标签数据集y_test的长度，以得到总误差。最后，它将baseline_guess作为第二个参数传递给mae()函数，作为预测标签的值，因为基准猜测的预测标签是一个常数。
  

选择的机器学习算法（回归问题）

• Linear Regression
• Logistic Regression
• Support Vector Machine Regression
• Random Forest Regression
• Decision Tree Regressor
• Gradient Boosting Regression
• SGDRegressor
• K-Nearest Neighbors Regression

def mae(y_true, y_pred):
	return np.mean(abs(y_true - y_pred))
def fit_and_evaluate(mode):
	model.fit(X, y)
	model_pred = model.predict(X_test)
	model_mae = mae(y_test, model_pred)
	return model_mae

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr_mae = fit_and_evaluate(lr)
print('Linear Regression Performance on the test set: MAE = %.4f' % lr_mae)

from sklearn.linear_model import LogisticRegression
logistic = LogisticRegression()
logistic_mae = fit_and_evaluate(logistic)
print('Logistic Regression Performance on the test set: MAE = %.4f' % logistic_mae)

from sklearn.svm import SVR
svm = SVR(C = 1000, gamma = 0.1)
svm_mae = fit_and_evaluate(svm)
print('Support Vector Machine Regression Performance on the test set: MAE = %.4f' % svm_mae)

from sklearn.ensemble import RandomForestRegressor
rfr = RandomForestRegressor(random_state = 42)
rfr_mae = fit_and_evaluate(rfr)
print('Random Forest Regressor Performance on the test set: MAE = %.4f' % rfr_mae)

from sklearn.tree import DecisionTreeRegressor
dtr = DecisionTreeRegressor()
dtr_mae = fit_and_evaluate(dtr)
print('Decision Tree Regressor Performance on the test set: MAE = %.4f' % dtr_mae)

from sklearn.ensemble import GradientBoostingRegressor
gbr = GradientBoostingRegressor()
gbr_mae = fit_and_evaluate(gbr)
print('Gradient Boosting Regressor Performance on the test set: MAE = %.4f' % gbr_mae)

from sklearn.linear_model import SGDRegressor
sgdr = SGDRegressor(random_state = 42)
sgdr_mae = fit_and_evaluate(sgdr)
print('SGDRegressor Performance on the test set: MAE = %.4f' % sgdr_mae)

from sklearn.neighbors import KNeighborsRegressor
knn = KNeighorsRegressor(n_neighbors = 10)
knn_mae = fit_and_evaluate(knn)
print('K-Nearest Neighbors Regressor Performance on the test set: MAE = %.4f' % knn_mae)

plt.style.use('fivethirtyeight')
plt.figure(figsize = (12, 8))

model_comparison = pd.DataFrame({'model': ['Linear Regression', 'Logistic Regression',
                                           'Support Vector Machine', 'Random Forest',
                                           'Decision Tree', 'Gradient Boosting',
                                           'SGDRegressor', 'K-Nearest Neighbors'],
                                'mae': [lr_mae, logistic_mae, svm_mae, rfr_mae,
                                       dtr_mae, gbr_mae, sgdr_mae, knn_mae]})
model_comparison.sort_values('mae',ascending=False).plot(x='model',y='mae',kind='barh',
                                                        color='red', edgecolor='black')
plt.ylabel(''); plt.xlabel('Mean Absolute Error')
plt.yticks(size = 14); plt.xticks(size = 14)
plt.title('Model Comparison on Test MAE', size = 20);

这段代码用于绘制不同模型在测试集上的平均绝对误差（MAE）比较图。

• plt.style.use('fivethirtyeight')：设置matplotlib的样式，使用fivethirtyeight风格。
• plt.figure(figsize = (12, 8))：创建一个新的figure对象，并设置其大小为(12, 8)。
• model_comparison = pd.DataFrame({'model': ['Linear Regression', 'Logistic Regression', 'Support Vector Machine', 'Random Forest','Decision Tree', 'Gradient Boosting','SGDRegressor', 'K-Nearest Neighbors'],'mae': [lr_mae, logistic_mae, svm_mae, rfr_mae,dtr_mae, gbr_mae, sgdr_mae, knn_mae]})：创建一个名为model_comparison的DataFrame对象，其中包含每个模型的名称和在测试集上计算的MAE值。
• model_comparison.sort_values('mae',ascending=False).plot(x='model',y='mae',kind='barh',color='red', edgecolor='black')：对model_comparison数据按照MAE值进行排序，并绘制水平条形图，其中x轴为模型名称，y轴为MAE值。kind='barh'表示绘制水平条形图，color='red'表示设置条形图的颜色为红色，edgecolor='black'表示设置条形图的边框颜色为黑色。

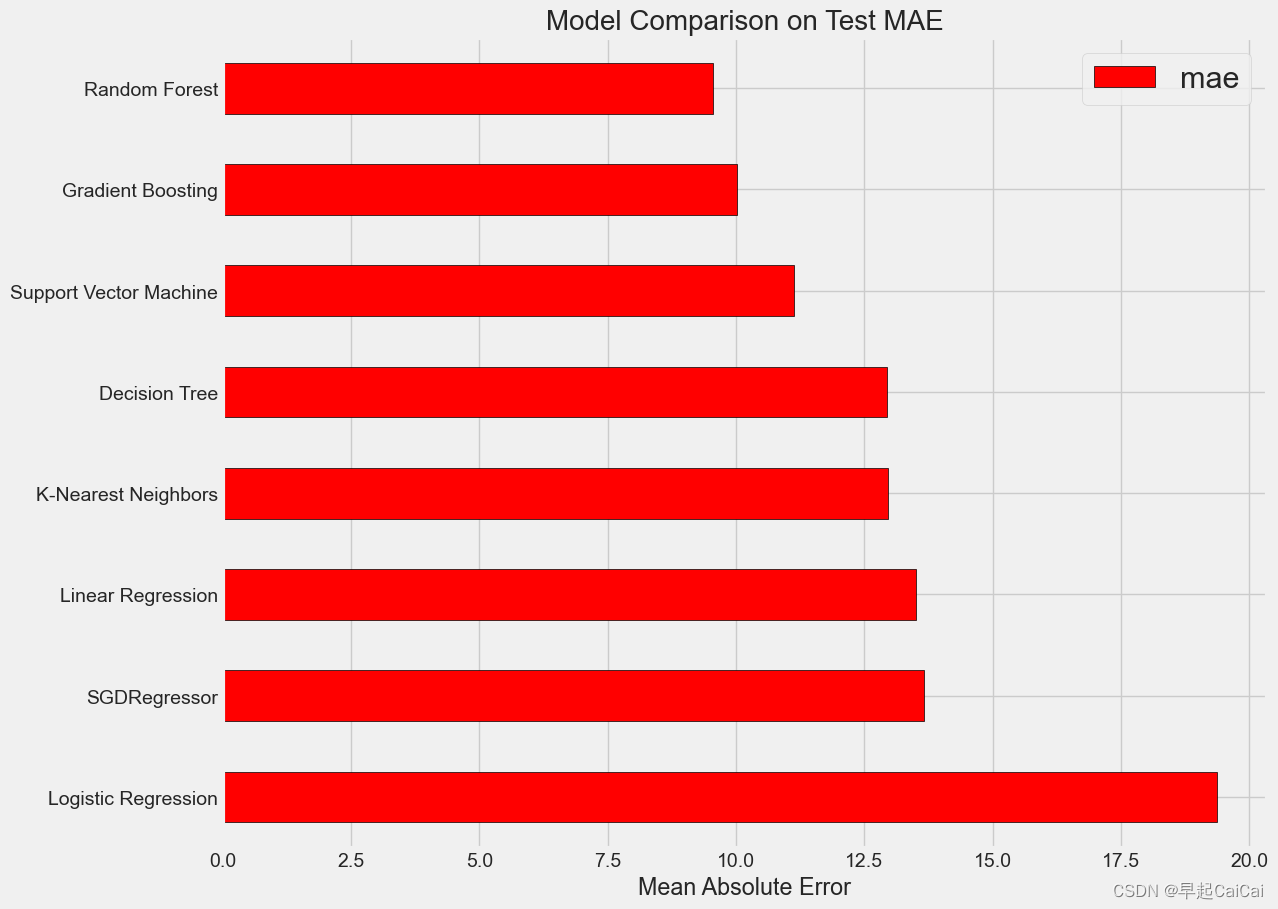
看起来随机森林和集成算法比较占优势一些，这里存在一些不公平，因为参数只用了默认，但是对于SVM来说参数可能影响会更大一些。

模型调参

5.1 RandomizedSearchCV

from sklearn.model_selection import RandomizedSearchCV

loss = ['ls', 'lad', 'huber']
n_estimators = [100, 500, 1000, 1500]
max_depth = [2, 3, 5, 10]
min_samples_leaf = [1, 2, 4, 6, 8]
min_samples_split = [2, 4, 6, 10]
max_features = ['auto', 'sqrt', 'log2', None]

hyperparameter_grid = {'loss':loss, 'min_samples_split':min_samples_split,
                       'max_depth':max_depth,'min_samples_leaf':min_samples_leaf,
                       'n_estimators':n_estimators,'max_features':max_features}
model = GradientBoostingRegressor(random_state = 42)
random_cv = RandomizedSearchCV(estimator = model, cv = 3, n_iter = 30, verbose = 1,
                              param_distributions = hyperparameter_grid,
                              scoring = 'neg_mean_absolute_error', n_jobs = -1,
                              return_train_score = True, random_state = 42)
random_cv.fit(X, y)

random_cv.best_estimator_

这段代码用于使用随机搜索来调整梯度提升回归模型的超参数，并输出最佳模型的参数设置。

• from sklearn.model_selection import RandomizedSearchCV：从sklearn.model_selection模块导入RandomizedSearchCV函数，用于使用随机搜索来调整模型参数。
• loss = ['ls', 'lad', 'huber']：创建一个名为loss的列表，包含三种不同的损失函数类型。
• n_estimators = [100, 500, 1000, 1500]：创建一个名为n_estimators的列表，包含不同的弱学习器的数量。
• max_depth = [2, 3, 5, 10]：创建一个名为max_depth的列表，包含不同的最大树深度。
• min_samples_leaf = [1, 2, 4, 6, 8]：创建一个名为min_samples_leaf的列表，包含不同的叶节点最小样本数。
• min_samples_split = [2, 4, 6, 10]：创建一个名为min_samples_split的列表，包含不同的内部节点最小样本数。
• max_features = ['auto', 'sqrt', 'log2', None]：创建一个名为max_features的列表，包含不同的最大特征数量。
• hyperparameter_grid = {'loss':loss, 'min_samples_split':min_samples_split, 'max_depth':max_depth,'min_samples_leaf':min_samples_leaf,'n_estimators':n_estimators,'max_features':max_features}：创建一个名为hyperparameter_grid的字典，包含前面定义的不同超参数值的所有组合。
• model = GradientBoostingRegressor(random_state = 42)：创建一个GradientBoostingRegressor对象model，并将随机数生成器的种子设置为42。
• random_cv = RandomizedSearchCV(estimator = model, cv = 3, n_iter = 30, verbose = 1, param_distributions = hyperparameter_grid, scoring = 'neg_mean_absolute_error', n_jobs = -1, return_train_score = True, random_state = 42)：创建一个RandomizedSearchCV对象random_cv，用于对model对象进行随机搜索。cv=3表示使用3折交叉验证，n_iter=30表示进行30次不同参数组合的随机搜索，verbose=1表示打印详细信息，param_distributions=hyperparameter_grid表示搜索的参数组合使用前面定义的hyperparameter_grid字典，scoring='neg_mean_absolute_error'表示使用平均绝对误差（MAE）作为度量模型性能的指标，n_jobs=-1表示使用所有可用的CPU内核来运行搜索，return_train_score=True表示返回训练集上的性能指标，random_state=42表示设置随机数生成器的种子为42。
• random_cv.fit(X, y)：使用训练特征数据集X和训练标签数据集y来拟合random_cv对象，进行随机搜索优化模型的超参数。
• random_cv.best_estimator_：输出最佳模型的参数设置，包括损失函数类型、内部节点最小样本数、最大树深度、叶节点最小样本数、弱学习器数量、最大特征数量等。

random_cv.best_estimator_.fit(X, y)
random_cv_pred = random_cv.best_estimator_.predict(X_test)
mae(y_test, random_cv_pred)

最佳参数的结果是9.1255；未调参之前是9.5588

GridSearchCV

from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import GradientBoostingRegressor

trees_grid = {'min_samples_split': [6, 10], 'min_samples_leaf': [4, 6],
              'max_depth': [5, 6], 'loss': ['huber', 'lad']}

model = GradientBoostingRegressor(max_features=None, n_estimators=500, random_state=42)

grid_search = GridSearchCV(estimator=model, param_grid=trees_grid, cv=3, verbose=1,
                          scoring='neg_mean_absolute_error', n_jobs=-1, return_train_score=True)

grid_search.fit(X, y)

print(grid_search.best_estimator_)

这段代码用于使用网格搜索来调整梯度提升回归模型的超参数，并输出最佳模型的参数设置。

• from sklearn.model_selection import GridSearchCV：从sklearn.model_selection模块导入GridSearchCV函数，用于使用网格搜索来调整模型参数。
• from sklearn.ensemble import GradientBoostingRegressor：从sklearn.ensemble模块导入GradientBoostingRegressor类，用于创建梯度提升回归模型。
• trees_grid = {'min_samples_split': [6, 10], 'min_samples_leaf': [4, 6], 'max_depth': [5, 6], 'loss': ['huber', 'lad']}：创建一个名为trees_grid的字典，包含要搜索的超参数及其取值范围。
• model = GradientBoostingRegressor(max_features=None, n_estimators=500, random_state=42)：创建一个GradientBoostingRegressor对象model，并将最大特征数量设置为None，弱学习器数量设置为500，随机数种子设置为42。
• grid_search = GridSearchCV(estimator=model, param_grid=trees_grid, cv=3, verbose=1, scoring='neg_mean_absolute_error', n_jobs=-1, return_train_score=True)：创建一个GridSearchCV对象grid_search，用于对model对象进行网格搜索。estimator=model表示要优化的模型为model对象，param_grid=trees_grid表示搜索的参数组合使用前面定义的trees_grid字典，cv=3表示使用3折交叉验证，verbose=1表示打印详细信息，scoring='neg_mean_absolute_error'表示使用平均绝对误差（MAE）作为度量模型性能的指标，n_jobs=-1表示使用所有可用的CPU内核来运行搜索，return_train_score=True表示返回训练集上的性能指标。
• grid_search.fit(X, y)：使用训练特征数据集X和训练标签数据集y来拟合grid_search对象，进行网格搜索优化模型的超参数。
• print(grid_search.best_estimator_)：输出最佳模型的参数设置，包括内部节点最小样本数、叶节点最小样本数、最大树深度、损失函数类型等。
  

再来一次, 单独搜索n_estimators

trees_grid = {'n_estimators': [100, 150, 200, 250, 300, 350, 400, 450, 500, 550, 600, 650, 700, 750, 800]}

model = GradientBoostingRegressor(loss='lad', max_features=None, max_depth=6,
                                 min_samples_leaf=4, min_samples_split=10, random_state=42)

grid_search = GridSearchCV(estimator=model, param_grid=trees_grid, cv=3, verbose=1,
                          scoring='neg_mean_absolute_error', n_jobs=-1, return_train_score=True)

grid_search.fit(X, y)

results = pd.DataFrame(grid_search.cv_results_)

plt.figure(figsize=(8, 8))
plt.plot(results['param_n_estimators'], -1*results['mean_test_score'], label='Testing Error')
plt.plot(results['param_n_estimators'], -1*results['mean_train_score'], label='Training Error')
plt.xlabel('Number of Trees'); plt.ylabel('Mean Absolute Error')
plt.title('Performance vs Number of Trees')
plt.legend()

这段代码用于单独搜索梯度提升回归模型的弱学习器数量（即n_estimators），并绘制在不同弱学习器数量下的训练误差和测试误差的变化曲线。

• trees_grid = {'n_estimators': [100, 150, 200, 250, 300, 350, 400, 450, 500, 550, 600, 650, 700, 750, 800]}：创建一个名为trees_grid的字典，包含要搜索的超参数n_estimators及其取值范围。
• model = GradientBoostingRegressor(loss='lad', max_features=None, max_depth=6, min_samples_leaf=4, min_samples_split=10, random_state=42)：创建一个GradientBoostingRegressor对象model，并将损失函数类型设置为lad，最大特征数量设置为None，最大树深度设置为6，叶节点最小样本数设置为4，内部节点最小样本数设置为10，随机数生成器的种子设置为42。
• grid_search = GridSearchCV(estimator=model, param_grid=trees_grid, cv=3, verbose=1, scoring='neg_mean_absolute_error', n_jobs=-1, return_train_score=True)：创建一个GridSearchCV对象grid_search，用于对model对象进行网格搜索。estimator=model表示要优化的模型为model对象，param_grid=trees_grid表示搜索的参数组合使用前面定义的trees_grid字典，cv=3表示使用3折交叉验证，verbose=1表示打印详细信息，scoring='neg_mean_absolute_error'表示使用平均绝对误差（MAE）作为度量模型性能的指标，n_jobs=-1表示使用所有可用的CPU内核来运行搜索，return_train_score=True表示返回训练集上的性能指标。
• grid_search.fit(X, y)：使用训练特征数据集X和训练标签数据集y来拟合grid_search对象，进行网格搜索优化模型的超参数。
• results = pd.DataFrame(grid_search.cv_results_)：将网格搜索结果存储在一个名为results的DataFrame对象中。
• plt.figure(figsize=(8, 8))：设置绘制图形的大小。
• plt.plot(results['param_n_estimators'], -1*results['mean_test_score'], label='Testing Error')：绘制测试误差的变化曲线，横坐标为弱学习器数量（即n_estimators），纵坐标为平均绝对误差的相反数。-1*results['mean_test_score']表示相反数，label='Testing Error'表示添加图例标签。

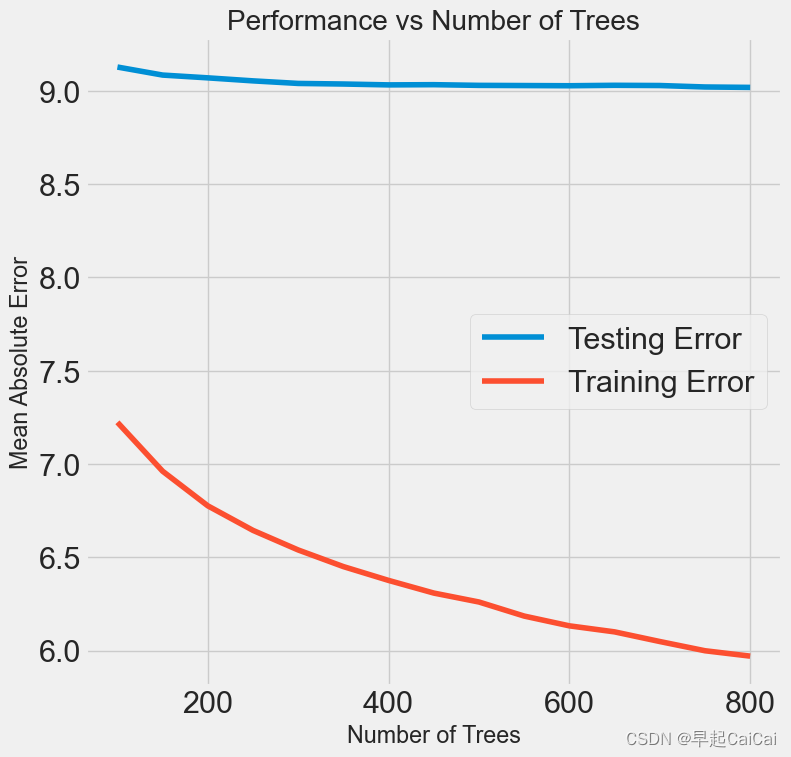
上图有训练的误差，测试的误差

results.sort_values('mean_test_score', ascending = False).head()

这段代码用于在网格搜索的结果中，按照测试误差（平均绝对误差）从大到小排序，输出测试误差最大的前五个模型的参数设置和性能指标。

• results.sort_values('mean_test_score', ascending = False)：对results对象按照测试误差的平均值进行降序排序，即从大到小排序。'mean_test_score'表示按照测试误差的平均值进行排序，ascending=False表示降序排列。
• .head()：仅显示前五个结果，即测试误差最大的前五个模型的参数设置和性能指标。

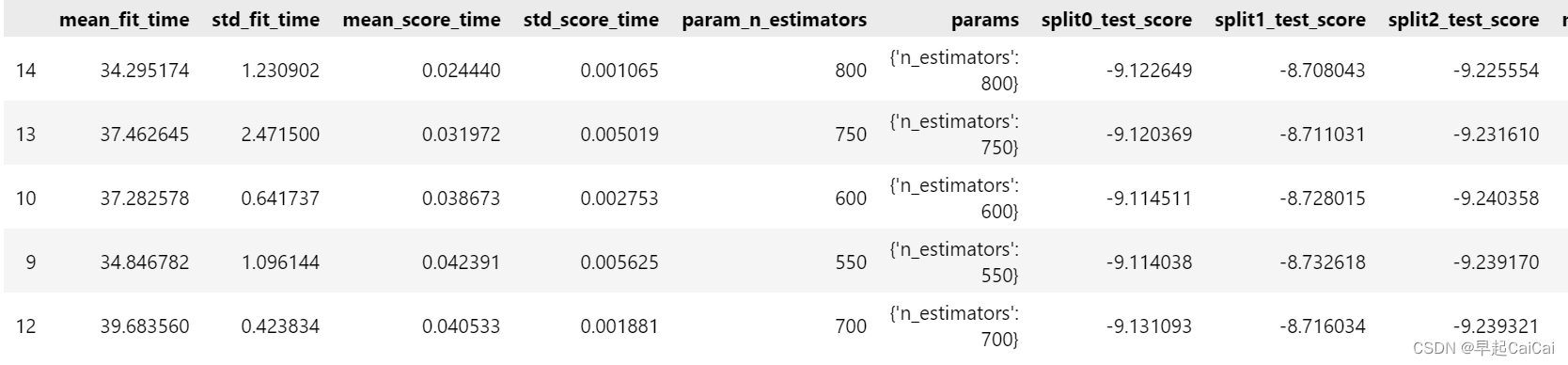
测试模型

default_model = GradientBoostingRegressor(random_state = 42)
final_model = grid_search.best_estimator_
final_model

%%timeit -n 1 -r 5
default_model.fit(X, y)

这段代码使用Jupyter Notebook的%%timeit魔术命令来测试模型拟合所需的时间（单位为秒）。

• %%timeit：使用Jupyter Notebook的%%timeit魔术命令来测试代码执行的时间。
• -n 1：表示执行一次测试。
• -r 5：表示执行5轮测试，每轮测试输出一个平均值和一个标准差。
• default_model.fit(X, y)：使用default_model对象对训练数据集X和标签数据集y进行拟合，即训练模型。default_model对象是使用默认参数设置创建的梯度提升回归模型。fit方法返回的是拟合后的模型对象，但在此处并未使用。

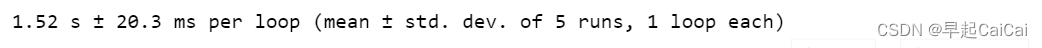
default_model

%%timeit -n 1 -r 5
final_model.fit(X, y)

final_model

default_pred = default_model.predict(X_test)
final_pred = final_model.predict(X_test)

print('Default model performance on the test set:MAE = %.4f.' % mae(y_test, default_pred))
print('Final model performance on the test set:  MAE = %.4f.' % mae(y_test, final_pred))

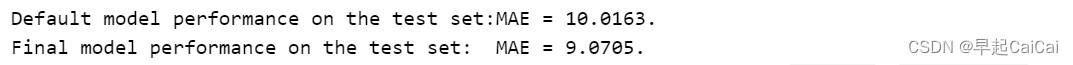
plt.figure(figsize = (8, 8))

sns.kdeplot(default_pred, label = 'Default Predictions')
sns.kdeplot(final_pred, label = 'Predictions')
sns.kdeplot(y_test, label = 'Values')
plt.xlabel('Energy Star Score'); plt.ylabel('Density')
plt.title('Test Values and Predictions')

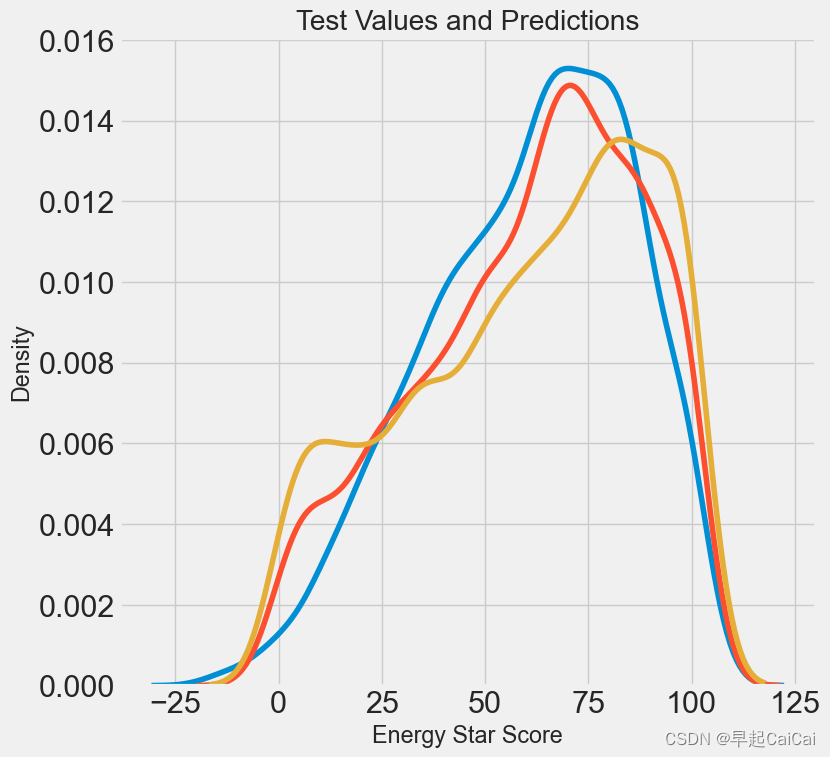
比较优化的模型与默认的模型

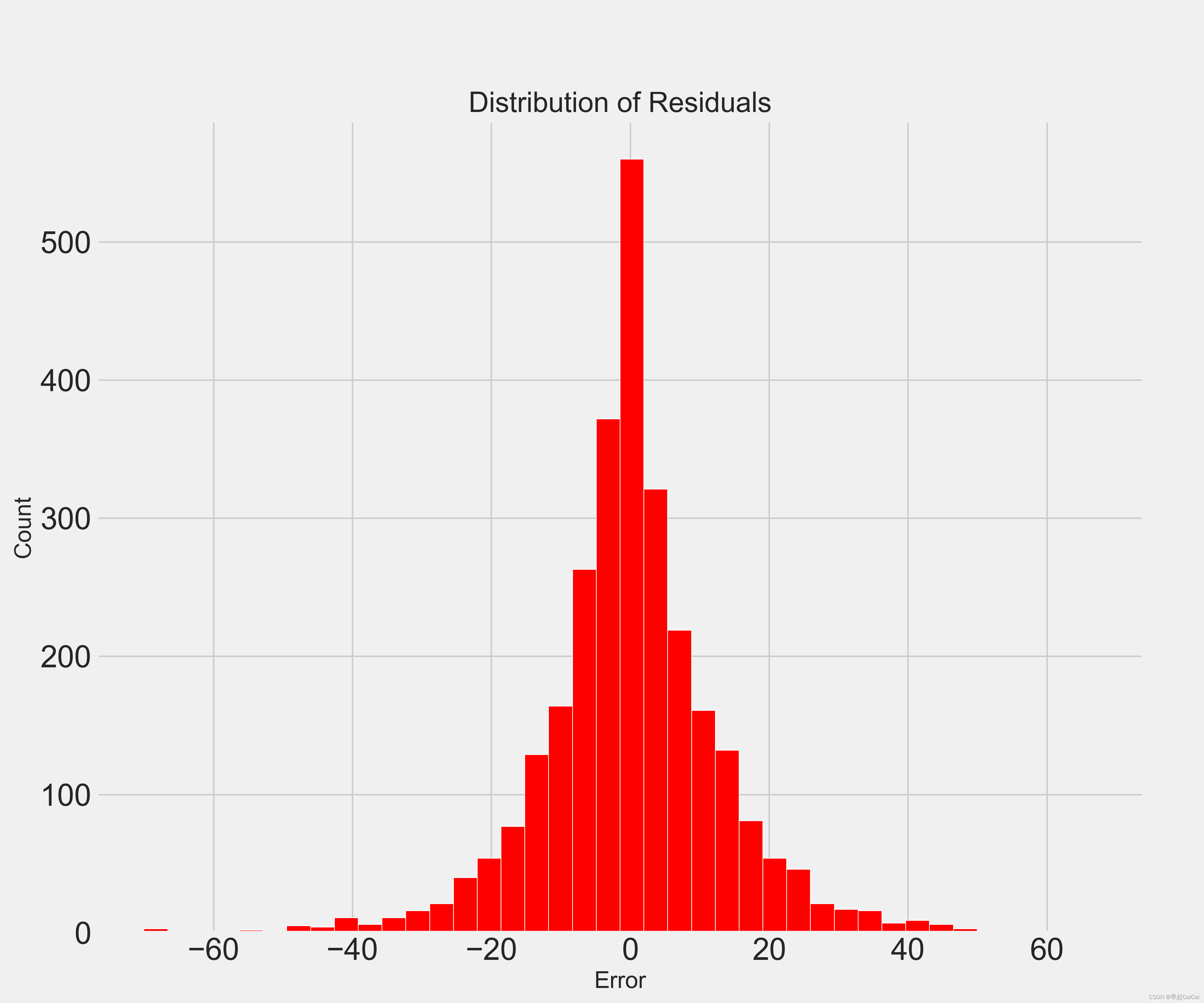
残差分布

residuals = final_pred - y_test
plt.hist(residuals, color = 'red', bins = 40, edgecolor = 'white')
plt.xlabel('Error'); plt.ylabel('Count')
plt.title("Distribution of Residuals")

Reference

机器学习项目实战-能源利用率 Part-1（数据清洗）

机器学习项目实战-能源利用率 Part-2（探索性数据分析）

机器学习项目实战-能源利用率 Part-3（特征工程与特征筛选）

机器学习项目实战-能源利用率2-建模