这道题真是写的我想吐了，主要是函数太多，排错太难了，搞了两个小时，基本就是在排错，排了一个小时，后面自己心态也有点崩溃了，其实不是一道很难的题，但是是一个非常麻烦的题目，但是再麻烦的题目我现在已经做出来了，那就一起来盘一盘它吧，要不然过了几天就又白盘了，就忘的九霄云外去了。

1.如何建立一个搜索二叉树？

1.规定结构体，以及规定结构体指针（不然指针容易晕）

typedef struct TreeNode *Tree;
struct TreeNode{
    int v;
    Tree Left , Right;
    int flag;
};

有个问题：就是为啥这上面的这个结构体都没有定义。然而下面可以把它当做已经定义好的使用？

2. 初始化二叉树单个节点，属于是将这些琐碎的操作封装了。（java呵呵呵）

Tree newTreeNode(int v){
    Tree T = (Tree)malloc(sizeof(struct TreeNode));
    T -> v = v;
    T -> Left = NULL;
    T -> Right = NULL;
    T -> flag = 0;
    return T;
}

3.插入操作，向二叉搜索树插入数据，这里需要注意的是，这是二叉搜索树，所以我们不仅需要递归到要插入节点相应的位置还要判断此时要插入的这个节点到底比现在的节点小还是大。

//向已经建好的树插入数据
Tree insert(Tree T, int V){
    //如果这个节点开始个控节点就直接插入即可，
    //否则就执行下面的逻辑直到找到自己的位置再插入
    if(!T) T =  newTreeNode(V);
    if(T -> v > V) T->Left = insert( T->Left , V);
    if(T -> v < V) T->Right = insert( T->Right , V);
    return T;
}

 4.最后一步，建立二叉树，初始化完树的根结点，之后的操作就是调用刚才我们定义好的插入操作，将题目中输入的样例一个一个插入进去。

//建立新树
Tree createTree(int N){
    int v;
    cin>>v;
    Tree T = newTreeNode(v);
    for(int i=0 ; i<(N-1) ; i++){
        cin>>v;
        // cout<<v<<endl;
        T = insert(T,v);
    }
    return T;
}

2.如何判别两个二叉搜索树是否一样

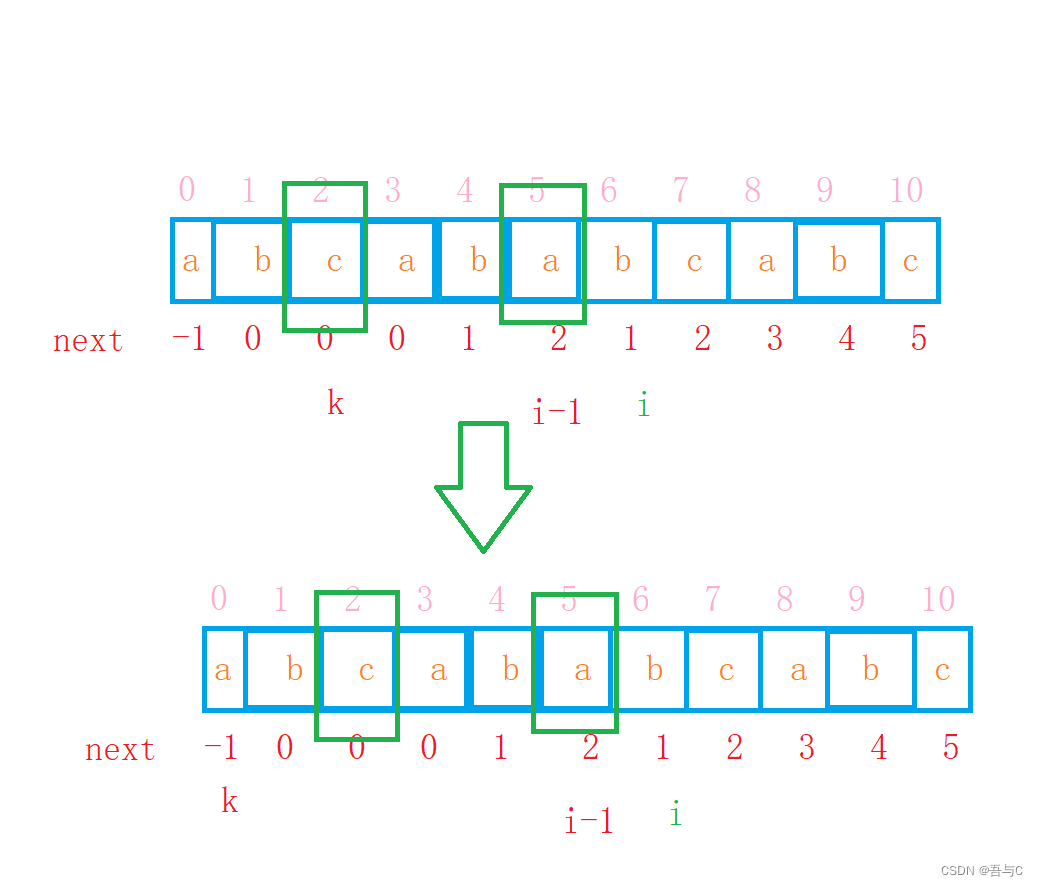
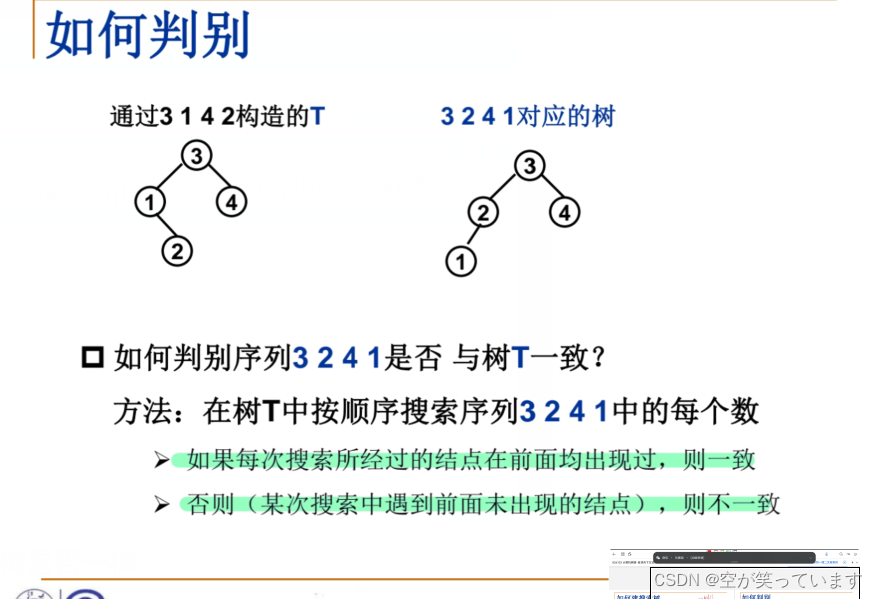
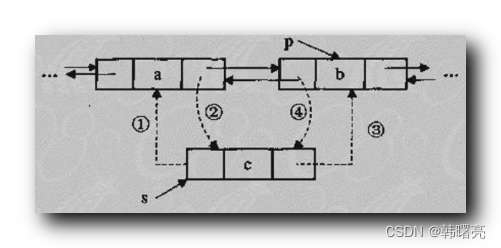
  1. 其实如何判断两个二叉树是否一样的问题，我们有很多种解法，但最终我们需要一种比较简单容易实现的方法，因为毕竟我们这是在写题目而不是在搞工程，所以我选择只建立一个树。再遍历其他树的时候，我们一个节点节点判断，采取下面图片这种方法，为啥可以这么判断，看代码

//搜索的顺序和插入的时候一样
int check(Tree T , int V){
    if(T->flag){
        if(V > T->v ) return check( T->Right , V);
            else if(V < T->v ) return check( T->Left , V);
			else return 0;
    }
    else{
        
            if(V == T->v) {
               T -> flag = 1;
                return 1;
            }
			else {
                // cout<<"what"<<endl;
                return 0;
            }
            
    }
}

你有没有发现插入和搜索的代码当我们如果将搜索的操作改为插入那将一模一样，所以说如果在原先建立的二叉搜索树中搜索某个节点的时候，这个节点按照我们搜索的步骤找到了自己应该处于的位置(和插入时一样)。但是发现这个位置的节点和自己不一样，那么就可以判断这两个二叉搜索建出来的树一定不一样。

  2.然后上面的是搜索一个节点的代码，但是我们需要搜索的节点可不止有一个，而是一颗完整的树，所以需要在外面再套层壳子。

int Judge(Tree T, int N){
    int V , i;
    cin>>V;
    int flag = 1;
    if( V!=T->v ){
        flag = 0;
    }else{
		T ->flag =1;
	}

    //为啥设为1，头结点遍历过了。
    for(i=1 ; i<N ; i++){
		cin>>V;
        // cout<<"V:"<<V<<endl;
        if((!check(T,V))&&(flag)){ 
			flag = 0;
		}
    }
    return flag;
}

这里一定要注意的点是，我们在输入下一个搜索二叉树的样例的时候我们一定要将原先那个正在判断的二叉树读完，所以我们这两个地方千万不能像我这样写,因为如果像我这样写就会产生一种情况，我们没有读完原先那个二叉搜索树的样例，使得我们的样例被输入到了其他的变量中，那就会产生我们想象不到的结果。

if( V!=T->v ){
        return 0;
    }else{
		T ->flag =1;
	}

if((!check(T,V))&&(flag)){ 
			return 0;
		}

 至此，这道题讲解完毕，下面是完整的正确代码:

#include <cstddef>
#include <iostream>
using namespace std;


typedef struct TreeNode *Tree;
struct TreeNode{
    int v;
    Tree Left , Right;
    int flag;
};

//和java一样new一个节点
Tree newTreeNode(int v){
    Tree T = (Tree)malloc(sizeof(struct TreeNode));
    T -> v = v;
    T -> Left = NULL;
    T -> Right = NULL;
    T -> flag = 0;
    return T;
}
//向已经建好的树插入数据
Tree insert(Tree T, int V){
    //如果这个节点开始个控节点就直接插入即可，
    //否则就执行下面的逻辑直到找到自己的位置再插入
    if(!T) T =  newTreeNode(V);
    if(T -> v > V) T->Left = insert( T->Left , V);
    if(T -> v < V) T->Right = insert( T->Right , V);
    return T;
}
//建立新树
Tree createTree(int N){
    int v;
    cin>>v;
    Tree T = newTreeNode(v);
    for(int i=0 ; i<(N-1) ; i++){
        cin>>v;
        // cout<<v<<endl;
        T = insert(T,v);
    }
    return T;
}
//遍历的方法和插入的时候一样
int check(Tree T , int V){
    if(T->flag){
        if(V > T->v ) return check( T->Right , V);
            else if(V < T->v ) return check( T->Left , V);
			else return 0;
    }
    else{
        
            if(V == T->v) {
               T -> flag = 1;
                return 1;
            }
			else {
                // cout<<"what"<<endl;
                return 0;
            }
            
    }
}
//判断思路:遍历一遍后面来比较的树，看遍历顺序是否对的上，如果对得上，那么就是同一颗树
//遍历的方法和插入的时候一样。
int Judge(Tree T, int N){
    int V , i;
    cin>>V;
    int flag = 1;
    if( V!=T->v ){
        flag = 0;
    }else{
		T ->flag =1;
	}

    //为啥设为1，头结点遍历过了。
    for(i=1 ; i<N ; i++){
		cin>>V;
        // cout<<"V:"<<V<<endl;
        if((!check(T,V))&&(flag)){ 
			flag = 0;
		}
    }
    return flag;
}


void ResetT(Tree T){
    if(T == NULL) return;
    T -> flag = 0;
    if(T->Left != NULL) ResetT(T->Left);
    if(T->Right != NULL) ResetT(T->Right);
    return;
}

int main(){
    int N,L;
    scanf("%d",&N);
    while(N){
        cin>>L;
        Tree T = createTree(N);
        for(int i=0 ;i<L; i++){

        if(Judge(T,N)) {
            printf("Yes\n");
        }
        else {
            printf("No\n");
        }
        ResetT(T);
        }
        T = NULL;
        scanf("%d",&N);
    }
    return 0;
    
}